【学习笔记】2、逻辑代数与硬件描述语言基础
2.1 逻辑代数
(1)逻辑代数的基本定律和恒等式
| 基本定律 | 或 “+” | 与 “·” | 非 “—” |
|---|---|---|---|
| 0-1律 | A+0=A A+1=1 A+A=A A+ A  ̄ \overline{A} A=1(互补律) | A·0=0 A·1=A A·A=A A· A  ̄ \overline{A} A=0 | A  ̄  ̄ \overline{\overline{A}} A=A |
| 结合律 | (A+B)+C = A+(B+C) | (AB)C=A(BC)=ABC | |
| 交换律 | A+B = B+A | AB=BA | |
| 分配律 | A(B+C) = AB+AC | A+BC = (A+B)(A+C) | |
| 反演律(摩根定理) |
A
?
B
?
C
?
.
.
.
 ̄
\overline{A·B·C·...}
A?B?C?... =
A
 ̄
\overline{A}
A+
B
 ̄
\overline{B}
B+
C
 ̄
\overline{C}
C+… A ? B  ̄ \overline{A·B} A?B = A  ̄ \overline{A} A+ B  ̄ \overline{B} B |
A
+
B
+
C
+
.
.
.
 ̄
\overline{A+B+C+...}
A+B+C+...? =
A
 ̄
\overline{A}
A·
B
 ̄
\overline{B}
B·
C
 ̄
\overline{C}
C·… A + B  ̄ \overline{A+B} A+B? = A  ̄ \overline{A} A· B  ̄ \overline{B} B | |
| 吸收律 | A + A · B = A A · (A + B) = A A + A  ̄ \overline{A} A · B = A + B (A + B) · (A + C) = A + BC | ||
| 常用恒等式 | AB + A  ̄ \overline{A} AC + BC = AB + A  ̄ \overline{A} AC | AB+ A  ̄ \overline{A} AC+BCD = AB + A  ̄ \overline{A} AC |
- 反演律,被称为“摩根定理”。(1)用于求一个原函数的非函数(2)对逻辑函数进行变换。
- 可以通过列出真值表的方式证明等式的成立。
- 常用恒等式 AB +
A
 ̄
\overline{A}
AC + BC = AB +
A
 ̄
\overline{A}
AC 的证明过程如下:
AB + A  ̄ \overline{A} AC + BC = AB + A  ̄ \overline{A} AC + (A + A  ̄ \overline{A} A)BC =AB + A  ̄ \overline{A} AC + ABC + A  ̄ \overline{A} ABC = AB(1+C) + A  ̄ \overline{A} AC(1+B) = AB+ A  ̄ \overline{A} AC - 上述常用恒等式说明:若两个乘积项中分别包含A和 A  ̄ \overline{A} A,而这两个乘积项的其余因子组成第三个乘积项时,则第三个乘积项是多余的,可以消去。
(2)逻辑代数的基本规则
代入规则
- 等式两边存在某变量A,可以用一个函数代替A,代入等式。
- 代入规则适合所有基本定律或定理的应用范围。
| 原等式 L | 代入的函数 | 代入后 |
|---|---|---|
| B (A+C) = BA +BC | E+F | B( (E+F) +C) = B(E+F)+BC |
| A B  ̄ \overline{AB} AB = A  ̄ \overline{A} A + B  ̄ \overline{B} B | L = CD | ( C D ) B  ̄ \overline{(CD)B} (CD)B? = C D  ̄ \overline{CD} CD + B  ̄ \overline{B} B = C  ̄ \overline{C} C+ D  ̄ \overline{D} D+ B  ̄ \overline{B} B |
反演规则
- 原函数L
- 将原函数中的 与(·) 换成 或(+)
- 将原函数中的 或(+) 换成 与(·)
- 将原函数中的 原变量A 换成 非变量 A  ̄ \overline{A} A
- 将原函数中的 非变量 A  ̄ \overline{A} A 换成 原变量A
- 得到非函数 L  ̄ \overline{L} L
| 原函数L | 非函数 L  ̄ \overline{L} L |
|---|---|
| L = A B  ̄ \overline{AB} AB + CD + 0 | L  ̄ \overline{L} L = (A+B)·( C  ̄ \overline{C} C+ D  ̄ \overline{D} D)· 1 = (A+B)·( C  ̄ \overline{C} C+ D  ̄ \overline{D} D) |
| L = A + B C  ̄ + D + E  ̄  ̄  ̄ \overline{B\overline{C} + \overline{D + \overline{E}}} BC+D+E?? | L  ̄ \overline{L} L = A  ̄ \overline{A} A · ( B  ̄ + C ) + D  ̄ ? E  ̄  ̄ \overline{(\overline{B}+C) + \overline{\overline{D} · E}} (B+C)+D?E?) |
对偶规则
- 与反演规则不同,无需将 变量A 变为 非变量 A  ̄ \overline{A} A
- 变换时,注意保持 “先括号,然后与,最后或”的运算顺序。
- 原函数L
- 将原函数中的 与(·) 换成 或(+)
- 将原函数中的 或(+) 换成 与(·)
- 1换成0
- 0换成1
- 对偶式L’
| 原函数L | 对偶式L’ |
|---|---|
| L = (A+ B  ̄ \overline{B} B )(A+C) | L’ = A B  ̄ \overline{B} B +AC |
| 吸收律 A+ A  ̄ \overline{A} AB = A+B | A·( A  ̄ \overline{A} A+B) = A·B |
(3)逻辑函数的代数化简法
化简逻辑函数,节省逻辑电路的器件。
最简 与-或 表达式(积之和)
- 与(逻辑乘),把变量连接起来。与项,乘积项。
- 或运算,将乘积项连接起来。
- 定义:若干个逻辑关系相同的“与-或表达式”中,包含的与项数最少,每个与项中变量最少的表达式,称为“最简 与-或 表达式”。
| 与-或表达式 | 与非-与非 表达式 | 或 - 与 表达式 | 或非-或非表达式 | 与-或非表达式 |
|---|---|---|---|---|
| L = AC + C  ̄ \overline{C} CD | L = A C  ̄ ? C  ̄ D  ̄  ̄ \overline{\overline{AC} · \overline{\overline{C}D}} AC?CD | L = (A+ C  ̄ \overline{C} C)(C+D) | L = ( A + C  ̄ )  ̄ + ( C + D )  ̄  ̄ \overline{\overline{ (A+\overline{C}) }+\overline{( C + D )}} (A+C)?+(C+D)?? | L = A  ̄ C + C  ̄ ? D  ̄  ̄ \overline{ \overline{A}C + \overline{C}·\overline{D}} AC+C?D? |
L = AC +
C
 ̄
\overline{C}
CD
=
A
C
+
C
 ̄
D
 ̄
 ̄
\overline{\overline{ AC + \overline{C}D}}
AC+CD??
= 反演律
A
C
 ̄
?
C
 ̄
D
 ̄
 ̄
\overline{\overline{AC} · \overline{\overline{C}D}}
AC?CD
L = AC+
C
 ̄
\overline{C}
CD
= 吸收律 (AC + ACD) + 吸收律(
C
 ̄
\overline{C}
CD +
C
 ̄
\overline{C}
CDA)
= 交换结合律/常用恒等式 AC+
C
 ̄
\overline{C}
CD + AD· (C+
C
 ̄
\overline{C}
C)
= 0-1律 AC+
C
 ̄
\overline{C}
CD + AD· 1
= 0-1律 AC +
C
 ̄
\overline{C}
CD +AD +0
= 0-1律 AC +
C
 ̄
\overline{C}
CD +AD +
C
 ̄
\overline{C}
CC
=结合律 (A+
C
 ̄
\overline{C}
C) ( C + D )
L = AC +
C
 ̄
\overline{C}
CD = (A+
C
 ̄
\overline{C}
C) ( C + D )
=
(
A
+
C
 ̄
)
(
C
+
D
)
 ̄
 ̄
\overline{\overline{ (A+\overline{C}) ( C + D )}}
(A+C)(C+D)??
= 反演律
(
A
+
C
 ̄
)
 ̄
+
(
C
+
D
)
 ̄
 ̄
\overline{\overline{ (A+\overline{C}) }+\overline{( C + D )}}
(A+C)?+(C+D)??
= 反演律
A
 ̄
C
+
C
 ̄
?
D
 ̄
 ̄
\overline{ \overline{A}C + \overline{C}·\overline{D}}
AC+C?D?
逻辑函数的化简方法
-
代数法。运用逻辑代数的基本定律和恒等式对逻辑函数进行化简
-
代数法 - 并项法
利用 A+ A  ̄ \overline{A} A = 1。
L 1 = A B C + A B C  ̄ = A B ( C + C  ̄ ) = A B L_1 = ABC + AB\overline{C} = AB(C+\overline{C}) = AB L1?=ABC+ABC=AB(C+C)=AB -
代数法 - 吸收法
利用A+AB=A。
L = A  ̄ \overline{A} AB + A  ̄ \overline{A} ABCDE+ A  ̄ \overline{A} ABCDF = A  ̄ \overline{A} AB -
代数法 - 消去法
利用A+ A  ̄ \overline{A} AB = A+B。
L = AB + A  ̄ \overline{A} AC + B  ̄ \overline{B} BC
= AB + ( A  ̄ \overline{A} A + B  ̄ \overline{B} B)C
= AB + A B  ̄ \overline{AB} AB C
= AB + C -
代数法 - 配项法(要有一定的经验,否则越配越繁)
利用A=A(B+ B  ̄ \overline{B} B)
L= AB+ A  ̄ \overline{A} A· C  ̄ \overline{C} C + B · C  ̄ \overline{C} C
= AB + A  ̄ \overline{A} A· C  ̄ \overline{C} C + (A+ A  ̄ \overline{A} A·)B · C  ̄ \overline{C} C
= AB + A  ̄ \overline{A} A· C  ̄ \overline{C} C + AB C  ̄ \overline{C} C + A  ̄ \overline{A} AB C  ̄ \overline{C} C
= (AB+AB C  ̄ \overline{C} C ) + ( A  ̄ \overline{A} A· C  ̄ \overline{C} C + A  ̄ \overline{A} A· C  ̄ \overline{C} C B)
= AB + A  ̄ \overline{A} A· C  ̄ \overline{C} C
2.2 逻辑函数的卡诺图化简法
利用卡诺图法,得到最简的逻辑表达式。
(1)最小项的定义以及性质
- 定义:
(1)n个变量的最小项,是n个因子的乘积。每个变量因子都以原变量或者非变量的形式在乘积项中出现,且仅出现一次。
(2)A,B,C三个变量的最小项有 2 3 = 8 2^3=8 23=8个,(0 = 0b000) A  ̄ \overline{A} A· B  ̄ \overline{B} B· C  ̄ \overline{C} C,(1 = 0b001) A  ̄ \overline{A} A· B  ̄ \overline{B} B·C,(2 = 0b010) A  ̄ \overline{A} A·B· C  ̄ \overline{C} C,(3 = 0b011) A  ̄ \overline{A} A·BC,(4 = 0b100)A· B  ̄ \overline{B} B· C  ̄ \overline{C} C,(5 = 0b101)A· B  ̄ \overline{B} B·C,(6 = 0b110)AB· C  ̄ \overline{C} C,(7 = 0b111)ABC
| A | B | C | A  ̄ \overline{A} A· B  ̄ \overline{B} B· C  ̄ \overline{C} C | A  ̄ \overline{A} A· B  ̄ \overline{B} B·C | A  ̄ \overline{A} A·B· C  ̄ \overline{C} C | A  ̄ \overline{A} A·BC | A· B  ̄ \overline{B} B· C  ̄ \overline{C} C | A· B  ̄ \overline{B} B·C | AB· C  ̄ \overline{C} C | ABC |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
-
性质:
(1)输入变量取一组值,在所有的最小项中,只会有一组最小项值为1。
(2)不同的最小项,使它值为1的输入变量的取值 是不同的。
(3)输入变量取一组值,任意两个最小项的乘积为0。
(4)输入变量取一组值,所有最小项之和为1。 -
最小项的编号:
(1) m 0 m_0 m0? : (0 = 0b000) A  ̄ \overline{A} A· B  ̄ \overline{B} B· C  ̄ \overline{C} C
(2) m 1 m_1 m1? : (1 = 0b001) A  ̄ \overline{A} A· B  ̄ \overline{B} B·C
(3) m 2 m_2 m2? : (2 = 0b010) A  ̄ \overline{A} A·B· C  ̄ \overline{C} C
(4) m 3 m_3 m3? : (3 = 0b011) A  ̄ \overline{A} A·BC
(5) m 4 m_4 m4? : (4 = 0b100)A· B  ̄ \overline{B} B· C  ̄ \overline{C} C
(6) m 5 m_5 m5? : (5 = 0b101)A· B  ̄ \overline{B} B·C
(7) m 6 m_6 m6? : (6 = 0b110)AB· C  ̄ \overline{C} C
(8) m 7 m_7 m7? : (7 = 0b111)ABC
(2)逻辑函数的最小项表达式
-
最小项表达式:逻辑函数L = 若干个最小项之和
-
L(A,B,C) = AB + A  ̄ \overline{A} AC 不是最小项表达式
L(A,B,C) = AB + A  ̄ \overline{A} AC = AB(C+ C  ̄ \overline{C} C) + A  ̄ \overline{A} A(B+ B  ̄ \overline{B} B)C = ABC + AB C  ̄ \overline{C} C + A  ̄ \overline{A} ABC + A  ̄ \overline{A} A· B  ̄ \overline{B} BC -
L(A,B,C) = m 7 m_7 m7? + m 6 m_6 m6? + m 3 m_3 m3? + m 1 m_1 m1? = ∑ m ( 1 , 3 , 6 , 7 ) \sum m(1,3,6,7) ∑m(1,3,6,7)
-
任意一个逻辑函数,经过变换,都能表示成 唯一的最小项表达式。
(3)用卡诺图表示逻辑函数
- 将逻辑函数的最小项表达式中的各个最小项,对应地填入特定的方格中。
- 卡诺图是逻辑函数的图形表示。
1个变量D 的卡诺图
2
1
2^1
21=2 个最小项(
m
0
m_0
m0?=
D
 ̄
\overline{D}
D和
m
1
m_1
m1?=D)。
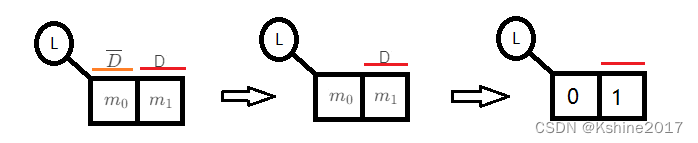
2个变量C和D 的卡诺图
“折叠展开” 法则,如下图所示。
2
2
2^2
22=4 个最小项(
m
0
m_0
m0?=
C
 ̄
\overline{C}
C·
D
 ̄
\overline{D}
D和
m
1
m_1
m1?=
C
 ̄
\overline{C}
C·D和
m
2
m_2
m2?= C·
D
 ̄
\overline{D}
D和
m
3
m_3
m3?= C·D)。
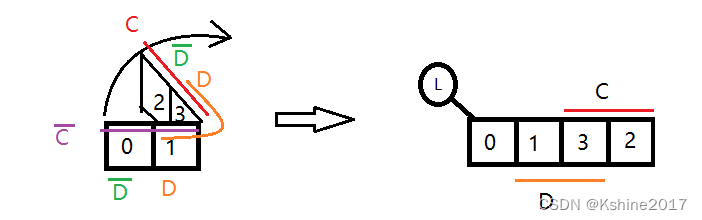
3个变量B和C和D的卡诺图
“折叠展开” 法则,如下图所示。
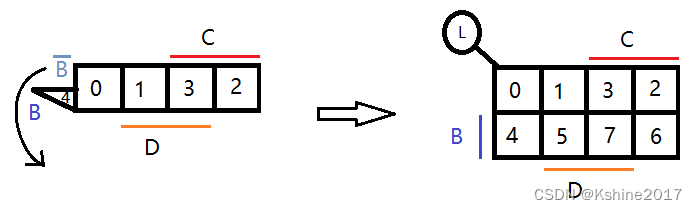
4个变量A和B和C和D的卡诺图

-
卡诺图的特点:循环邻接
(1)各个小方格对应的各变量不同的组合。
(2)一个格子与上下左右相邻的格子只有一个因子的差异
(3)边界最上与最小,边界最左与最右,4个对角格子上下左右满足相邻(斜对角不相邻),一个因子的差异。 -
举例画卡诺图:
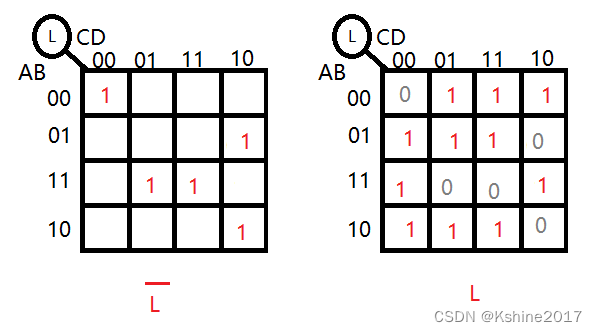
(1)L(A,B,C,D) = ∑ m ( 0 , 1 , 2 , 3 , 4 , 8 , 10 , 11 , 14 , 15 ) \sum m(0,1,2,3,4,8,10,11,14,15) ∑m(0,1,2,3,4,8,10,11,14,15) ,存在的最小项,在对应的卡诺图格子中填1,不存在的最小项,在格子中填0
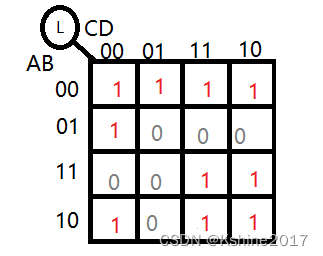
(2)L(A,B,C,D) = ( A  ̄ \overline{A} A+ B  ̄ \overline{B} B+ C  ̄ \overline{C} C+ D  ̄ \overline{D} D) ( A  ̄ \overline{A} A+ B  ̄ \overline{B} B+C+ D  ̄ \overline{D} D) ( A  ̄ \overline{A} A+B+ C  ̄ \overline{C} C+D) (A+ B  ̄ \overline{B} B+ C  ̄ \overline{C} C+D) (A+B+C+D)
反演律(摩根定理) L  ̄ \overline{L} L= ABCD + AB· C  ̄ \overline{C} CD + A B  ̄ \overline{B} B·C· D  ̄ \overline{D} D + A  ̄ \overline{A} A·BC· D  ̄ \overline{D} D + A  ̄ \overline{A} A· B  ̄ \overline{B} B· C  ̄ \overline{C} C· D  ̄ \overline{D} D = ∑ m ( 15 , 13 , 10 , 6 , 0 ) \sum m(15,13,10,6,0) ∑m(15,13,10,6,0)
(4)用卡诺图化简逻辑函数
化简的依据
(1)根据“循环邻接”的特性(上下左右)。
(2)两个相邻的方格为1,他们的和将消去一个变量。如:(
m
15
=
1111
m_{15} =1111
m15?=1111)ABCD + (
m
14
=
1110
m_{14} = 1110
m14?=1110)ABC
D
 ̄
\overline{D}
D = ABC
(3)四个相邻的方格为1,他们的和将消去两个变量。如 (
m
2
=
0010
m_{2} =0010
m2?=0010)
A
 ̄
?
B
 ̄
?
C
?
D
 ̄
\overline{A}· \overline{B}· C· \overline{D}
A?B?C?D + (
m
3
=
0011
m_{3} =0011
m3?=0011)
A
 ̄
?
B
 ̄
?
C
?
D
\overline{A}· \overline{B}· C· D
A?B?C?D + (
m
6
=
0110
m_{6} =0110
m6?=0110)
A
 ̄
?
B
?
C
?
D
 ̄
\overline{A}· B· C· \overline{D}
A?B?C?D + (
m
7
=
0111
m_{7} =0111
m7?=0111)
A
 ̄
?
B
?
C
?
D
\overline{A}· B· C· D
A?B?C?D =
A
 ̄
?
C
\overline{A}· C
A?C

化简的步骤
(1)将逻辑函数"L" 写成最小项表达式。
(2)填写卡诺图,存在的最小项在表格中填写1,其余方格填0。
(3)合并最小项。相邻的1方格 圈成一组(包围圈,虚线框)。每组包含
2
n
2^n
2n个方格。每个包围圈写成一个新的乘积项。可重复包围。
(4)将所有的包围圈对应的乘积项相加。
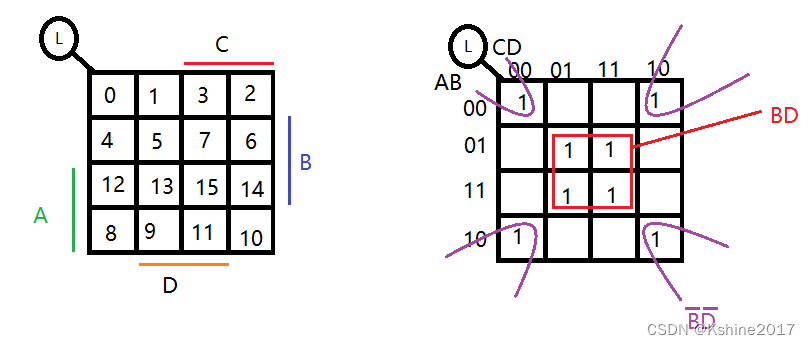
L (A,B,C,D) =
∑
m
(
0
,
2
,
5
,
7
,
8
,
10
,
13
,
15
)
\sum m(0,2,5,7,8,10,13,15)
∑m(0,2,5,7,8,10,13,15) = B·D+
B
 ̄
\overline{B}
B·
D
 ̄
\overline{D}
D
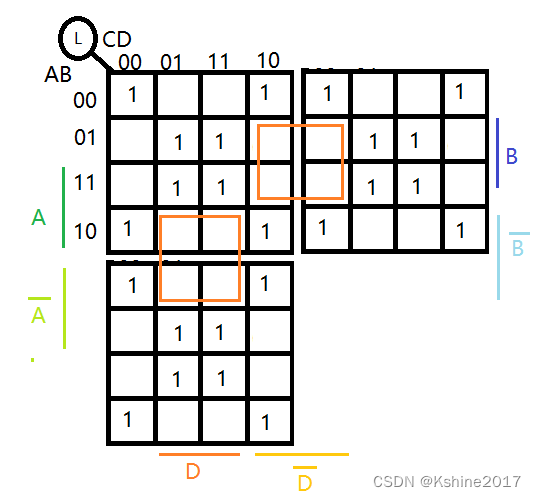
- 很多情况可以圈0,得到的是化简式的非,即“
L
 ̄
\overline{L}
L”
L  ̄ \overline{L} L = B  ̄ \overline{B} BD+B D  ̄ \overline{D} D
L = B  ̄ D + B D  ̄  ̄ \overline{\overline{B}D+B\overline{D}} BD+BD? =( B+ D  ̄ \overline{D} D) ( B  ̄ \overline{B} B+D) = B·D+ B  ̄ \overline{B} B· D  ̄ \overline{D} D
- 本章节最重要的注意点 – 将真值表转化为卡诺图,可以得到逻辑函数。
(1)实际应用中,可以确定输入变量的个数以及状态。可以确定输出的结果。
(2)列出真值表。
(3)根据真值表,填写卡诺图。
(4)进行卡诺图化简,得到逻辑函数(化简后的最小项表达式)。
(5)进行逻辑电路的设计与实现。
例如:真值表
| m 0 ? 15 m_{0-15} m0?15? | A | B | C | D | L |
|---|---|---|---|---|---|
| m 0 m_{0} m0? | 0 | 0 | 0 | 0 | 1 |
| m 1 m_{1} m1? | 0 | 0 | 0 | 1 | 0 |
| m 2 m_{2} m2? | 0 | 0 | 1 | 0 | 0 |
| m 3 m_{3} m3? | 0 | 0 | 1 | 1 | 0 |
| m 4 m_{4} m4? | 0 | 1 | 0 | 0 | 1 |
| m 5 m_{5} m5? | 0 | 1 | 0 | 1 | 1 |
| m 6 m_{6} m6? | 0 | 1 | 1 | 0 | 0 |
| m 7 m_{7} m7? | 0 | 1 | 1 | 1 | 0 |
| m 8 m_{8} m8? | 1 | 0 | 0 | 0 | 1 |
| m 9 m_{9} m9? | 1 | 0 | 0 | 1 | 0 |
| m 10 m_{10} m10? | 1 | 0 | 1 | 0 | 1 |
| m 11 m_{11} m11? | 1 | 0 | 1 | 1 | 0 |
| m 12 m_{12} m12? | 1 | 1 | 0 | 0 | 1 |
| m 13 m_{13} m13? | 1 | 1 | 0 | 1 | 0 |
| m 14 m_{14} m14? | 1 | 1 | 1 | 0 | 0 |
| m 15 m_{15} m15? | 1 | 1 | 1 | 1 | 1 |
卡诺图
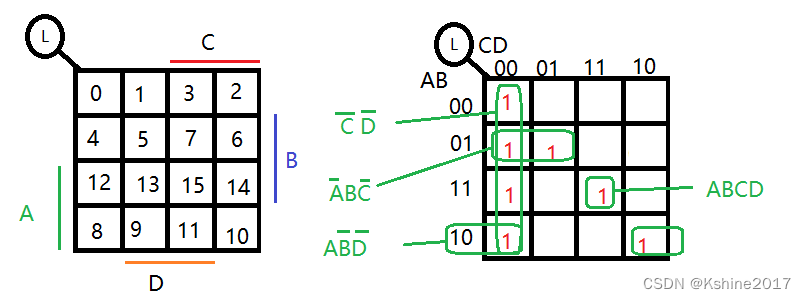
逻辑函数
L =
C
 ̄
\overline{C}
C·
D
 ̄
\overline{D}
D + A
B
 ̄
\overline{B}
B·
D
 ̄
\overline{D}
D +
A
 ̄
\overline{A}
AB
C
 ̄
\overline{C}
C + ABCD
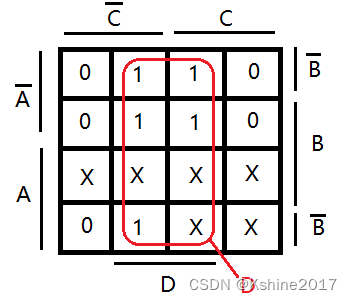
具有无关项的化简
(1)在真值表内,对应于变量的某些取值下,函数L的值可以是任意的。或者这些变量的取值根本不会出现。这些变量取值所对应的最小项称为无关项或任意项。
(2)在卡诺图中,无关项的意义是,它的值X可以是0或者1。
| 对应十进制数 | 变量A | 变量B | 变量C | 变量D | 输出L (奇数1,偶数0) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 无关项 | 1 | 0 | 1 | 0 | X |
| 无关项 | 1 | 0 | 1 | 1 | X |
| 无关项 | 1 | 1 | 0 | 0 | X |
| 无关项 | 1 | 1 | 0 | 1 | X |
| 无关项 | 1 | 1 | 1 | 0 | X |
| 无关项 | 1 | 1 | 1 | 1 | X |
根据卡诺图,可以得出
L
=
D
L = D
L=D
包围圈 覆盖了 正负A,正负B,正负C,正D。
2.3 硬件描述语言 Verilog HDL 基础
- 硬件描述语言Verilog HDL 类似于高级程序设计语言(C语言等等)。
- 一种以文本形式来描述数字系统硬件的结构和行为的语言。
- 计算机对于HDL的处理包括:逻辑仿真和逻辑综合。
- 逻辑仿真:计算机软件对数字逻辑电路的结构和行为进行预测。以文本形式或者时序波形的形式给出电路的输出。
- 逻辑综合:从HDL描述的数字逻辑电路模型中,导出电路基本元器件列表以及元器件之间的连接关系(门级网表)。
- 硬件描述语言的发展:早期的ABEL -> 目前的 VHDL(美国国防部)和Verilog(Cadence收购的一家公司) 。
- Verilog 更容易学习和使用。
(1)Verlog的基本语法规则
间隔符
空格符 \b
Tab键 \t
换行符 \n
注释符
/* 注释1 */
//注释2
标识符和关键词
- 标志符:给对象取名。使用英文字母,数字,“$”和下划线“_”。必须以英文字母或者下划线开始。区分英文大小写。
- 关键字:通常为小写的英文字符串。不能作为标识符使用。
module
endmodule
input
output
wire
reg
and
等等
逻辑值集合
- 四种基本的逻辑值
| 值 | 含义 |
|---|---|
| 0 | 逻辑0,逻辑假 |
| 1 | 逻辑1,逻辑真 |
| x 或 X | 不确定的值(未知状态) |
| z 或 Z | 高阻态 |
常量及其表示
- 程序运行过程中,不能改变数值的量,称为常量。
- 整数型常量
<+/-> <位宽> ' <基数符号> <数值>
(1)<+/-> 正负号,当常量为正整数时,可以省略正号不写。
(2)<位宽> 二进制数的宽度
(3)<基数符号> 后面数值的表示形式。b或者B表示后面的数值是二进制数。d或者D表示后面的数值是十进制数。h或者H表示后面的数值是十六进制数。o或者O表示后面的数值是八进制数。
(4)可以在数字之间增加下划线,增加可读性。
3'b101
5'o37
8'he3
-4'd10
4'b1x0x
8'b1001_0011
- 实数型常量
(1)两种表示方法,简单的十进制记数法;科学记数法。
0.01
2.0
4.56
23_5.1E2 = 23 510.0
3.6E2 = 360.0
5E-4 = 0.0005
- 使用标识符代表一个常量,称为符号常量
parameter 参数名1 = 常数表达式 , 参数名2 = 常量表达式2 , ... ;
parameter BIT = 1 , BYTE = 8 , PI = 3.14;
parameter DELAY = (BYTE + BIT)/2;
字符串
- 双引号" " 内部的字符序列。
- 不允许多行书写
"ab" = 16'h5758
(2)变量的数据类型
- 与常量不同,程序运行过程中,值可以改变,称为变量。
- verilog中有两种变量:线网类型,寄存器类型。
线网类型 net type
- 线网类型是硬件电路中元器件之间实际连线的抽象。
- 线网类型变量的值由驱动元件的值决定。
- 如下图所示,L就是一个线网类型的变量。
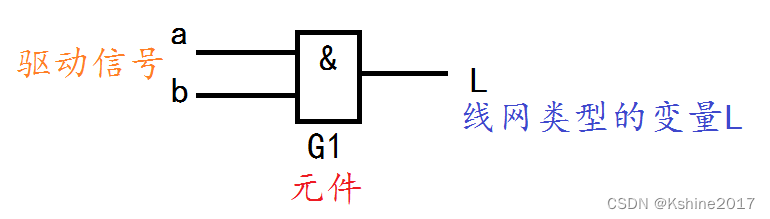
wire a,b; //声明两个线网变量a和b (上图中的a和b), 默认是一位位宽
wrie L; //声明线网变量L ,默认是一位位宽
- 线网类型关键字包括
wire
wand
wor
tri
triand
trior
trireg
等等
-
线网类型变量被定义后,如果没有驱动元件驱动,则线网类型变量处于默认值,“高阻态”z。
-
线网trireg变量的默认值是x
-
线网类型的关键字是wire。默认是一位位宽。
wire[ n-1 : 0 ] 变量名1,变量名2,变量名3, ... ,变量名m ;
wire [7:0] databus;//声明定义一个 8位宽的 变量databus。(总线)
wire[32:1] busA,busB,busC;//3个位宽为32的线网变量(总线)
寄存器类型 register type
- 寄存器类型是数据存储单元的抽象。
- 寄存器类型变量具有状态保持的作用。
- 寄存器型变量只能在initial或always内部被赋值。
- 寄存器型变量在没有被赋值时默认值是x。
| 寄存器类型 | 功能说明 |
|---|---|
| reg | 用于行为描述中对寄存器型变量的说明(默认位宽为1) |
| integer | 32位带符号的整数型变量 |
| real | 64位带符号的实数型变量,默认为0 |
| time | 64位无符号的时间型变量 |
- reg
reg[ n-1 :0 ] 变量名1, 变量名2, 变量名3, ... ,变量名n;
reg clock;//定义1位寄存器变量
reg[3:0] counter;//定义4位寄存器变量
- integer、real、time 纯数学的抽象描述
- initial是一个过程语句结构
integer counter;//定义一个整型变量
initial
counter = -1;//将-1以补码的形式存储在counter中
- real型变量,用于对实数型常量进行存储和运算。实数不能定义范围,其默认值为0。实数值被赋值赋值给一个integer型变量时,只保留整数部分的值。
real delta;
initial
begin
delta = 4e10;//给delta赋值
delta = 2.13;
end
integer i;//定义一个整型变量i;
initial
i = delta;//i 得到的值是2(只将实数2.13的整数部分赋值给i)
- time型变量,存储仿真时间,无符号数。
- 调用$time可以得到当前的仿真时间。
time current_time;//定义一个时间类型的变量
initial
current_time = $time;//保存当前的仿真时间到变量current_time中。
(3)Verilog程序的基本结构
- verilog 包括大约100个关键字。
- 使用一个或者多个模块对数字电路进行建模。
模块module
- 模块名是模块唯一标识符。
- 端口类型说明必须明确。输入端口input、输出端口output、双向端口inout
- 参数定义将常量用符号常量代替。
- 数据类型定义,指定模块内使用的数据对象的类型。寄存器类型或者线网类型。
module 模块名(端口名1,端口名2,端口名3,...)
端口类型说明(input,output,inout)
参数定义(可选)
数据类型定义(wire,reg等)
实例化低层模块和基本门级元件;
连续赋值语句(assign);
过程块结构(initial和always)
行为描述语句;
endmodule
- 三种不同风格描述电路的功能。
(1)(结构描述方式)使用实例化低层模块的方法,调用其他已经写好的低层模块。或者直接调用verilog内部基本门级元件描述的电路电路接口。
(2)(数据流描述方式)使用连续赋值语句。适合组合逻辑电路建模。
(3)(行为描述方式)使用过程块语句结构(initial和always),使用比较抽象的高级程序语句。行为描述是学习的重点。
(4)附加一种描述方式(开关级描述方式),专门针对MOS管构成的逻辑电路进行建模。
示例
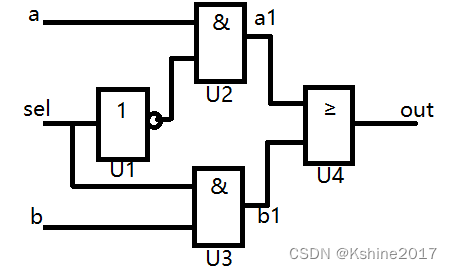
//简单电路的门级描述
module mux2tol(a,b,sel,out)
input a,b,sel;//定义输入信号
output out;//定义输出信号
wrie selnot,a1,b1;//定义内部节点信号数据类型
//下面对电路的逻辑功能进行描述
not U1(selnot,sel);
and U2(a1,a,selnot);
and U3(b1,b,sel);
or U4(out,a1,b1); //得到out输出信号
endmodule
(4)逻辑功能的仿真与测试
- 使用Quartus II软件。
- 仿真,建立一个矢量波形文件(.vwf)作为激励信号。
- 略,未完待续。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!