机器学习中的偏差和方差
评估机器学习模型的方法有很多种。我们可以使用MSE(均方误差)进行回归;精确度,召回率和ROC(特征接收器)用于分类问题。以类似的方式,偏差和方差帮助我们进行参数调整,并在几个构建的模型中确定更好的拟合模型。
偏差是由于对数据的错误假设而发生的一种错误,例如假设数据是线性的,而实际上数据遵循复杂的函数。另一方面,方差对训练数据的变化具有高度敏感性。这也是一种类型的错误,因为我们希望使我们的模型对噪声具有鲁棒性。机器学习中有两种错误。可约误差和不可约误差。偏差和方差属于可减少的误差。
什么是偏差
偏差被称为机器学习模型的预测值与正确值之间的差异。偏差高会在训练和测试数据中产生很大的误差。它建议算法应该总是低偏差的,以避免欠拟合的问题。偏差是由于机器学习过程中的错误假设而发生的系统性错误。
当假设在本质上过于简单或线性时,就会发生这种情况。请参阅下面的图表,以了解这种情况的示例。
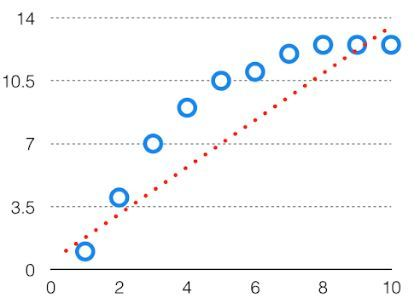
在这样一个问题中,假设看起来如下
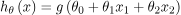
减少机器学习中高偏差的方法:
- 使用更复杂的模型:高偏差的主要原因之一是非常简化的模型。它将无法捕捉数据的复杂性。在这种情况下,我们可以通过增加深度神经网络的隐藏层数量来使我们的模式更加复杂。或者我们可以使用更复杂的模型,如多项式回归用于非线性数据集,CNN用于图像处理,RNN用于序列学习。
- 增加特征的数量:通过添加更多的特征来训练数据集将增加模型的复杂性。并提高其捕获数据中的底层模式的能力。
- 减少模型的正则化:L1或L2正则化等正则化技术可以帮助防止过拟合并提高模型的泛化能力。如果模型具有高偏差,则降低正则化的强度或将其完全移除可以帮助提高其性能。
- 增加训练数据的大小:增加训练数据的大小可以通过为模型提供更多从数据集学习的示例来帮助减少偏差。
什么是方差
模型对给定数据点的预测的变异性告诉我们数据的分布,称为模型的方差。具有高方差的模型对训练数据具有非常复杂的拟合,因此无法准确地拟合以前没有见过的数据。因此,这些模型在训练数据上表现得非常好,但在测试数据上具有很高的错误率。当一个模型的方差很高时,它被称为数据过拟合。过拟合是通过复杂的曲线和高阶假设准确地拟合训练集,但不是解决方案,因为未知数据的误差很高。在训练数据模型时,应将方差保持在较低水平。高方差数据如下所示。
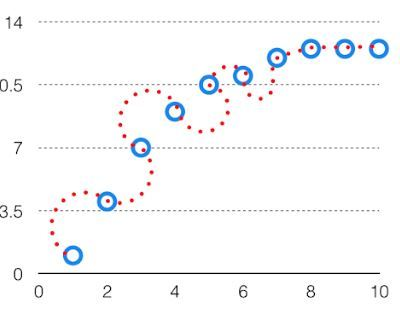
在这样一个问题中,假设看起来如下
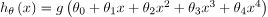
减少机器学习中方差的方法:
- 交叉验证:通过将数据多次拆分为训练集和测试集,交叉验证可以帮助识别模型是否过拟合或欠拟合,并可用于调整超参数以减少方差。
- 特征选择:通过选择唯一相关的特征将降低模型的复杂性。并且可以减小方差误差。
- 正则化:我们可以使用L1或L2正则化来减少机器学习模型中的方差。
- 嵌入方法:它将联合多个模型,以提高泛化性能。Bagging、boosting和stacking是常见的集成方法,可以帮助减少方差并提高泛化性能。
- 简化模型:降低模型的复杂性,例如减少神经网络中的参数或层数,也可以帮助减少方差并提高泛化性能。
- 提前停止:提前停止是一种用于防止过度拟合的技术,当验证集的性能停止改善时,停止深度学习模型的训练。
偏差方差权衡
如果算法太简单(假设线性方程),则它可能处于高偏差和低方差条件下,因此容易出错。如果算法拟合太复杂(假设具有高次方程),则它可能具有高方差和低偏差。在后一种情况下,新条目的性能不会很好。在这两种情况之间存在着某种东西,称为权衡或偏差方差权衡。这种复杂性的权衡就是偏差和方差之间存在权衡的原因。一个算法不可能同时变得更复杂和更简单。对于图来说,完美的权衡是这样的。
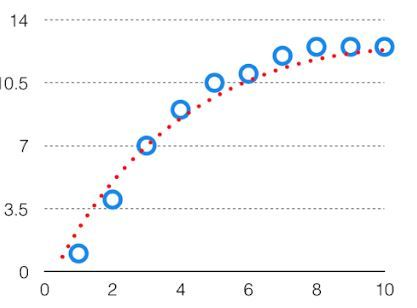
我们尝试使用偏差-方差权衡来优化模型的总误差值。
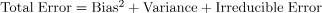
最佳拟合将由折衷点上的假设给出。显示权衡的复杂度图的误差给出为

这被称为为算法的训练选择的最佳点,其在训练和测试数据中给出低误差。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!