【全网首发】洛谷贪心题解合集2
1.P1413 坚果保龄球
链接——题目在这里！！！
题目描述
PVZ 这款游戏中，有一种坚果保龄球。zombie 从地图右侧不断出现，向左走，玩家需要从左侧滚动坚果来碾死他们。
我们可以认为地图是一个行数为?6，列数为?60的棋盘。zombie 出现的那一秒站在这一行的第?60?列，之后每秒向左移动一步。玩家可以随时在屏幕最某一行第一列摆放坚果，这一行的 zombie 瞬间全被滚过去的坚果碾死。如果 zombie 走到第?1?列没有被消灭，如果再向左走，则你的大脑就会被 zombie 吃掉。
现在有?n?只 zombie！告诉你每只 zombie 出现的时间以及在出现的行数（可能会同时出现同一位置的僵尸），请问至少需要多少坚果才能消灭所有的 zombie。
输入格式
第一行一个正整数n，表示 zombie 数量。
之后n行中，每行两个正整数P?和?t，分别表示 zombie 所在行和 zombie 出现的时间。
输出格式
一个正整数，最少需要的坚果数。
输入输出样例
输入 #1
10
1 1
1 61
2 1
2 60
3 1
3 2
3 3
3 4
4 1
4 99999
输出 #1
6
说明/提示
对于全部数据n≤2000，t≤100000，1≤P≤6。
解题思路
一道很简单的贪心模拟题~
想必大家已经想出贪心思路了：只有当一个zombie抵达第一列，我们才会不得不放坚果。很显然，这肯定是最佳方案。
具体实现思路是对每一行单独处理，对于每一只抵达第一行的zombie，用坚果杀死它，顺便杀死所有当前也在这行的zombie。
AC
#include<bits/stdc++.h>
using namespace std;
vector<int> a[7];
const int inf=1e6;
int n;
int main(){
cin >> n;
for (int i=1;i<=n;i++){
int x,y; cin >> x >> y;
a[x].push_back(y);
}
int ans=0;
for (int i=1;i<=6;i++){
sort(a[i].begin(),a[i].end());
int last=-inf;
for (int j=0;j<a[i].size();j++){
int x=a[i][j];
if (x>=last+60){
ans++;
last=x;
}
}
}
cout << ans << endl;
return 0;
}P1094 [NOIP2007 普及组] 纪念品分组
链接——题目在这里！！！
题目描述
元旦快到了，校学生会让乐乐负责新年晚会的纪念品发放工作。为使得参加晚会的同学所获得 的纪念品价值相对均衡，他要把购来的纪念品根据价格进行分组，但每组最多只能包括两件纪念品， 并且每组纪念品的价格之和不能超过一个给定的整数。为了保证在尽量短的时间内发完所有纪念品，乐乐希望分组的数目最少。
你的任务是写一个程序，找出所有分组方案中分组数最少的一种，输出最少的分组数目。
输入格式
共?n+2?行：
第一行包括一个整数?w，为每组纪念品价格之和的上限。
第二行为一个整数?n，表示购来的纪念品的总件数?G。
第?3～n+2?行每行包含一个正整数Pi??表示所对应纪念品的价格。
输出格式
一个整数，即最少的分组数目。
输入输出样例
输入 #1
100
9
90
20
20
30
50
60
70
80
90
输出 #1
6
说明/提示
50%?的数据满足：1≤n≤15。
100%的数据满足：1≤n≤3×104，80≤w≤200，5≤Pi?≤w。
解题思路
读入之后先用sort排序，然后用两个指针一起向中间走，每次选择都尽可能的让当前状态下最大的和最小的分在一组，如果不行就最大的单独分一组，这样贪心下来就是最少分的组了。证明如下：
如果最大的a[r]不与最小的a[l]分在一组，而是a[r]与a[i]在一组,a[l]与a[j]在一组，因为a[l]<=a[i]&&a[r]>=a[j],所以交换两者分组不影响后续选择，而a[r]如果不能与a[l]在一组，因为a[l]为当前最小值，所以a[r]只能单独为一组，所以贪心是 正确的。
AC
#include<bits/stdc++.h>
using namespace std;
const int maxn=3e4+3;
int n,a[maxn],w,ans;
int main(){
cin >> w >> n;
for (int i=1;i<=n;i++) cin >> a[i];
sort(a+1,a+n+1); ans=n;
int r=n;
for (int i=1;i<r;i++){
while (r>i&&a[i]+a[r]>w) r--;
if (r>i&&a[i]+a[r]<=w)
ans--,r--;
}
cout << ans << endl;
return 0;
}
//用sort很easy!!!^_^P1090 [NOIP2004 提高组] 合并果子
链接——题目在这里！！！
题目描述
在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过?n?1?次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为?1?，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。
例如有?3?种果子，数目依次为?11，2?,9?。可以先将?1?、2?堆合并，新堆数目为?3，耗费体力为?3?。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为?12?，耗费体力为?12?。所以多多总共耗费体力?=3+12=15。可以证明?15?为最小的体力耗费值。
输入格式
共两行。
第一行是一个整数?n(1≤n≤10000)?，表示果子的种类数。
第二行包含?n?个整数，用空格分隔，第i?个整数ai?(1≤ai?≤20000)?是第?i?种果子的数目。
输出格式
一个整数，也就是最小的体力耗费值。输入数据保证这个值小于231?。
输入输出样例
输入 #1
3
1 2 9?
输出 #1
15
说明/提示
对于?30%的数据，保证有 n≤1000：
对于?50%的数据，保证有?n≤5000；
对于全部的数据，保证有?n≤10000。
解题思路
这道题只需要把最小的两个果堆加起来就可以了，好多大佬都用的是优先队列，但由于本人太菜，只好用数组做。
如果这样想，那么每合并一次都需要排一次序，但事实上并不需要这么做（而且这样会超时，我之前用sort函数排就过了四个点，后面全都tle了），只需要给新合并的果堆找到所在的位置，并且将空的果堆删除就可以了。
AC
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+3;
int n,k,a[maxn];
int main(){
scanf("%d",&n);
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+n+1); reverse(a+1,a+n+1);
int ans=0;
while (n>1){
ans+=a[n-1]+a[n];
a[n-1]=a[n-1]+a[n]; n--;
int p=n;
while (p>1&&a[p]>a[p-1])
swap(a[p],a[p-1]),p--;
}
printf("%d\n",ans);
return 0;
}
P4447 [AHOI2018初中组] 分组
链接——www.luogu.com.cn/problem/P4447
小可可的学校信息组总共有?n?个队员，每个人都有一个实力值?ai?。现在，一年一度的编程大赛就要到了，小可可的学校获得了若干个参赛名额，教练决定把学校信息组的?n?个队员分成若干个小组去参加这场比赛。
但是每个队员都不会愿意与实力跟自己过于悬殊的队员组队，于是要求分成的每个小组的队员实力值连续，同时，一个队不需要两个实力相同的选手。举个例子：[1,2,3,4,5]?是合法的分组方案，因为实力值连续；[1,2,3,5]?不是合法的分组方案，因为实力值不连续[0,1,1,2]?同样不是合法的分组方案，因为出现了两个实力值为?1?的选手。
如果有小组内人数太少，就会因为时间不够而无法获得高分，于是小可可想让你给出一个合法的分组方案，满足所有人都恰好分到一个小组，使得人数最少的组人数最多，输出人数最少的组人数的最大值。
注意：实力值可能是负数，分组的数量没有限制。
输入格式
输入有两行：
第一行一个正整数?n，表示队员数量。
第二行有?n?个整数，第?i?个整数?ai??表示第?i?个队员的实力。
输出格式
输出一行，包括一个正整数，表示人数最少的组的人数最大值。
输入输出样例
输入 #1
7
4 5 2 3 -4 -3 -5
输出 #1
3
说明/提示
【样例解释】 分为?22?组，一组的队员实力值是{4,5,2,3}，一组是?{?4,?3,?5}，其中最小的组人数为?3，可以发现没有比?3?更优的分法了。
【数据范围】
对于?100%的数据满足：1≤n≤100000，ai?≤109。
本题共?10?个测试点，编号为1～10，每个测试点额外保证如下：
| 测试点编号 | 数据限制 |
|---|---|
| 1~2 | n≤6,1≤ai?≤100 |
| 3～4 | n≤1000,1≤ai?≤105?且?ai??互不相同 |
| 5～6 | n≤100000,ai??互不相同 |
| 7～8 | n≤100000,1≤ai?≤105 |
| 9～10 | n≤100000,?109≤ai?≤109 |
解题思路
也许是一种奇妙的思路？
我们用类似条形统计图的方式，在数轴上统计各个实力值出现的次数。以样例为例：
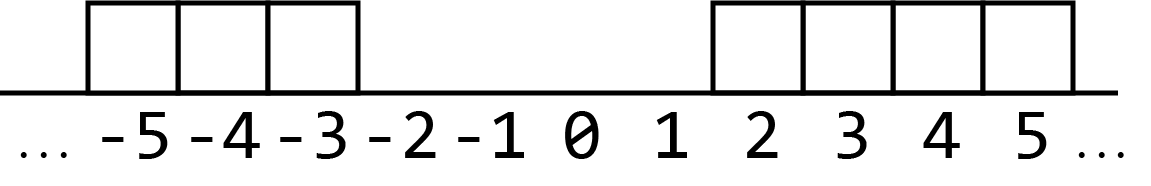
题目中的“分组”，就可以理解为在方格中画线——被同一条线相连的方格所对应的同学被分为一组。如：
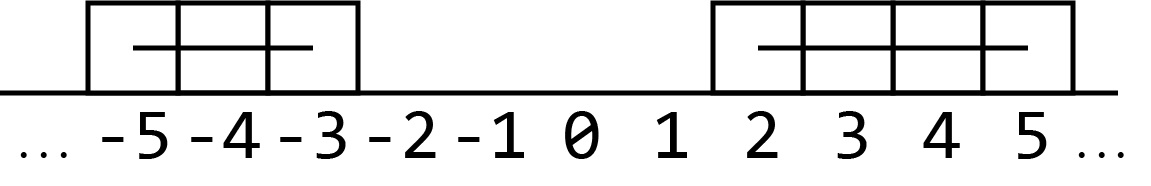
再演示一个稍微复杂一点的图（删去了数轴）：
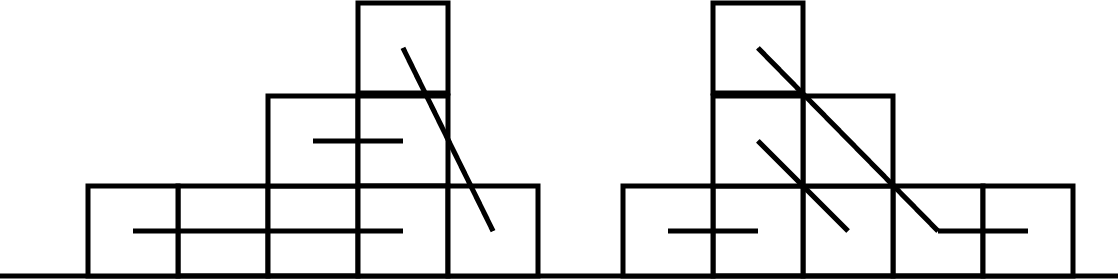
也许这样不是特别直观？我们规定，删除被画过线的方格，且总是在最下方一行画线：
为方便表述，定义一条线所连接的方格数为这条线的长度，某一列当前的方块数为这一列的高度。
至此，“分组”问题被转化成了一个“俄罗斯方块”式的问题。接下来，我们要研究如何使人数最少的组别人数最大——也就是如何使长度最短的线长度最大。
不妨令每一次画线都从最左边一列开始。
每次都画到底，可以吗？
显然，大多数情况下这不是最优解。最后可能会剩下一个方块“一枝独秀”：
出现这种情况的根本原因是什么？我们发现，“一枝独秀”的方块总是出现在高度较高的几列。
如何解决？我们需要改变画线的方式：
如果右边一列的高度不低于当前列，则连接右边一列最下方的方块。反之，停止画线。
这样，最靠左的一个“峰”相较其右边一列的高度差就不断减小，直到相同。如此反复。记录所画所有线的最短长度，即为答案。
AC
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+3;
int a[maxn],n,ans;
int p[maxn],q[maxn],s,t;
int main(){
cin >> n;
for (int i=1;i<=n;i++) cin >> a[i];
sort(a+1,a+n+1); ans=n+1;
s=1; p[1]=1;
for (int i=2;i<=n;i++){
if (a[i]>a[i-1]+1){
for (int j=1;j<=s;j++) ans=min(ans,p[s]); s=0;
for (int j=1;j<=t;j++) ans=min(ans,q[t]); t=0;
s=1; p[1]=1;
} else {
if (a[i]>a[i-1]){
for (int j=1;j<=t;j++) ans=min(ans,q[t]); t=s;
for (int j=1;j<=s;j++) q[j]=p[j]; s=0;
sort(q+1,q+t+1); reverse(q+1,q+t+1);
}
if (t>0){
s++; p[s]=q[t]+1; t--;
} else {
s++; p[s]=1;
}
}
}
for (int i=1;i<=s;i++) ans=min(ans,p[s]);
for (int i=1;i<=t;i++) ans=min(ans,q[t]);
cout << ans << endl;
return 0;
}?结尾
希望大家多多关注。
本篇文章共5434字，如果你能支持一下我，我十分感谢！！！
如果有人想在洛谷上做题，可以点下方链接：
如果你喜欢或想了解一下其他的算法，可以看看以下这些：
题目详解系列（部分）：
游戏系列：
C++讲解系列（算法）：
C++:第十二讲DFS深搜（二）_c++匿名函数dfs-CSDN博客
前缀和与差分：
贪心：
C++讲解系列（基础入门）：
排序：
函数：
C++第6讲max和min函数_c++ min函数-CSDN博客
for循环&数组：
if语句&else语句及运算：
C++第三讲：C++中的逻辑运算符及if else语句-CSDN博客
基础：
欢迎收看，希望大家能三连！
最后认识一下，我是爱编程的喷火龙廖，我们有缘再见！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！