应用光学研读——第二章 球面和共轴球面系统
第二章 球面和共轴球面系统
2.1 光线经过单个折射球面的折射
共轴球面系统:绝大部分光学系统由球面和平面(折射面和反射面)组成,各球面球心在一条直线上,形成系统的对称轴,即光轴,这样的系统称为共轴球面系统。
为进行光线的光路计算,可以先对单个折射球面进行讨论,推导近轴光计算公式和讨论光学系统近轴光的特性.
1. 符号规则
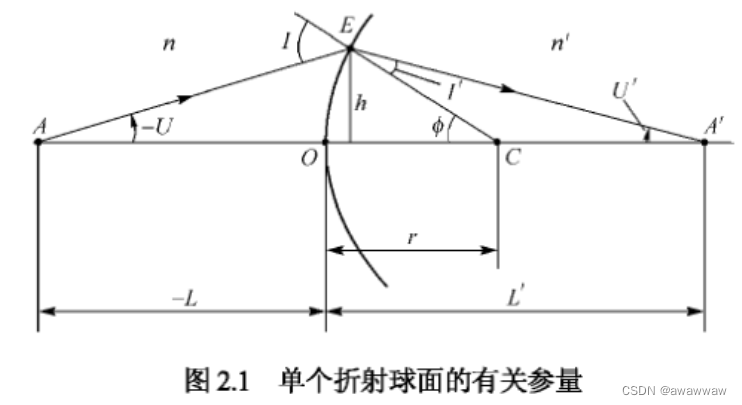
| 含义 | |
|---|---|
| OE | 折射面,折射率为n和n’的两个介质的分界面 |
| C | 球心 |
| OC | 球面曲率半径,数值为r |
| O | 顶点:光轴与球面的交点 |
参量符号的限定如下:
| 参量 | 符号限定 |
|---|---|
| 沿轴线段 | O为原点,O到线段另一点的方向与光线方向相同,则为正,反之,则为负 |
| 垂轴线段 | 光轴以上为正,光轴以下为负 |
| 光轴与光线夹角 | 光轴与光线的锐角来度量,光轴转向光线顺时针为正,逆时针为负 |
| 光轴与法线夹角 | 光线以锐角方向转向法线,顺时针为正,逆时针为负 |
参量符号限定的意义:
为了使确定光线位置的参量更有确切的含意,使以后推导出的光线的光路计算公式不论是凸折射面或凹折射面、光线与光轴交点的位置在顶点的左边还是右边、光线在光轴以上还是以下均能普遍适用,必须对这些参量及其他有关量的符号加以规定。
2. 实际光线经过单个折射球面的光路计算公式
应用两个三角形的正弦定律、折射定律等可得像方截距:
L ′ = r + r s i n I ′ s i n U ′ (2.4) L' = r + r\frac{sinI'}{sinU'}\tag{2.4} L′=r+rsinU′sinI′?(2.4)
L为定值时,L’是U的函数,如下图所示:
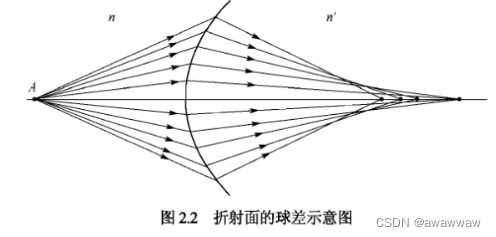
球差:像方光束不再和光轴交于一点,失去了同心性。故轴上一点以有限孔径角的光束经过单个折射面成像时,一般是不完善的,这种现象称为球面像差,简称,球差。
3. 近轴光的光路计算公式
若A发出的入射于球面的光线与光轴夹角非常小,其相应的角度I,I’,U’也非常小,这些角度的正弦值可以用弧度代替,以对应小写字母表示,对上述进行运算得到公式如下:
n
[
1
r
?
1
l
]
=
n
′
[
1
r
?
1
l
′
]
=
Q
(2.7)
n[\frac{1}{r} - \frac{1}{l}] = n'[\frac{1}{r} - \frac{1}{l'}] = Q\tag{2.7}
n[r1??l1?]=n′[r1??l′1?]=Q(2.7)
n
′
u
′
?
n
u
=
n
′
?
n
r
h
(2.8)
n'u'-nu = \frac{n'-n}{r}h\tag{2.8}
n′u′?nu=rn′?n?h(2.8)
n
′
l
′
?
n
l
=
n
′
?
n
r
(2.9)
\frac{n'}{l'} - \frac{n}{l} = \frac{n'-n}{r}\tag{2.9}
l′n′??ln?=rn′?n?(2.9)
Q为阿贝不变量,对于一个折射球面,物空间和像空间的Q值相同,数值随共轭点的位置不同而不同。三个式子互相等价。式2.8描述折射前后夹角的关系,式2.9描述l和l’的关系。
2.2 单个折射面的成像倍率、拉赫不变量
1. 垂轴倍率
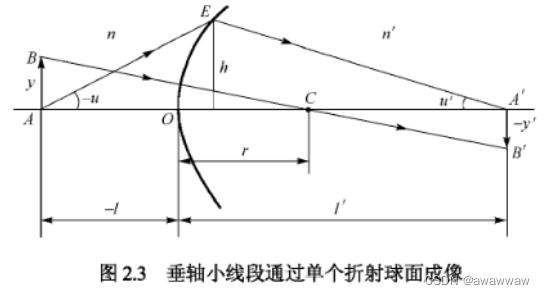
如图所示,垂轴小线段通过折射球面成像A’B’,AB像高y,A’B’像高y’,像的大小与物的大小的比值称为垂轴倍率,用b表示:
b = y ′ y (2.10) b = \frac{y'}{y}\tag{2.10} b=yy′?(2.10)
经过计算,得到
b = n l ′ n ′ l (2.11) b = \frac{nl'}{n'l}\tag{2.11} b=n′lnl′?(2.11)
2. 轴向倍率
轴向倍率是广州光轴上一对共轭点沿轴移动量之间的关系。用希腊字母α表示,定义为:
α
=
d
l
′
/
d
l
(2.12)
α = dl'/dl\tag{2.12}
α=dl′/dl(2.12)
对式2.9微分,运算得到:
α = n ′ n b 2 (2.14) α = \frac{n'}{n}b^2\tag{2.14} α=nn′?b2(2.14)
如果物体时一个正方体,则因垂轴倍率和轴向倍率的不一致,其像不再是正方体。
折射球面轴向倍率为正值,表示物点沿轴移动,像点向同样的方向沿轴移动。
式2.14适用于dl很小时,如果物点沿轴移动有限距离,则可以计算首尾距离得到:
a = l 2 ′ ? l 1 ′ l 2 ? l 1 (2.15) a = \frac{l_2'-l_1'}{l_2-l_1}\tag{2.15} a=l2??l1?l2′??l1′??(2.15)
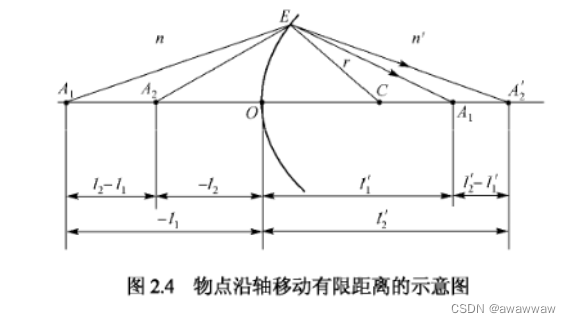
计算得到:
a = n ′ n b 1 b 2 (2.16) a = \frac{n'}{n}b_1b_2\tag{2.16} a=nn′?b1?b2?(2.16)
3. 角倍率
g = u ′ / u (2.17a) g = u'/u\tag{2.17a} g=u′/u(2.17a)
g = n n ′ 1 b (2.17b) g = \frac{n}{n'}\frac{1}{b}\tag{2.17b} g=n′n?b1?(2.17b)
4. 三个倍率之间的关系
α g = b (2.19) αg = b \tag{2.19} αg=b(2.19)
5. 拉格朗日-赫姆霍兹不变量
拉赫公式:
n u y = n ′ u ′ y ′ = J (2.20) nuy = n'u'y' = J\tag{2.20} nuy=n′u′y′=J(2.20)
2.3 共轴球面系统
前面单个折射球面不能作为一个基本成像元件(反射镜是折射面的特例),基本成像元件是至少由两个球面或非球面所构成的透镜。
1. 共轴球面系统的转面公式
一个共轴球面系统由一系列数据所确定:
- 各个折射球面的曲率半径: r 1 , r 2 , . . . , r k r_1,r_2,...,r_k r1?,r2?,...,rk?;
- 各相邻折射面顶点之间的间隔: d 1 , d 2 , . . . , d k ? 1 d_1,d_2,...,d_{k-1} d1?,d2?,...,dk?1?;
- 各个球面间介质的折射率: n 1 , n 2 , . . . , n k + 1 n_1,n_2,...,n_{k+1} n1?,n2?,...,nk+1?。
n
2
=
n
1
′
,
n
3
=
n
2
′
,
.
.
.
,
n
k
=
n
k
?
1
′
n_2 = n_1', n_3 = n_2',... , n_k = n_{k-1}'
n2?=n1′?,n3?=n2′?,...,nk?=nk?1′?
u
2
=
u
1
′
,
u
3
=
u
2
′
,
.
.
.
,
u
k
=
u
k
?
1
′
(2.21)
u_2 = u_1', u_3 = u_2',... , u_k = u_{k-1}' \tag{2.21}
u2?=u1′?,u3?=u2′?,...,uk?=uk?1′?(2.21)
y
2
=
y
1
′
,
y
3
=
y
2
′
,
.
.
.
,
y
k
=
y
k
?
1
′
y_2 = y_1', y_3 = y_2',... , y_k = y_{k-1}'
y2?=y1′?,y3?=y2′?,...,yk?=yk?1′?
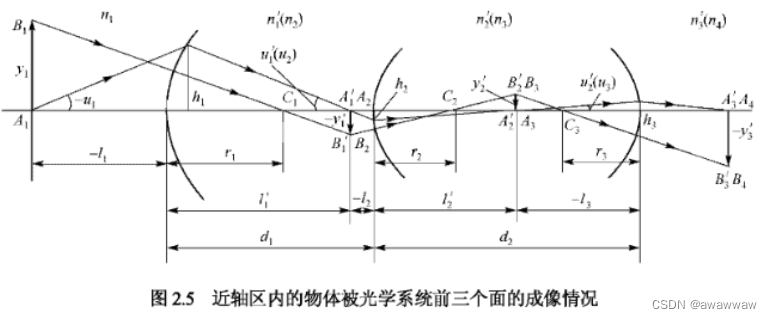
l 2 = l 1 ′ ? d 1 , l 3 = l 2 ′ ? d 2 , . . . , l k = l k ? 1 ? d k ? 1 (2.22) l_2 = l_1' - d_1,l_3 = l_2' - d_2,... , l_k = l_{k-1} - d_{k-1}\tag{2.22} l2?=l1′??d1?,l3?=l2′??d2?,...,lk?=lk?1??dk?1?(2.22)
2. 共轴球面系统的拉赫不变量
n 1 u 1 y 1 = n 2 u 2 y 2 = . . . = n k u k y k = n k ′ u k ′ y k ′ = J (2.25) n_1u_1y_1 = n_2u_2y_2=...=n_ku_ky_k=n_k'u_k'y_k' = J\tag{2.25} n1?u1?y1?=n2?u2?y2?=...=nk?uk?yk?=nk′?uk′?yk′?=J(2.25)
3. 共轭球面系统的倍率计算
垂轴倍率
b = b 1 b 2 b 3 . . . . b k (2.27) b = b_1b_2b_3....b_k \tag{2.27} b=b1?b2?b3?....bk?(2.27)
b = n 1 n k ′ u 1 u k ′ (2.28) b = \frac{n_1}{n_k'}\frac{u_1}{u_k'}\tag{2.28} b=nk′?n1??uk′?u1??(2.28)
轴向倍率
a = a 1 a 2 a 3 . . . . a k (2.29) a = a_1a_2a_3....a_k\tag{2.29} a=a1?a2?a3?....ak?(2.29)
a = n k ′ n 1 b 2 (2.30) a = \frac{n_k'}{n_1}b^2\tag{2.30} a=n1?nk′??b2(2.30)
角倍率
g = g 1 g 2 . . . . g k (2.31) g = g_1g_2....g_k\tag{2.31} g=g1?g2?....gk?(2.31)
g = n 1 n k ′ 1 b (2.32) g = \frac{n_1}{n_k'}\frac{1}{b}\tag{2.32} g=nk′?n1??b1?(2.32)
综合:
a g = b (2.33) ag = b\tag{2.33} ag=b(2.33)
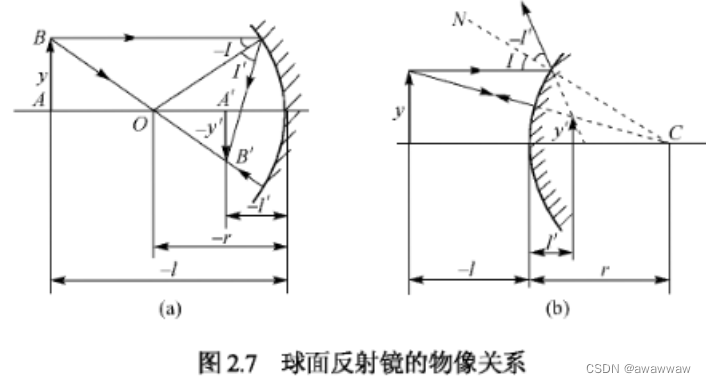
2.4 球面反射镜
球面反射镜的物象公式
n ′ = ? n n' = -n n′=?n
1 l ′ + 1 l = 2 r (2.34) \frac{1}{l'} + \frac{1}{l} = \frac{2}{r}\tag{2.34} l′1?+l1?=r2?(2.34)
球面反射镜的成像倍率
b = ? l ′ l , a = ? b 2 , g = ? 1 b (2.35) b = -\frac{l'}{l},a = -b^2,g = -\frac{1}{b}\tag{2.35} b=?ll′?,a=?b2,g=?b1?(2.35)
球面反射镜的拉赫不变量
J = u y = ? u ′ y ′ J = uy = -u'y' J=uy=?u′y′
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 常用rtmp、m3u8、flv、mp4直播流在线测试地址
- Elasticsearch可视化平台Kibana [ES系列] - 第498篇
- 算法训练营Day32
- web学习笔记(十)
- 羊大师提示人生下半场,健康是关键
- 【CF闯关练习】—— 1400分(C. Make Good、B. Applejack and Storages)
- DNS 正/反向解析 主从复制 分离解析
- Java电子招投标采购系统源码-适合于招标代理、政府采购、企业采购、等业务的企业
- 游戏美术的技与艺
- #2Vite+Vue3+SpringMVC前后端分离 解决跨域问题和session每次请求不一致问题