算法(4)——前缀和

class Solution {
public:
    int pivotIndex(vector<int>& nums) 
    {
        int n=nums.size();
        vector<int> f(n),g(n);
        //前缀和
        for(int i=1;i<n;i++)
            f[i]=nums[i-1]+f[i-1];
        //后缀和
        for(int i=n-2;i>=0;i--)
            g[i]=nums[i+1]+g[i+1];

        for(int i=0;i<n;i++)
        {
            if(g[i]==f[i])
                return i;
        }
        return -1;
    }
};

3.3、除自身以外数组的乘积

238. 除自身以外数组的乘积 - 力扣（LeetCode）

题目描述：

算法思路：

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) 
    {
        int n=nums.size();
        vector<int> g(n),f(n);
        //前缀积
        f[0]=g[n-1]=1;
        for(int i=1;i<n;i++)
            f[i]=f[i-1]*nums[i-1];
        //后缀积
        for(int i=n-2;i>=0;i--)
            g[i]=g[i+1]*nums[i+1];

        vector<int> arr(n);
        for(int i=0;i<n;i++)
        {
            arr[i]=g[i]*f[i];
        }
        return arr;
    }
};

560. 和为 K 的子数组 - 力扣（LeetCode）

题目描述：

算法思路：

代码实现：

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) 
    {
        unordered_map<int,int> hash;
        int sum=0,ret=0;
        hash[0]=1;
        for(auto x:nums)
        {
            sum+=x;
            if(hash.count(sum-k))
            {
                ret+=hash[sum-k];
            }
            hash[sum]++;
        }
        return ret;
    }
};

3.5、和可被K整除的子数组

974. 和可被 K 整除的子数组 - 力扣（LeetCode）

题目描述：

算法思路:

例如： (26 - 2) % 12 == 0 ，那么 26 % 12 == 2 % 12 == 2 。

? c++ 中负数取模的结果，以及如何修正「负数取模」的结果

a. c++ 中关于负数的取模运算，结果是「把负数当成正数，取模之后的结果加上?个负号」。

例如： -1 % 3 = -(1 % 3) = -1

b. 因为有负数，为了防?发?「出现负数」的结果，以 (a % n + n) % n 的形式输出保证为正。

例如： -1 % 3 = (-1 % 3 + 3) % 3 = 2

设 i 为数组中的任意位置，? sum[i] 表? [0, i] 区间内所有元素的和。

? 想知道有多少个「以 i 为结尾的可被 k 整除的?数组」，就要找到有多少个起始位置为 x1,x2, x3... 使得 [x, i] 区间内的所有元素的和可被 k 整除。

? 设 [0, x - 1] 区间内所有元素之和等于 a ， [0, i] 区间内所有元素的和等于 b ，可得 (b - a)%k ==0?

? 由同余定理可得， [0, x - 1] 区间与 [0, i] 区间内的前缀和同余。于是问题就变成：

? 找到在 [0, i - 1] 区间内，有多少前缀和的余数等于 sum[i] % k 的即可。

我们不?真的初始化?个前缀和数组，因为我们只关?在 i 位置之前，有多少个前缀和等于

sum[i] - k 。因此，我们仅需??个哈希表，?边求当前位置的前缀和，?边存下之前每?种前缀和出现的次数。

代码实现：

class Solution {
public:
    int subarraysDivByK(vector<int>& nums, int k) 
    {
        unordered_map<int,int> hash;  //第一个int存余数，第二个存个数
        int sum=0,ret=0;
        hash[0%k]=1; 
        for(auto x:nums)
        {
            sum+=x;
            int r=(sum%k+k)%k;
            if(hash.count(r)) ret+=hash[r];
            hash[r]++;
        }
        return ret;
    }
};

3.6、连续数组

525. 连续数组 - 力扣（LeetCode）

题目描述：

算法思路：

稍微转化?下题?，就会变成我们熟悉的题：

? 本题让我们找出?段连续的区间， 0 和 1 出现的次数相同。

? 如果将 0 记为 -1 ， 1 记为 1 ，问题就变成了找出?段区间，这段区间的和等于 0 。

? 于是，就和 和为 K 的?数组 这道题的思路?样

设 i 为数组中的任意位置，? sum[i] 表? [0, i] 区间内所有元素的和。

想知道最?的「以 i 为结尾的和为 0 的?数组」，就要找到从左往右第?个 x1 使得 [x1, i]

区间内的所有元素的和为 0 。那么 [0, x1 - 1] 区间内的和是不是就是 sum[i] 了。于是问题就变成：

? 找到在 [0, i - 1] 区间内，第?次出现 sum[i] 的位置即可。

我们不?真的初始化?个前缀和数组，因为我们只关?在 i 位置之前，第?个前缀和等于 sum[i]的位置。因此，我们仅需??个哈希表，?边求当前位置的前缀和，?边记录第?次出现该前缀和的位置。

代码实现：

class Solution {
public:
    int findMaxLength(vector<int>& nums) 
    {
        unordered_map<int,int> hash;
        hash[0]=-1;
        int sum=0,ret=0;
        for(int i=0;i<nums.size();i++)
        {
            sum+=nums[i]==0?-1:1;//当前位置的前缀和,将0变-1
            if(hash.count(sum)) ret=max(ret,i-hash[sum]);
            else hash[sum]=i;
        }
        return ret;
    }
};

四、二位前缀和

和一维前缀和的原理类似，只不过二维前缀和求的是一个矩阵中所有元素的和。

例如：对与 x = 4，y = 3?这么一组输入，就是将原矩阵序列中蓝色区域的元素相加，得到的结果便是前缀和矩阵S中?S[ 4 ][ 3 ] 的值。

例如上图：我们要求蓝色矩阵中所有元素的和。

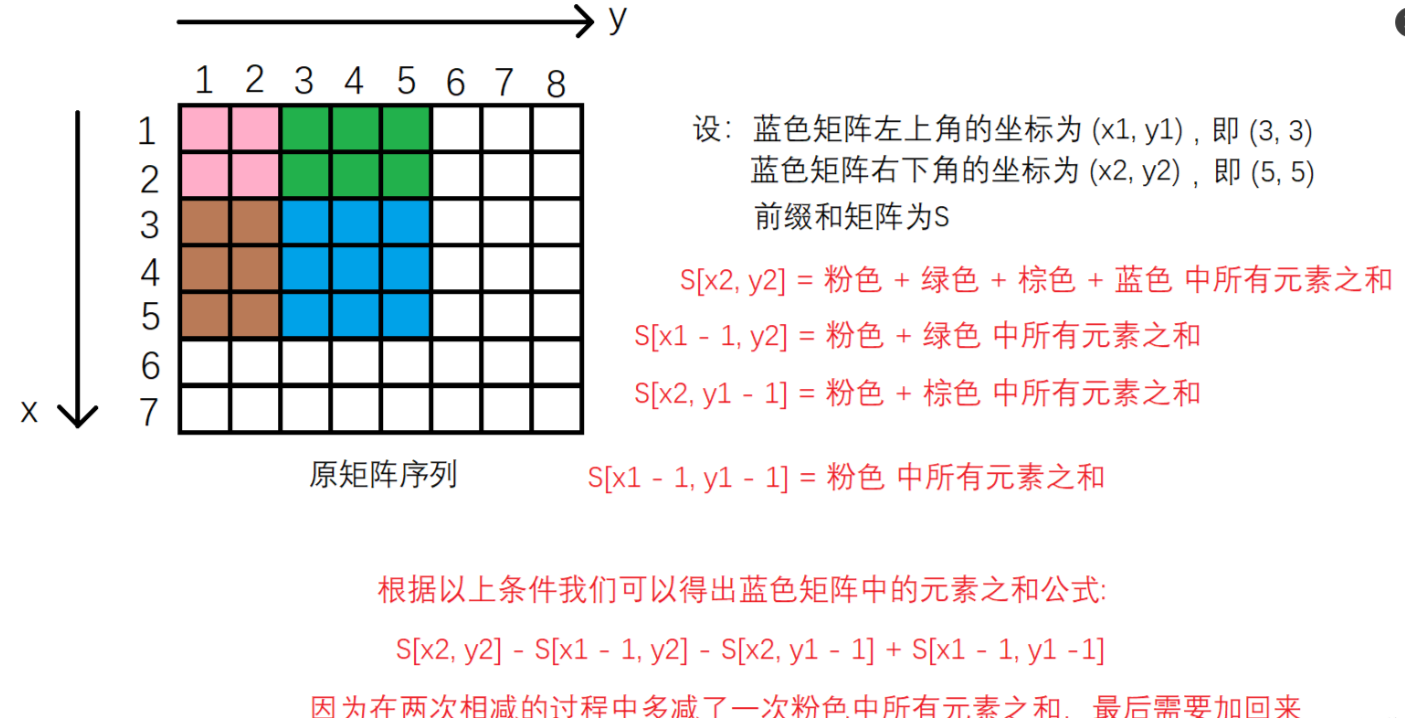
?现在就差最后一步了，怎么求出前缀和矩阵中的每一个值嘞？？同理利用递推关系求就阔以啦。

? S[ i ][ j ] = S[ i - 1 ][ j ] + S[ i ][ j - 1?] -?S[ i - 1][ j - 1 ] + a[ i ][ j ]

五、二维前缀和OJ题

4.1、二维前缀和

【模板】二维前缀和_牛客题霸_牛客网 (nowcoder.com)

题目描述：

算法思路：

• 首先对矩阵进行预处理，得到对应的前缀和矩阵。
• 利用前缀和矩阵相应区域的加减运算，即可得到对应子矩阵中所有元素的累加和。

图解展示（图中presum[3][4]除了包括绿色部分，还包括其它重叠的部分，其它几项也一样，另外presum[1][1]被多减了一次，所以最后要加一次）：

代码实现：

#include <iostream>
#include<vector>
using namespace std;

int main() 
{
    int n,m,q;
    cin>>n>>m>>q;
    vector<vector<long long>> arr(n+1,vector<long long>(m+1));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>arr[i][j];
        }
    }

    vector<vector<long long>> dp(n+1,vector<long long>(m+1));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];
        }
    }

    int x1,x2,y1,y2;
    while(q--)
    {
        cin>>x1>>y1>>x2>>y2;
        cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;
    }
    return 0;
}

4.2、矩阵区域和

1314. 矩阵区域和 - 力扣（LeetCode）

题目描述

算法思路：

代码实现：

class Solution {
public:
    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k)    
    {
        int m=mat.size(),n=mat[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1));

        //预处理矩阵
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
               dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
        //使用前缀和矩阵
        vector<vector<int>> ret(m,vector<int>(n));
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                int x1 = max(0, i - k) + 1, y1 = max(0, j - k) + 1;
                int x2 = min(m - 1, i + k) + 1, y2 = min(n - 1, j + k) + 1;
                ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
            }
        }
        return ret;
    }
};