AI绘画中VAE压缩图像
介绍
在Stable Diffusion中,所有的去噪和加噪过程并非在图像空间直接进行,而是通过VAE模块将图像编码到一个低维空间。
这个低维空间的“分辨率”低于原始图像空间,有利于快速地完成加噪和去噪过程。
最后再将编码空间中的噪声表示解码恢复为图像空间,完成去噪或加噪操作。
采用这种编码-解码的流程,可以避免在高维图像空间直接操作带来的计算资源消耗,也更容易控制和操作噪声信号。
VAE模块承担了编码图像到隐空间然后操作的功能,是Stable Diffusion实现高效噪声增减的关键。
概念
变分自编码器(Variational Autoencoder, VAE)中的潜在空间(latent space)是一个核心概念,对理解 VAE 的工作原理至关重要。
潜在空间指的是一个较低维度的表示空间,在该空间中,数据的高维特性被编码为更为简洁的形式。在 VAE 框架中,潜在空间充当着数据的内部、抽象表示,通常捕获了数据的基本特征和结构。

在这个示例中:
- “输入数据”是模型的输入,比如一张图像。
- “编码器”将输入数据映射到潜在空间的分布参数,通常是均值(μ)和方差(σ)。
- 在“潜在空间参数”步骤,从分布中“抽样”以产生潜在空间的样本点。
- “解码器”接收潜在空间中的样本点,并尝试重构与原始输入类似的数据。
- “重构数据”是模型的最终输出,是对输入数据的重构或生成版本。
潜在空间的重要性
- 特征提取:在潜在空间中,数据的关键特征被提取和压缩,去除了冗余信息。
- 数据生成:由于其连续性,潜在空间允许我们通过在其内进行抽样来生成新的数据实例,这些数据实例在某种程度上类似于原始数据集中的样本。
- 数据表示:潜在空间提供了一种更加有效的方式来表示复杂数据,为数据的进一步分析和处理提供了可能。
历史
变分自编码器(Variational Autoencoder, VAE)的历史和演变可以概述为以下几个关键阶段:
-
初始发展(2013年左右):
- VAE 的概念最初由 Kingma 和 Welling 在 2013 年的论文《Auto-Encoding Variational Bayes》中提出。https://arxiv.org/abs/1312.6114
- 这一阶段的创新在于引入了一种新的生成模型框架,结合了深度学习与贝叶斯推断方法。VAE 提供了一种有效的方式来学习和推断复杂数据的潜在表示。
-
理论和应用的发展(2014-2016年):
- 在这一时期,研究者开始深入探讨 VAE 的理论基础,包括其与传统自编码器的区别、潜在空间的属性以及优化技术。
- 应用上,VAE 被用于图像生成、语音处理和推荐系统等多个领域,其能力在处理复杂数据分布时展现出显著优势。
-
结构和算法的创新(2017-2019年):
- 随着深度学习技术的发展,VAE 的结构和算法得到了显著改进,如引入卷积神经网络(CNN)来处理图像数据,改善了模型的生成质量和效率。
- 也出现了一些变体,如条件 VAE(CVAE)和序列变分自编码器(SVAE),这些变体扩展了 VAE 在特定场景下的应用。
-
集成和多模态学习(2020年至今):
- VAE 开始与其他深度学习模型(如 GAN、Transformer)结合,形成更加复杂和强大的混合模型。
- 在多模态学习领域,VAE 被用来融合不同类型的数据,如图像和文本,从而在生成任务中实现更丰富的表达能力。
架构
https://arxiv.org/abs/1312.6114
VAE 的核心是通过一个编码器将数据映射到潜在空间,然后通过一个解码器重构数据。在潜在空间中,数据的表示是基于随机分布的,通常是高斯分布。这种表示允许模型在生成新数据时捕捉输入数据的关键特征。
关于 VAE 的数学公式表达,它们主要围绕以下几个方面构建:
-
编码器的输出(Encoder Output):
- 编码器将输入数据 ( x ) 映射到潜在空间中的一个分布,通常这个分布被假设为高斯分布,其参数是均值 ( μ ) ( \mu ) (μ) 和方差 ( σ 2 ) ( \sigma^2 ) (σ2)
- 数学上表达为 q ? ( z ∣ x ) = N ( z ; μ , σ 2 I ) q_\phi(z|x) = \mathcal{N}(z; \mu, \sigma^2 I) q??(z∣x)=N(z;μ,σ2I),其中 ( ? ) ( \phi ) (?) 是编码器的参数。
-
重构误差(Reconstruction Loss):
- 这部分是通过解码器从潜在空间重构输入数据 ( x ) ( x ) (x) 时产生的误差。
- 常用的度量方法是均方误差或交叉熵,具体取决于数据的性质。
-
KL 散度(Kullback-Leibler Divergence):
- KL 散度用于衡量编码器输出的分布 ( q ? ( z ∣ x ) ) ( q_\phi(z|x) ) (q??(z∣x)) 与先验分布 ( p ( z ) ) ( p(z) ) (p(z))(通常是标准高斯分布)之间的差异。
- 公式为 KL [ q ? ( z ∣ x ) ∣ ∣ p ( z ) ] \text{KL}[q_\phi(z|x) || p(z)] KL[q??(z∣x)∣∣p(z)],这项帮助正则化潜在空间,防止过拟合。
-
变分下界(Variational Lower Bound, ELBO):
- VAE 的目标是最大化每个输入 ( x ) ( x ) (x) 的证据下界(ELBO),其表达为: ELBO = E q ? ( z ∣ x ) [ log ? p θ ( x ∣ z ) ] ? KL [ q ? ( z ∣ x ) ∣ ∣ p ( z ) ] \text{ELBO} = \mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)] - \text{KL}[q_\phi(z|x) || p(z)] ELBO=Eq??(z∣x)?[logpθ?(x∣z)]?KL[q??(z∣x)∣∣p(z)]
- 这里 E q ? ( z ∣ x ) [ log ? p θ ( x ∣ z ) ] \mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)] Eq??(z∣x)?[logpθ?(x∣z)] 是重构误差的期望, KL [ q ? ( z ∣ x ) ∣ ∣ p ( z ) ] \text{KL}[q_\phi(z|x) || p(z)] KL[q??(z∣x)∣∣p(z)] 是正则化项。
这些公式和原理共同构成了 VAE 的数学框架,使其成为一种强大的生成模型。在训练过程中,VAE 通过调整编码器和解码器的参数 ( ? ) ( \phi ) (?) 和 ( θ ) ( \theta ) (θ) 来最大化 ELBO,从而学习到有效的数据表示。
-
优化目标:ELBO 是 VAE 训练过程中的优化目标,模型通过最大化 ELBO 来训练。
-
平衡重构与正则化:ELBO 结合了两个重要部分——重构误差(数据的重构质量)和 KL 散度(潜在空间的正则化)。这种结合使模型在学习有效的数据表示的同时,避免了过拟合。
-
提升数据生成质量:通过最大化 ELBO,VAE 能够更好地学习潜在空间中数据的分布,从而提高生成新数据样本的质量。

import torch
import torch.nn as nn
import torch.nn.functional as F
class Encoder(nn.Module):
# 编码器定义
def __init__(self, input_dim, hidden_dim, latent_dim):
super(Encoder, self).__init__()
self.linear1 = nn.Linear(input_dim, hidden_dim)
self.mean = nn.Linear(hidden_dim, latent_dim)
self.logvar = nn.Linear(hidden_dim, latent_dim)
def forward(self, x):
# 前向传播过程
hidden = F.relu(self.linear1(x))
mean = self.mean(hidden)
logvar = self.logvar(hidden)
return mean, logvar
class Decoder(nn.Module):
# 解码器定义
def __init__(self, latent_dim, hidden_dim, output_dim):
super(Decoder, self).__init__()
self.linear1 = nn.Linear(latent_dim, hidden_dim)
self.linear2 = nn.Linear(hidden_dim, output_dim)
def forward(self, z):
# 前向传播过程
hidden = F.relu(self.linear1(z))
recon_x = torch.sigmoid(self.linear2(hidden))
return recon_x
class VAE(nn.Module):
# VAE模型定义
def __init__(self, input_dim, hidden_dim, latent_dim):
super(VAE, self).__init__()
self.encoder = Encoder(input_dim, hidden_dim, latent_dim)
self.decoder = Decoder(latent_dim, hidden_dim, input_dim)
def reparameterize(self, mean, logvar):
# 重参数化技巧
std = torch.exp(0.5*logvar)
eps = torch.randn_like(std)
return mean + eps*std
def forward(self, x):
# 定义模型的前向传播
mean, logvar = self.encoder(x)
z = self.reparameterize(mean, logvar)
recon_x = self.decoder(z)
return recon_x, mean, logvar
def loss_function(self, recon_x, x, mean, logvar):
# 定义损失函数
BCE = F.binary_cross_entropy(recon_x, x, reduction='sum')
KLD = -0.5 * torch.sum(1 + logvar - mean.pow(2) - logvar.exp())
return BCE + KLD
# 参数设定
input_dim = 784 # 例如MNIST数据的维度
hidden_dim = 400
latent_dim = 20
# 初始化模型、优化器等
model = VAE(input_dim, hidden_dim, latent_dim)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
# 训练过程
for epoch in range(num_epochs):
model.train()
train_loss = 0
for batch_idx, (data, _) in enumerate(dataloader):
optimizer.zero_grad()
recon_batch, mean, logvar = model(data)
loss = model.loss_function(recon_batch, data, mean, logvar)
loss.backward()
train_loss += loss.item()
optimizer.step()
print(f"Epoch {epoch}, Loss: {train_loss / len(dataloader.dataset)}")
使用

https://civitai.com/models/70248/color101-vae
from PIL import Image
import numpy as np
import torch
from diffusers import AutoencoderKL
import requests
from io import BytesIO
# 设置设备并加载模型
device = 'cuda'
vae = AutoencoderKL.from_pretrained('runwayml/stable-diffusion-v1-5', subfolder='vae')
vae = vae.to(device)
# 定义编码函数
def encode_img_latents(imgs):
if not isinstance(imgs, list):
imgs = [imgs]
img_arr = np.stack([np.array(img) for img in imgs], axis=0)
img_arr = img_arr / 255.0
img_arr = torch.from_numpy(img_arr).float().permute(0, 3, 1, 2)
img_arr = 2 * (img_arr - 0.5)
latent_dists = vae.encode(img_arr.to(device))
latent_samples = latent_dists.latent_dist.sample()
latent_samples *= 0.18215
return latent_samples
# 定义解码函数
def decode_img_latents(latents):
latents = 1 / 0.18215 * latents
with torch.no_grad():
imgs = vae.decode(latents)
imgs = (imgs.sample / 2 + 0.5).clamp(0, 1)
imgs = imgs.detach().cpu().permute(0, 2, 3, 1).numpy()
imgs = (imgs * 255).round().astype('uint8')
pil_images = [Image.fromarray(image) for image in imgs]
return pil_images
# 拼接图像函数
def concat_image(im_list):
img_number = len(im_list)
if img_number == 0:
return None
dst = Image.new('RGB', (img_number * im_list[0].width, im_list[0].height))
for idx, im in enumerate(im_list, 0):
dst.paste(im, (idx * im.width, 0))
return dst
# 测试用例
pths = ["", ""] # 替换为实际图像 URL
for pth in pths:
response = requests.get(pth)
img = Image.open(BytesIO(response.content)).convert('RGB')
img = img.resize((256, 256))
img_latents = encode_img_latents(img)
dec_img = decode_img_latents(img_latents)[0]
concat_image([img, dec_img]).show() # 显示拼接的图像
VAE 与扩散模型
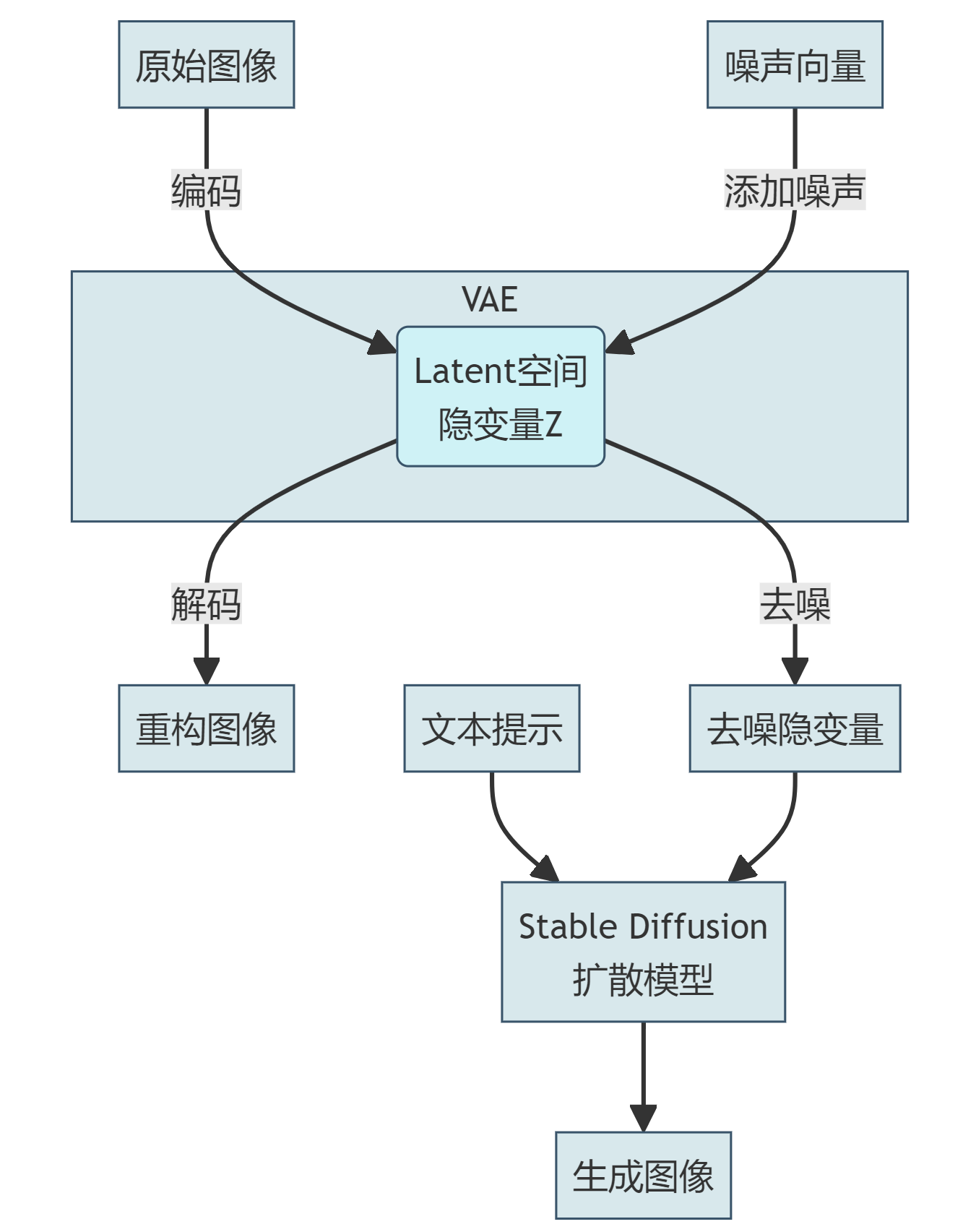
- 原始图像通过VAE编码器编码到Latent空间
- 在Latent空间添加噪声或去噪
- Stable Diffusion模型接受去噪的隐变量和文本提示作为输入
- 经过扩散过程生成新图像
VAE模块将图像表示到隐空间编码,以方便Stable Diffusion控制噪声过程。
-
增强数据表示能力:VAE 的潜在空间提供了一种紧凑的数据表示,但可能不足以捕捉所有复杂的数据变化。通过扩散模型,可以在这个空间中进一步加入细节和多样性。
-
改善生成质量:扩散模型能够生成极其逼真的图像。将这种能力应用于 VAE 的潜在空间,可以改善最终生成图像的质量。
-
降低计算复杂性:在潜在空间上进行操作相比于直接在高维图像空间上处理,可以降低计算复杂性和提高效率。
-
灵活性和创新:这种组合使用的方法展示了在深度学习和生成模型领域的创新和灵活性,通过不同技术的结合打开了新的可能性。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- jmeter,学这些重点就可以了
- 10分钟带你了解分布式系统的补偿机制
- 展望街机游戏的未来:融合、创新与可持续发展
- 热点聚焦 | 某知名演员病历遭泄露,医疗行业应如何为病人隐私贴好“封条”?
- 测试岗最好用的——十大软件测试工具
- USB-C接口给显示器带来怎样的变化?
- RabbitMQ Streams 详解
- 腾讯云活动服务器租用价格表(2024优惠活动报价)
- MySQL分库分表
- 如何通过VNC实现公网远程控制macOS设备