刷题第四十四天 300. 最长递增子序列 674. 最长连续递增子序列 718. 最长重复子数组
发布时间:2023年12月18日

class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# dp[j] 以第j个元素结尾的最长递增子序列长度
# i = 0:j 如果nums[j] > nums[i] 那么dp[j] = max(dp[j], dp[i] + 1)
dp = [1] * len(nums)
result = 1
for j in range(1, len(nums)):
for i in range(j):
if nums[j] > nums[i]:
dp[j] = max(dp[j], dp[i] + 1)
if dp[j] > result:
result = dp[j]
return resultdp数组的含义:以第j个元素结尾的最长递增子序列的长度
递推公式:如果第j个元素大于第i个元素,并且i < j。那么以第j个元素结尾的最长递增子序列的长度是所有的i的长度+1中最大的那个
dp[j] = max(dp[j], dp[i] + 1)
最后返回dp数组中的最大值
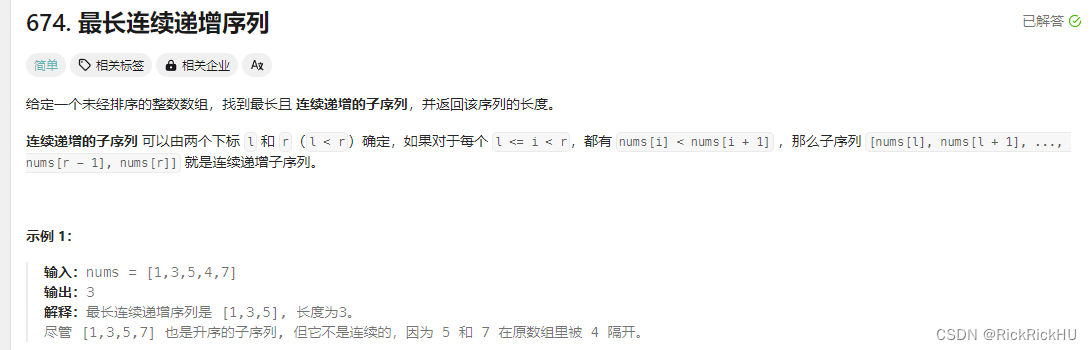
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
#dp[j] 以j结尾的最长连续递增子序列的长度
#dp[j] = dp[j - 1] + 1
dp = [1] * len(nums)
result = 1
for j in range(1, len(nums)):
if nums[j] > nums[j - 1]:
dp[j] = dp[j - 1] + 1
if dp[j] > result:
result = dp[j]
return result和前一题相比多了连续,所以不用比较所有小于j的i,只要比较前一个元素就可以了

class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
## dp[i][j] nums1中以i - 1结尾的子数组和nums2中以j - 1结尾的子数组中的公共子数组的最大长度
dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]
_max = 0
for i in range(1, len(nums1) + 1):
for j in range(1, len(nums2) + 1):
if nums1[i - 1] == nums2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
if dp[i][j] > _max:
_max = dp[i][j]
return _max## dp[i][j] nums1中以i - 1结尾的子数组和nums2中以j - 1结尾的子数组中的公共子数组的最大长度
文章来源:https://blog.csdn.net/qq_43211720/article/details/135011865
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 数据结构和算法的部分例题(力扣)
- C++基础-函数的默认参数详解
- flutter 文件上传封装
- 02 时间复杂度和空间复杂度
- Spring系列学习七、Spring的高级特性
- Win10下在Qt项目中配置SQlite3环境
- php的file_put_contents()是不安全的?
- 计算机组成原理-外部设备(输入 输出 显示器)
- 【触想智能】MES安卓工位一体机在制造业生产中备受青睐
- C# 图解教程 第5版 —— 第21章 异步编程