【学习笔记】1、数字逻辑概论

1.1 数字信号

• 数字信号，在时间和数值上均是离散的。
• 数字信号的表达方式：二值数字逻辑和逻辑电平描述的数字波形。

（1） 数字波形的两种类型

• 数值信号又称为“二值信号”。数字波形又称为“二值位形图”。

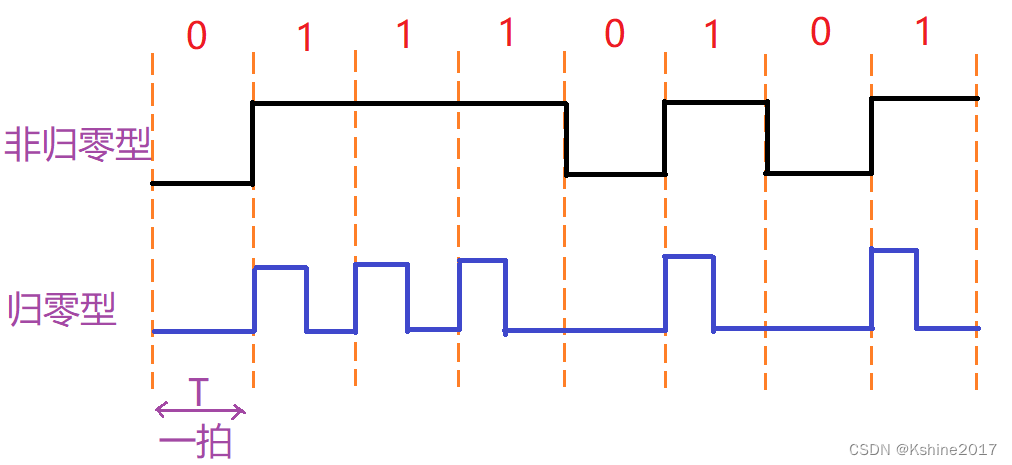
什么是一拍

• 一定的时间间隔T，称为1bit，或者1拍。

非归零型，数字波形

• 在一个时间拍内，高电平1，低电平0。
• 大多数数值信号都是非归零型。
• 非归零信号，每位数据占用一个位时间T。每秒钟传输数据的位数称为数据率（比特率）。

归零型，数值波形

• 在一个时间拍内，有脉冲表示1，无脉冲表示0。
• 只有作为时序控制信号使用的时钟脉冲是归零型。
  

（2）周期性和非周期性

• 周期性数字波形，常用周期T和频率f来描述。
  占空比=脉宽/周期
  $$q(\%)=\frac{t_w}{T}?100\%$$
• 占空比为50%的矩形脉冲，被称为“方波”。此时0和1交替出现，时间相同。

（3）实际数字信号波形

• 上升时间tr，脉冲幅度从10%-90%所经历的时间。几纳秒。
• 下降时间tf，脉冲幅度从90%-10%所经历的时间。几纳秒。
• 脉冲宽度tw，脉冲幅度50%的两个时间点的时间间隔。

（4）时序图

• 数字电路中，常用时序图或者脉冲波形图，来分析逻辑。

1.2 数制

（1）十进制

• 任何一个数，都可以用0123456789等是个数码中的一个或几个，按照一定的规律排列起来表示。
• 逢十进一。9+1=10（十）。
• 十进制是以10为基数的计数体制。
• 用数字电路来存储或者处理十进制数是很不方便的。因为构成数字电路的基本思路是把电路的状态与数码对应起来。

（2）二进制

• 只有0和1两个数码。
• 逢二进一。1+1=10（壹零）。
• 二进制是以2为基础的计数体制。
• 二进制的数字装置简单可靠，可用元件少。易于电路实现。
• 二进制的基本运算规则简单，运算操作方便。位数太多。

（3）十 - 二进制之间的转换

• 二进制转为十进制
  $$(1010110{)}_B=1?2^6+0?2^5+1?2^4+0?2^3+1?2^2+1?2^1+0?2^0=(86{)}_D$$

• 十进制转为二进制
  $$(37{)}_D=(100101{)}_B$$
  
  $$(0.706{)}_D=(0.101101001{)}_B$$
  要求误差不大于2^-10。
  

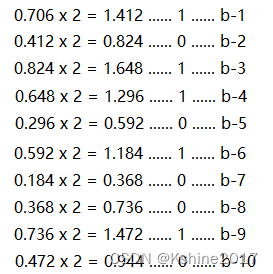
（4）十六进制和八进制

• 为了方便书写和记忆，在计算机资料中，常用十六进制或者八进制表示数值。与二进制之间转换容易。
• 十六进制有十六个数码，0123456789abcdef。
• 十六进制，逢十六进一。
• 十六进制是以16为基数的计数体制。
• 八进制有八个数码，01234567。
• 八进制，逢八进一。

1.3 二进制数的算术运算

（1）无符号二进制数的算术运算

• 二进制加法。
• 二进制减法。无符号减法计算，要求被减数一定要大于减数。
• 乘法运算和除法运算。可以使用类似于10进制乘除的方法。

（2）带符号二进制数的减法运算

• 十进制的补码表示。

• R表示基数，在二进制时，R=2，十进制时,R=10。

• N表示原码。

• n表示位数。
  $$(N{)}_{补}=R^n?N$$
  $$?N=(N{)}_{补}?R^n$$

• 以十进制为例，2的补码 = 10^1 - 2 = 8

• 以十进制为例，46的补码 = 10^2 - 46 = 54
  $$8?2=8+(2{)}_{补}?10=8+8?10=6$$

• 二进制的补码表示。

• 补码或者反码的最高位为符号位，正0，负1。

• 当二进制数为正数时，其补码，反码，原码相同。

• 当二进制数为负数时，对原码的数值位进行“取反加一”，得到补码。

1.4 二进制代码

• 数字系统中，信息可分为“数值”或者“文字符号”。
• 文字符号也可以使用二进制数码表示。这些数码不表示数量的大小，仅用于区别不同的事物。
• 称呼这样的二进制数码为“代码”。
• 编码： 以一定的规则编制“代码”的过程（十进制数值、字母、符号等实际含义 -> “代码”）。
• 译码：将“代码” 还原成实际含义的过程。

（1）二-十进制码

• 二-十进制码，Binnary Coded Decimal 。BCD码。
• 用4位二进制数，表示1位十进制数。
• 8421BCD码。“有权码”。自然二进制数的前10种组合。
• 2421BCD码。“有权码”。“自补码”。各数的“代码”，取反之后的“代码”，与原数“代码”关于9互补。
• 5421BCD码。“有权码”。
• 余3码。 “无权码”。8421+3得到“余三码”。具有“自补性”。
• 余3循环码。 “无权码”。“相邻性”。“格雷码”去掉首尾各自3种状态得到“余3循环码”

（2）格雷码

• 无权码，相邻只变一位。
• 模拟量 转换 成 数值时，用文字符号表示其数值。当模拟量发生微小变化而引发数值量从1位变化到相邻位时，格雷码可以保证只有一位变化。
• 细微的模拟量变化，如果发生多位位值变化的情况，在硬件实现时，不能保证多位同时翻转到最终值，会出现瞬间的错误码。
• 细微模拟量变化时，格雷码可以避免错误码的出现。

（3）ASCII码

• 使用7位二进制码，表示128个文字字符，包括十进制数码元，英文大小写，控制符，运算符，特殊符号。

1.5 二值逻辑变量与基本逻辑运算

• 逻辑运算 不是 算术运算。
• 逻辑变量可以用ABCxyz等字母表示。
• 逻辑变量的取值只能是0和1。表示完全对立的逻辑状态。

（1）与运算

• 运算符号：“·”点乘（可以省略）。或者“∧” 和“∩”。
  
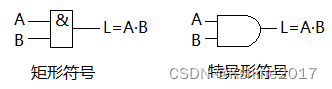
• 与逻辑真值表

A	B	L=A·B
0	0	0
0	1	0
1	0	0
1	1	1

（2）或运算

• 运算符号：“+” 。或者“∨”和“∪”。

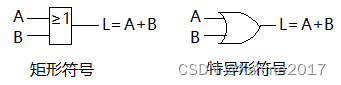
A	B	L=A+B
0	0	0
0	1	1
1	0	1
1	1	1

（3）非运算

• 运算符号：“￣”。或者“~”，“ ’ ’” ,“ ﹁”。
  

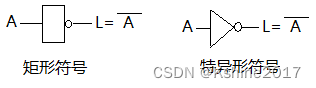
A	L=$\overline{\text{A}}$
0	1
1	0

（3）几种常用逻辑运算

• 与非
  

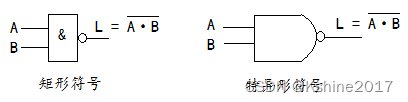
A	B	L=$\overline{A?B}$
0	0	1
0	1	1
1	0	1
1	1	0

• 或非
  

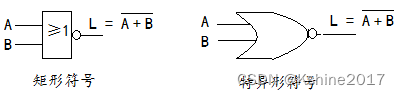
A	B	L=$\overline{A+B}$
0	0	1
0	1	0
1	0	0
1	1	0

• 异或
  

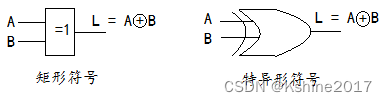
A	B	L= $\overline{A}$B+A$\overline{B}$=A⊕B
0	0	0
0	1	1
1	0	1
1	1	0

• 同或
  

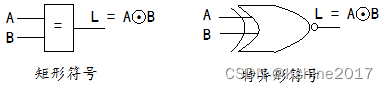
A	B	L= AB+$\overline{AB}$=A⊙B
0	0	1
0	1	0
1	0	0
1	1	1

1.6 逻辑函数及其表示方法

• 输入逻辑变量，只取0或1
• 输出逻辑变量，只取0或1
• 逻辑函数。
• 逻辑函数的描述方法有：真值表、逻辑函数表达式、逻辑图、波形图、卡诺图。

（1）真值表

A	B	L= AB+$\overline{AB}$=A⊙B
0	0	1
0	1	0
1	0	0
1	1	1

（2）逻辑表达式

L= AB+$\overline{AB}$=A⊙B

（3）逻辑图表示方法

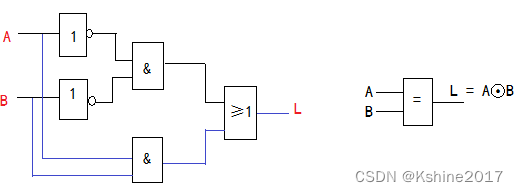
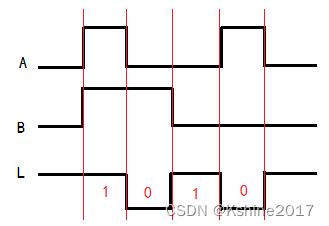
（4）波形图表示方法