最优化考试之共轭梯度法
一、共轭梯度法
1.前言
共轭梯度法在第一次时迭代的过程和最速下降法一样,但从第二步开始共轭梯度法就发生了变化,共轭梯度法的梯度下降方法不再是直接根据当前点计算?f(x)
2.问题条件
共轭梯度法的相关问题中的条件提炼出来如下,如果题目没有误差e,那就要求最后迭代出来的梯度值 ? f ( x ) {?f(x) } ?f(x) 接近0或等于0,一般自行选取e。
- 目标函数 ? f ( x ) {?f(x) } ?f(x)
- 初始点 x 0 {x}^{0} x0
- 误差 e
3.计算过程
- 选取初始点 x 0 {x}^{0} x0, k = 0 {k=0} k=0
- 计算 ? f {?f} ?f( x k {x}^{k} xk) ,若|| ? f {?f} ?f( x k {x}^{k} xk)|| < = e {<=e} <=e,停止迭代,输出结果 x k {x}^{k} xk
- 第一次的梯度 d = ? ? f ( x k ) {d=-}?f(x^k) d=??f(xk),跳至第6步
- 除第一次迭代外,要计算的系数b如下
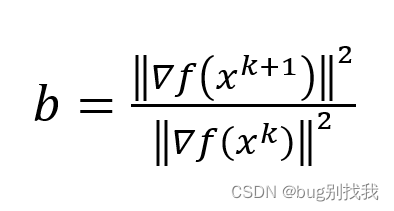
- d k + 1 = ? ? f ( x k ) + b ? d k d_{k+1}=-?f(x^k)+b*d_k dk+1?=??f(xk)+b?dk?
- 下一个迭代点 x k + 1 {x}^{k+1} xk+1= x k x^k xk+ t k t_k tk?* d k + 1 d_{k+1} dk+1?
- 设函数 g ( t k ) = f ( {g(t_k)=f(} g(tk?)=f( x k + 1 {x}^{k+1} xk+1),对 g ( t k ) {g(t_k)} g(tk?)求导,计算当 g ′ ( t k ) = 0 {g'(t_k)=0} g′(tk?)=0时步长 t k {t_k} tk?的值;因此推导出 x k + 1 {x}^{k+1} xk+1,k=k+1,跳至第2步
4.例子

4.1 第一次迭代
和最速下降法一样,先计算梯度下降方向 d 0 = ? ? f ( x 0 ) = [ 1 , ? 1 ] T d_0=-?f(x^0)=[1,-1]^T d0?=??f(x0)=[1,?1]T
下一个迭代点 x 1 = x 0 + d 0 ? t 0 {x^1=x^0+d_0*t_0} x1=x0+d0??t0?
设函数 g ( t 0 ) = f ( x 0 ) = t 0 2 ? 2 ? t 0 g(t_0)=f(x^0 )={t_0}^2-2*t_0 g(t0?)=f(x0)=t0?2?2?t0?
对 g ( t 0 ) {g(t_0)} g(t0?)求导,当 g ′ ( t 0 ) = 0 {g'(t_0)=0} g′(t0?)=0时, t 0 = 1 {t_0=1} t0?=1,代入求得 x 1 = [ 1 , ? 1 ] T {x^1 =[1,-1]^T } x1=[1,?1]T
4.2 第二次迭代
先计算系数
b
=
1
b=1
b=1
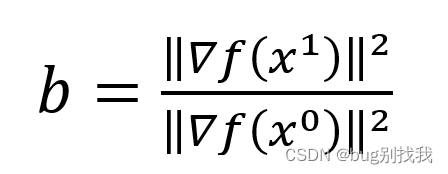
梯度下降方向
d
1
=
?
?
f
(
x
1
)
+
b
?
d
0
=
[
2
,
0
]
T
d_1=-?f(x^1)+b*d_0=[2,0]^T
d1?=??f(x1)+b?d0?=[2,0]T
下一个迭代点 x 2 = x 1 + d 1 ? t 1 {x^2=x^1+d_1*t_1} x2=x1+d1??t1?
设函数 g ( t 1 ) = f ( x 2 ) = 4 ? t 1 2 ? 2 ? t 1 ? 1 g(t_1)=f(x^2 )={4*t_1}^2-2*t_1-1 g(t1?)=f(x2)=4?t1?2?2?t1??1
对 g ( t 1 ) {g(t_1)} g(t1?)求导,当 g ′ ( t 1 ) = 0 {g'(t_1)=0} g′(t1?)=0时, t 1 = 1 / 4 {t_1=1/4} t1?=1/4,代入求得 x 2 = [ 3 / 2 , ? 1 ] T {x^2 =[3/2,-1]^T } x2=[3/2,?1]T
此时 ? f ( x 2 ) = 0 < e ?f(x^2)=0<e ?f(x2)=0<e,因此 x 2 x^2 x2为最优解点,最优解为 f ( x 2 ) = 5 / 4 f(x^2)=5/4 f(x2)=5/4
PS:
后续迭代按照第二次迭代的方法依次计算即可
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- vue3 父传子 子传父
- 来瞅瞅Java 11都有啥新特性
- 好用的硬盘分区工具,傲梅分区助手 V10.2
- TMC4361A编码器反馈的可能调节选项
- java使用keytool生成证书
- 深入探索JavaScript中实用而高级的Rest参数和Spread语法
- Python MySQL 数据库查询:选择数据、使用筛选条件、防止 SQL 注入
- CISSP认证计算机化自适应考试(CAT)及常见问题解答
- Go反射问题记录panic: reflect: call of reflect.Value.Elem on struct Value [recovered]
- Python(32):字符串转换成列表或元组,列表转换成字典小例子