回溯算法篇-02：括号生成

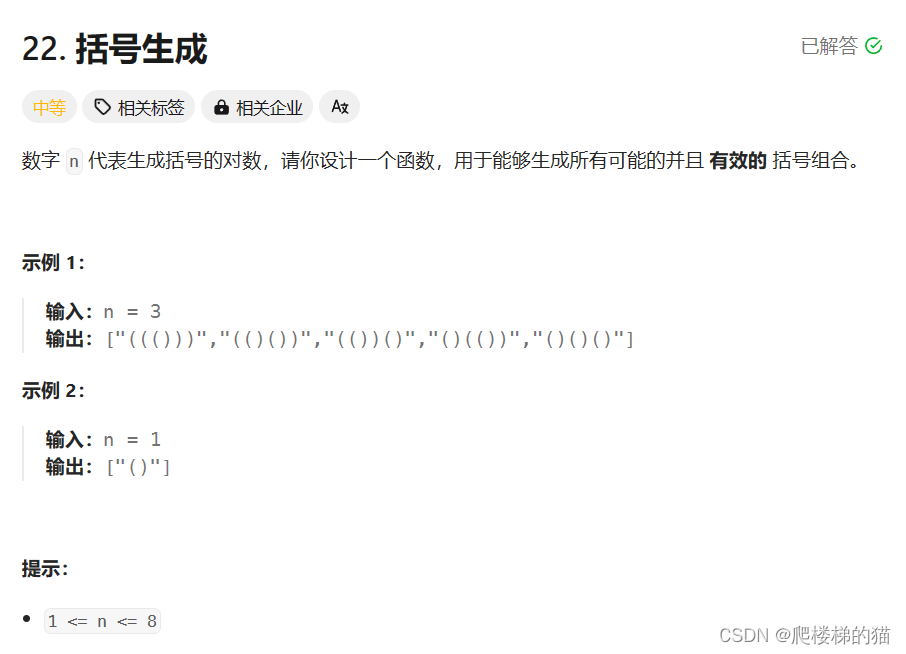
力扣22、括号生成

?题目分析

对于括号类问题，有以下两个性质：

• 一个“合法”的括号组合中，左括号数量一定等于右括号数量
• 对于一个 “合法” 的括号字符串组合 p ，必然对于任何 0 <= i <= len(p) 都有：子串 p[0...i] 中左括号的数量都大于或等于右括号的数量

这道题从回溯算法的视角来看，可以改写为

“现在有?2n?个位置，每个位置可以放置字符?(?或者?)，组成的所有括号组合中，有多少个是合法的？”

回溯算法就是遍历所有选择得出结果。所以我们需要打印所有的括号组合，然后根据筛选其中合法的括号组合即可

对于路径中的每一个位置，我们都能做出两个选择：“放一个左括号”、“放一个右括号”

解题框架

最终代码

public List<String> generateParenthesis(int n) {
    if (n == 0) return new ArrayList<>();
    // 记录所有合法的括号组合
    List<String> res = new ArrayList<>();
    // 回溯过程中的路径
    StringBuilder track = new StringBuilder();
    // 可用的左括号和右括号数量初始化为 n
    backtrack(n, n, track, res);
    return res;
}

// 可用的左括号数量为 left 个，可用的右括号数量为 rgiht 个
void backtrack(int left, int right, 
            StringBuilder track, List<String> res) {

    //设立结束条件

    // 若左括号剩下的多，说明不合法
    if (right < left) return;
    // 数量小于 0 肯定是不合法的
    if (left < 0 || right < 0) return;
    // 当所有括号都恰好用完时，得到一个合法的括号组合
    if (left == 0 && right == 0) {
        res.add(track.toString());
        return;
    }
    
    // 尝试放一个左括号
    track.append('('); // 选择
    backtrack(left - 1, right, track, res);
    track.deleteCharAt(track.length() - 1); // 撤消选择

    // 尝试放一个右括号
    track.append(')'); // 选择
    backtrack(left, right - 1, track, res);
    track.deleteCharAt(track.length() - 1); // 撤消选择
}

?