【论文阅读笔记】Pre-trained Universal Medical Image Transformer
Luo L, Chen X, Tang B, et al. Pre-trained Universal Medical Image Transformer[J]. arXiv preprint arXiv:2312.07630, 2023.【代码开源】
【论文概述】
本文介绍了一种名为“预训练通用医学图像变换器(Pre-trained Universal Medical Image Transformer,简称PUMIT)”的新型算法,该算法旨在解决标记医学图像数据稀缺的问题。作者通过自监督学习方法,特别是掩码图像建模(Masked Image Modeling,MIM)和视觉标记重构,利用大量未标记的医学影像数据。本文提出了一个空间自适应卷积(Spatially Adaptive Convolution,SAC)模块,以适应输入图像的体素间距,从而有效处理各种成像方式和空间属性的医学图像。此外,作者还改进了视觉标记器,使其输出概率软标记,以提高模型的鲁棒性。整体而言,这项工作通过在55个公共医学图像数据集(包括超过900万个2D切片和48000个3D图像)上预训练通用视觉标记器和视觉变换器(ViT),在下游医学图像分类和分割任务中展示了出色的性能和标记效率。
【关键创新点总结】
- 空间自适应卷积(SAC)模块:这是一种新型的卷积方法,能够根据医学图像的体素间距自适应调整卷积参数。SAC模块使得模型能够有效处理具有不同空间属性的医学图像,特别是在处理具有高度各向异性的图像时。
- 通用视觉标记器(Universal Visual Tokenizer):这种标记器能够将医学图像转换成一系列的视觉标记,为后续的深度学习模型提供了一种更高效的信息表达方式。
- 扩展先验分布正则化(Extended Prior Distribution Regularization):这是一种改进的正则化技术,通过考虑软标记表示中的不确定性,它有助于提高模型在处理复杂医学图像时的稳定性和准确性
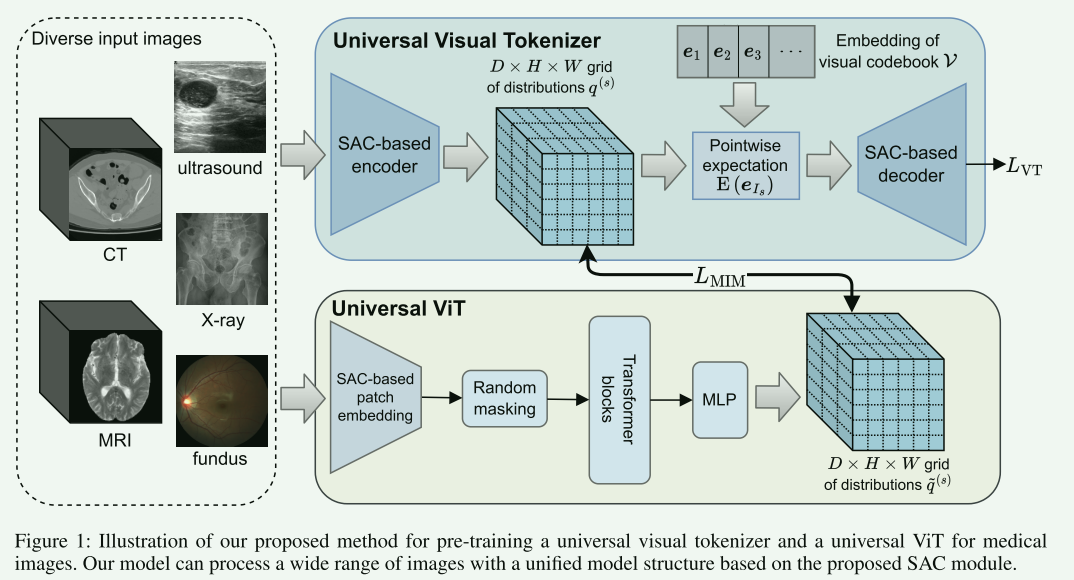
【1.引言部分概述】
在本文的引言部分中,作者着重强调了深度学习在医学图像分析领域的重要性,特别是在疾病诊断和治疗计划中的应用。然而,这一领域面临的主要挑战之一是高质量标记医学数据的稀缺性。为了解决这一问题,作者提出了自监督学习的方法,它可以通过设计自监督的预文本任务来从大量未标记的数据中学习表示。
引言部分还提到,尽管存在大量未标记数据,但医学图像在成像方式(例如CT、MRI、超声等)和空间属性(如2D和3D空间维度、不同的体素间距和空间形状)方面的高度异质性,使得使用统一的模型结构处理所有类型的医学图像变得非常困难。传统的模型通常设计为处理具有单一空间属性的图像。因此,大多数先前的工作只能利用具有相似空间属性的医学图像数据,这限制了预训练数据的数量和多样性。
最后,作者指出了计算机视觉领域的视觉变换器(ViT)的最新进展,这为处理具有多样空间属性的医学图像提供了一种有前景的解决方案。本文的目标是通过引入空间自适应卷积(SAC)模块和改进的视觉标记器,预训练一个能够处理广泛医学图像的通用视觉变换器,以解决在医学图像分析中标记数据稀缺的问题。
本文的主要贡献如下:
- 空间自适应卷积(SAC)模块的提出:作者开发了一种新型的SAC模块,它能够根据输入图像的体素间距自适应调整卷积参数。这种方法使得模型能够有效处理具有不同成像方式和空间属性的广泛医学图像。
- 构建通用视觉标记器和视觉变换器(ViT):利用SAC模块,作者构建了一个通用的视觉标记器和一个通用的ViT,这些模型适用于预训练并能有效处理各种医学图像。
- 概率软标记的引入:为了增强视觉标记器在掩码图像建模(MIM)中重建目标的鲁棒性,作者提出了从离散标记(VQ-VAE)到概率软标记的概念,以缓解确定性量化中的代码本崩溃问题,并通过扩展的先验分布正则化来提高学习分布的多样性和锐度。
- 大规模预训练:该模型在55个公共医学图像数据集上进行了预训练,这些数据集包含超过9百万个2D切片和超过48,000个3D图像,代表了目前已知最大、最全面和最多样化的用于预训练3D医学图像模型的数据集。
- 在下游医学图像任务中的优异性能:作者对预训练的模型在医学图像分类和分割任务上进行了微调,实验结果表明,该模型在这些任务上展现出了优越的性能和提高的标签效率。
【2.核心贡献Spatially Adaptive Convolution详细解读】:
空间自适应卷积(SAC)模块是为了解决医学图像分析中一个关键问题而设计的:即不同医学图像(如CT、MRI、超声图像)在空间分辨率和体素间距方面的显著差异。传统的卷积神经网络(CNN)在处理这些图像时可能会遇到困难,因为它们通常是针对特定类型的图像优化的,而不是为处理各种不同的空间属性设计的。
SAC模块的工作机制
SAC模块的核心思想是自适应地调整卷积操作,以适应输入图像的体素间距。这是通过以下步骤实现的:
- 体素间距的识别:SAC首先分析输入图像的体素间距。体素间距是医学图像中体素的物理尺寸,不同的成像技术(如CT、MRI)和不同的扫描设置会产生不同的体素间距。
- 调整卷积参数:根据识别的体素间距,SAC调整其卷积核的大小和步长。在具有较大体素间距的图像中,SAC可能会使用更大的卷积核来覆盖更广泛的区域,从而捕获更大范围的上下文信息。相反,在具有较小体素间距的高分辨率图像中,SAC会使用较小的卷积核,以更精细地捕捉细节。
- 自适应特征提取:通过这种方式,SAC能够更有效地提取各种医学图像中的特征。对于高分辨率图像,它可以更精确地捕捉细节;对于低分辨率或不均匀采样的图像,它可以通过较大的卷积核捕获更多的上下文信息。
SAC模块的优势
SAC模块的主要优势在于其灵活性和适应性。它能够针对不同类型的医学图像动态调整卷积操作,从而提高模型处理不同空间属性图像的能力。这种方法对于提高医学图像分析的精度和效率至关重要,特别是在涉及多种成像技术和不同解剖区域的图像时。
各向异性的影响
在本文中提到的“度量各向异性”(degree of anisotropy)是一个关键概念,用于描述医学图像中体素的空间分布特性。在医学成像领域,各向异性是指图像在不同方向上分辨率的不一致性。具体来说,在三维医学图像中,体素可能在垂直于切片的方向(通常是Z轴)上的尺寸与在切片内(即X轴和Y轴)的尺寸不同。这种不一致性导致图像在不同方向上的空间分辨率不同,即表现出各向异性。
- 分辨率差异:在具有高度各向异性的图像中,体素在不同方向上的大小差异可能很大。例如,MRI或CT扫描中沿Z轴的体素尺寸可能比X轴和Y轴上的大得多。
- 图像解释:这种分辨率的不一致性可能影响图像的解释和分析,尤其是在进行三维重建或体素级分析时。
- 图像处理挑战:对于深度学习模型而言,处理高度各向异性的图像比处理各向同性(即在所有方向上具有相同分辨率)的图像更具挑战性。
各向异性的度量
论文中定义了公式 D A = max ? { 0 , ? log ? 2 s slice? s plane? ? } \mathrm{DA}=\max \left\{0,\left\lfloor\log _{2} \frac{s_{\text {slice }}}{s_{\text {plane }}}\right\rfloor\right\} DA=max{0,?log2?splane??sslice????},用于量化医学图像在不同维度上的空间分辨率差异,特别是在处理3D图像(如CT或MRI扫描)时。
- s s l i c e s_{slice} sslice?:表示沿着切片方向(通常是Z轴)的体素尺寸。
- s p l a n e s_{plane} splane?:表示在切片平面内(通常是X轴和Y轴)的体素尺寸。
- 公式作用:这个公式的目的是为了量化图像在切片方向与平面方向上体素尺寸的相对差异,从而帮助SAC模块调整其处理策略以适应这种各向异性。例如,如果切片方向(Z轴)上的体素尺寸远大于平面内(X轴和Y轴)的体素尺寸,DA的值将会较大,反映出图像的高度各向异性。这种信息对于指导SAC模块如何调整其卷积核大小和步长至关重要,以有效处理具有不同空间分辨率的3D医学图像。
空间自适应卷积(SAC)的三个变体
- Downsampling:卷积核大小和步幅都是 2 k 2^k 2k,其中 k k k是非负整数。沿着深度维度的卷积权重沿着通过求和池化(sum pooling)被减小到 2 max ? { k ? D A , 0 } 2^{\max \{k-\mathrm{DA}, 0\}} 2max{k?DA,0}的大小,并且深度维度的步幅类似地被调整为 2 max ? { k ? D A , 0 } 2^{\max \{k-\mathrm{DA}, 0\}} 2max{k?DA,0},输出特征图的间距乘以调整后的步幅。降采样可以使图像在不同方向上的分辨率更加一致。例如,如果一个图像在垂直方向(比如Z轴)上的分辨率远高于水平方向(X轴和Y轴),通过降采样,可以使这三个方向的分辨率更加均衡。
-
3
3
3^3
33 convolution:
- 卷积核尺寸为3,深度维度上的步长为1,这意味着在进行卷积操作时,使用的卷积核(或过滤器)在每个维度(宽度、高度和深度)上的尺寸都是3个单位长度。同时,当卷积核沿着图像的深度方向移动时,它每次移动1个单位距离(即步长为1);
- 如果DA(度量各向异性)大于0:DA是用来量化图像在不同维度上分辨率差异的指标。当DA的值大于0时,表明图像在不同方向上的分辨率存在明显差异,即图像显示出一定程度的各向异性。
- 通过求和池化沿深度维度减小卷积权重:如果图像显示出各向异性(即DA > 0),则会对卷积核在深度维度上的权重进行调整。具体来说,是通过“求和池化”(sum pooling)操作,将卷积核在深度维度上的权重整体减小,使其在这一维度上的尺寸缩减到1。这样的处理有助于适应图像在深度方向上的分辨率特性,从而在保持重要信息的同时降低计算复杂度。
- Upsampling:就是下采样的逆过程,用的卷积核调整方式也相同:
- 转置卷积核尺寸和步长:在上采样过程中,转置卷积(transposed convolution,有时也称为反卷积)被用来增加图像的尺寸。转置卷积核的尺寸和步长都被设置为 2 k 2^k 2k,转置卷积核在所有维度上的大小和移动步长是相等的,并且是2的 k k k次幂。
- 深度维度上的卷积核尺寸和步长调整:在深度维度上,转置卷积核的尺寸和步长被特别调整为 2 min ? { k , D A 0 ? D A } 2^{\min \left\{k, \mathrm{DA}_{0}-\mathrm{DA}\right\}} 2min{k,DA0??DA}。这里, D A 0 DA_0 DA0? 是输入图像的各向异性度量(DA),而 DA 是当前层的各向异性度量。这样的调整考虑了输入图像和当前处理层在深度维度上的各向异性差异。
- 输出特征图的间距调整:由于上采样会增加图像尺寸,因此输出特征图(output feature map)的间距(即体素或像素之间的物理距离)会根据调整后的步长而相应减小。
SAC中使用的SUM Pooling的说明
-
sum Pooling的工作原理:
- 区域选择:sum pooling操作首先将输入的特征图分割成若干非重叠的小区域。这些区域的大小通常是预先定义的,比如 2×2或 3×3。
- 求和操作:在每个小区域内,sum pooling会计算该区域内所有值的总和。
- 输出特征图:每个区域的求和结果形成了一个新的、更小尺寸的特征图。这个特征图在每个对应区域只有一个值,即原区域内所有值的总和。
-
Sum Pooling与其他池化方法的比较:
- Max Pooling(最大值池化):最大值池化选择每个区域内的最大值作为输出。它非常有效于捕捉图像中的纹理和模式,是最常用的池化方法之一。
- Average Pooling(平均值池化):平均值池化计算每个区域内值的平均值。它有助于平滑特征图,但可能会使特征图丢失一些重要信息。
- Sum Pooling(求和池化):与平均值池化类似,但不是计算平均值,而是计算总和。这可以保留区域内的更多信息,但也可能导致特征值的范围变大。
-
Sum Pooling的应用场景:
Sum pooling适用于那些需要保留特征图区域内尽可能多信息的场景。尽管在实际应用中不如最大值池化或平均值池化普遍,但在某些特定的应用中,如需要保留更多原始特征信息的任务,sum pooling可能会是一个更好的选择。此外,在处理那些特征值本身代表某种累积量(如总能量、总密度等)的数据时,sum pooling也可能特别有效。
【3.Universal Visual Tokenizer】
将常规CNN中的卷积和反卷积替换为文中提出的SAC变体
【4.Universal ViT】
ViT的Patch Embedding将输入图像划分为一系列不重叠的Patch ,并通过线性投影将每个Patch 映射到嵌入向量。这个过程相当于使用具有相同内核大小和步幅的下采样卷积处理输入图像,并平坦化卷积输出的空间维度。直接使用本文提出的Downsampling替代。
【5.论文核心贡献2-Soft Token Representation】
这个概念类似于Label Smoothing,用于提升模型鲁棒性。
Soft Token Representation的基本概念:
- 软标记:在软标记表示中,图像的每个部分或区域被转换成一个概率分布,而不是一个单一的、离散的标记。这种表示捕捉了每个区域可能属于不同类别或具有不同特征的不确定性。
- 概率分布:每个软标记对应于一个概率分布,表示图像该部分属于不同类别的概率。这样,图像的每个区域不再被简单地分类为某一特定类别,而是以一系列概率值来描述,反映了其可能属于各种类别的程度。
Soft Token Representation在医学图像中的应用:
- 特征提取:在医学图像分析中,软标记表示可以更丰富地捕捉图像特征,特别是在存在模糊边界或不确定性较高的区域。
- 增强模型鲁棒性:由于软标记包含了更多信息和潜在的类别关联,它可以提高模型对图像变化的适应性和鲁棒性。
- 处理不确定性:医学图像常常包含模糊不清或难以区分的区域。软标记表示通过允许这些区域映射到概率分布,而不是单一的类别,更好地处理了这种不确定性。
Soft Token Representation的优势:
- 增强的信息表达:相比于传统的硬标记表示,软标记能够提供更多的信息和细节,特别是在图像的复杂区域。
- 灵活性:软标记方法在处理各种医学图像时更加灵活,能够适应图像中的不确定性和多样性。
- 提高精确度:在一些情况下,软标记表示能够提高医学图像分类和识别的精确度。
【6.论文核心贡献2-Extended Prior Distribution Regularization详细解读】
-
扩展先验分布正则化的背景:
- 软标记表示的低代码本利用率:作者发现仅使用软标记表示时,代码本(codebook,一种用于编码特征的工具)的利用率仍然较低。代码本利用率低意味着许多预定义的特征(或标记)没有被充分使用,这可能限制了模型学习到的特征的多样性。
-
先验分布正则化的方法:
- 先前研究的方法:在之前的研究中,先验分布正则化通过计算所有样本离散标记的代码本上的独热分布的平均值(称为 p p o s t p_{post} ppost?),并最小化 p p o s t p_{post} ppost? 与均匀分布 p p o s t p_{post} ppost?之间的KL散度(Kullback-Leibler divergence)来实现。
- 应用于软标记表示:这种技术可以轻松地泛化到软标记表示上,通过用一般类别分布替换一热分布来实现。
-
软标记表示下的构造性解释:
- 编码器输出的网格:假设编码器输出一个 D×H×W*的标记分布网格。 G D , H , W G_{D, H, W} GD,H,W? 表示网格内所有单元格的离散坐标集。
- 随机变量定义:对于网格上的每个位置 s ∈ G D , H , W s \in G_{D, H, W} s∈GD,H,W?,定义一个随机变量 I s I_s Is? 表示在 s s s位置的代码本索引,及其分布 q ( s ) q(s) q(s)。同时,定义另一个随机变量 S S S*,表示网格上的随机位置,其在 G D , H , W G_{D, H, W} GD,H,W? 上均匀分布。
- 网格上标记分布的平均值:网格上所有标记分布的平均值正好是 I s I_s Is?的分布。这意味着,通过考虑网格上每个位置的标记分布,可以得到整个网格的平均分布特性。
-
分布接近均匀分布的情况:
- 分布接近均匀分布时的直观解释:当 I s I_s Is? 的分布接近均匀分布时,这意味着每个标记(token)在随机采样位置出现的概率几乎相同。这种情况有利于增加学习到的分布的多样性,因为它避免了对特定标记的过度偏好。
- 多样性的好处:通过确保标记在不同位置以接近相等的概率出现,模型能够更好地探索和表示数据的不同方面,从而提高其泛化能力和鲁棒性。
-
避免分布全部崩溃到均匀分布:
- 引入新的目标:为了防止所有分布都崩溃成均匀分布(即失去区分度),作者引入了一个新的目标,即最大化 E [ D K L [ q ( S ) ∥ p prior? ] ] E\left[\mathrm{D}_{\mathrm{KL}}\left[q(S) \| p_{\text {prior }}\right]\right] E[DKL?[q(S)∥pprior??]]。这里的 E E E 表示期望值, D K L D_{KL} DKL? 表示Kullback-Leibler散度。
- 增加分布的锐度:通过最大化 q ( S ) q(S) q(S)(模型预测的分布)与 p p r i o r p_{prior} pprior?(先验分布,这里是均匀分布)之间的KL散度,可以增加学习到的分布的锐度。这意味着每个标记的分布将更加集中,而不是平坦和模糊。
-
扩展先验分布正则化的实现:
- KL散度的表达:对于任何分布 p p p, D K L ( p ∥ p prior? ) \mathrm{D}_{\mathrm{KL}}\left(p \| p_{\text {prior }}\right) DKL?(p∥pprior??)可以表达为 ? H ( p ) + ln ? ∣ V ∣ -H(p)+\ln |V| ?H(p)+ln∣V∣,其中 H ( p ) H(p) H(p) 是分布 p p p 的熵,定义为, ? ∑ i = 1 ∣ V ∣ p i ln ? p i -\sum_{i=1}^{|V|} p_{i} \ln p_{i} ?∑i=1∣V∣?pi?lnpi?而 ∣ V ∣ |V| ∣V∣是可能标记的数量。
- 最小化的目标:因此,扩展先验分布正则化可以通过最小化损失函数中包含上述KL散度的目标来实现。
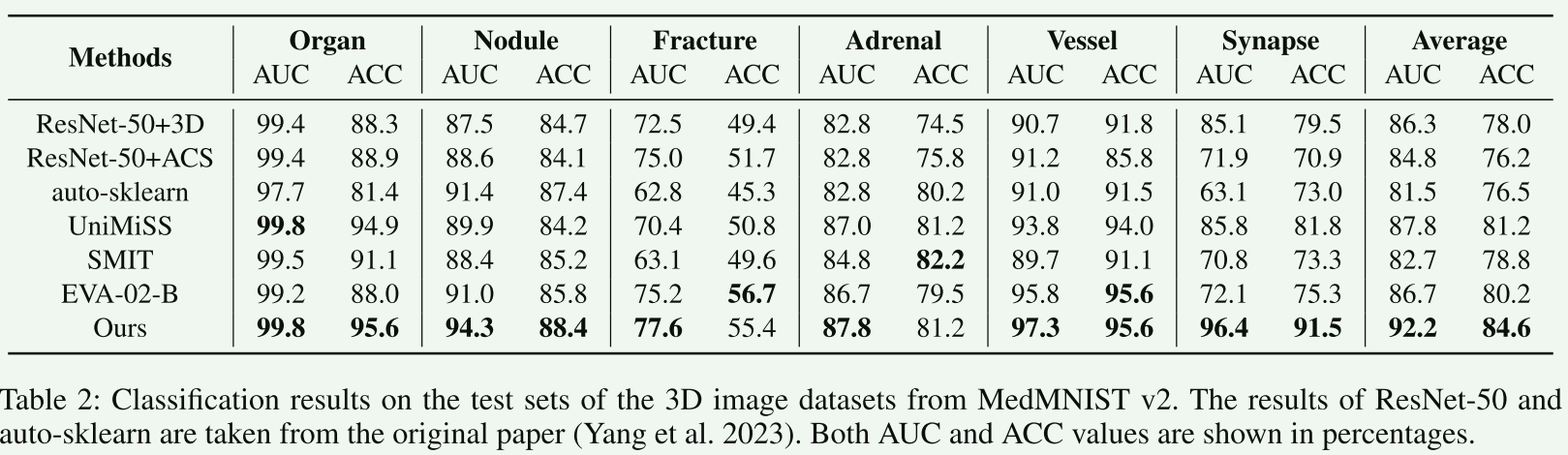
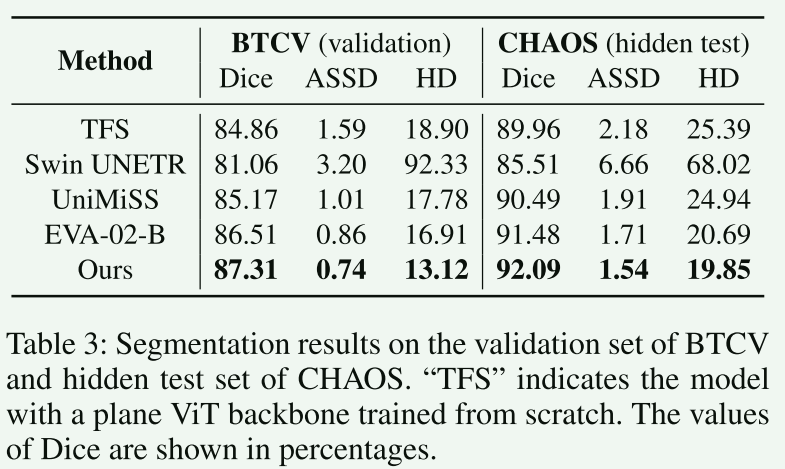
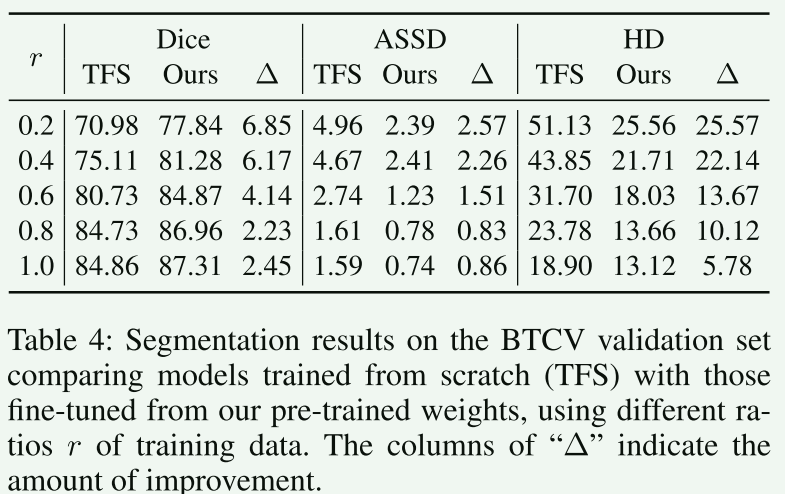
【7.实验和对比】
这部分本文从略,只是简单列举

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 基于springboot +vue +element-ui 技术开发的SaaS智慧校园云平台源码
- 学习中的零碎的记录
- 爬虫工作量由小到大的思维转变---<第二十二章 Scrapy开始很快,越来越慢(诊断篇)>
- 算法的效率度量?法有哪些?
- 年度大盘点:AIGC、AGI、GhatGPT震撼登场!揭秘人工智能大模型的奥秘与必读书单
- 【网络安全】上网行为代理服务器启用Alerts
- 如何优化亚马逊SEO,提升商品排名?
- 使用淘宝APIitem_get获取商品详情的技巧
- 数据结构实验1:栈和队列的应用
- 《web课程设计》使用HTML+CSS制作大学生校园二手交易网站