【数据结构】二叉树相关oj题（一）

目录

1、二叉树的构建及遍历

1.1、题目介绍

1.2、解题思路

1.3、代码描述

1.4、完整代码

?2、二叉树的层次遍历

2.1、题目介绍

2.2、解题思路

2.3、代码描述

2.4、完整代码?

?

1、二叉树的构建及遍历

1.1、题目介绍

原题链接：KY11 二叉树构建及遍历_牛客题霸_牛客网 (nowcoder.com)

示例1：

输入：abc##de#g##f###

输出：c b e g d f a

1.2、解题思路

根据题意可知，读入的字符串是一串先序遍历字符串，那么根据字符串创建二叉树也就需要遵循先序遍历进行创建。

1.3、代码描述

首先自行定义一个TreeNode类

class TreeNode {
    public char val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(char val) {
        this.val = val;
    }
}

因为递归创建，为了确保str能够正常遍历结束，因此这里定义一个成员变量 i 用于记录str当前访问的位置。

char ch = str.charAt(i++); 此时当ch不为#时再创建节点root，并且对左孩子和右孩子分别进行递归创建。

    public static int i = 0;

    public static TreeNode createTree(String str) {
        if(str == null) {
            return null;
        }
        TreeNode root = null;
        char ch = str.charAt(i++);
        if(ch != '#') {
            root = new TreeNode(ch);
            root.left = createTree(str);
            root.right = createTree(str);
        } 
        return root;
    }

最后执行中序遍历将结果打印出来即可

    public static void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }

1.4、完整代码

import java.util.Scanner;

class TreeNode {
    public char val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(char val) {
        this.val = val;
    }
}

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        String str = in.nextLine();
        //创建二叉树
        TreeNode root = createTree(str);
        //中序遍历二叉树
        inOrder(root);
    }

    public static int i = 0;

    public static TreeNode createTree(String str) {
        if(str == null) {
            return null;
        }
        TreeNode root = null;
        char ch = str.charAt(i++);
        if(ch != '#') {
            root = new TreeNode(ch);
            root.left = createTree(str);
            root.right = createTree(str);
        } 
        return root;
    }

    
    public static void inOrder(TreeNode root) {
        if(root == null) {
            return;
        }
        inOrder(root.left);
        System.out.print(root.val + " ");
        inOrder(root.right);
    }
}

?2、二叉树的层次遍历

2.1、题目介绍

原题链接：102. 二叉树的层序遍历 - 力扣（LeetCode）

?示例1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例2：

输入：root = [1]
输出：[[1]]

示例3：?

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

2.2、解题思路

????????层次遍历需要使用到队列，利用队列先进先出的特性使遍历能够从上到下，从左到右顺序遍历。该题唯一的难点就是返回值的规范。

????????题目中要求返回的是List<List<Integer>>，从示例中可以看出，每一层的节点分别使用有一个List来存储，这就要求我们不仅需要实现层序遍历，还需要将遍历结果按照层数划分。

2.3、代码描述

首先实现层次遍历，判断root不等于null后执行以下代码，将root入队之后，观察队列状况，当队列不为空时将节点出队，并判断出队节点是否存在左右节点，如果存在则入队。依次执行循环后最终得到打印结果就为层次遍历结果。

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            //此处对cur.val执行打印操作，打印的顺序就是层次遍历顺序
            System.out.print(root.val + " ");
            if(cur.left != null) {
                queue.add(cur.left);
            }
            if(cur.right != null) {
                queue.add(cur.right);
            }
        }

假设二叉树的结构如下：

?

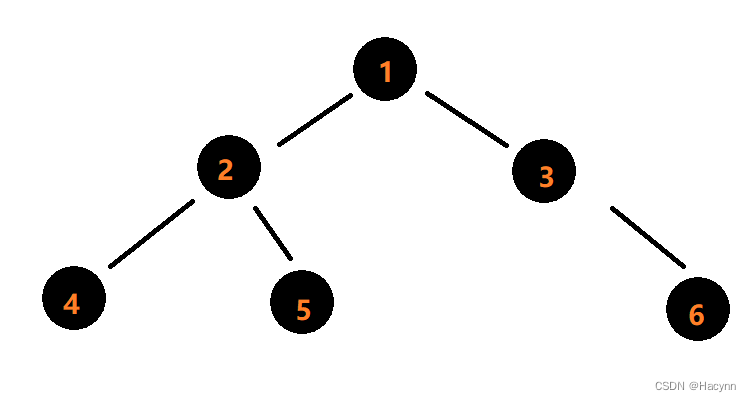
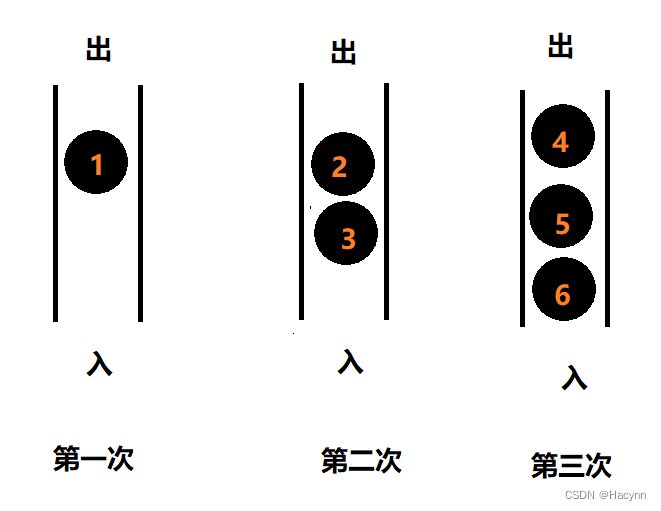
????????通过画图可以观察到，当将1入队后，此时队长为1。然后1出队后将2，3入队?，此时队长为2。然后2出队4，5入队，3出队6入队，此时队长为3。

????????相信大家都看出规律了，即每当执行完一组入队操作之后，此时队列的长度就等于层数个数。根据这个规律，我们可以在每次while循环的开始计算此时队列的长度，用于记录该层需要出队的次数，从而确定每一层的节点，并将其存放到list中，最后当while循环结束时将list添加到retList中。

具体优化后的代码如下文的【完整代码】?

2.4、完整代码?

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> retList = new LinkedList<>();
        if(root == null) {
            return retList;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()) {
            List<Integer> list = new LinkedList<>();   //存放一层节点的集合List
            int size = queue.size();   //每次计算队列长度

            while(size --> 0) {   //每完成一次出队，size自减1
                TreeNode cur = queue.poll();
                list.add(cur.val);   
                if(cur.left != null) {
                    queue.add(cur.left);
                }
                if(cur.right != null) {
                    queue.add(cur.right);
                }
            }
            retList.add(list);  //将一层的节点添加到返回集合retList中
        }
        return retList;
    }
}

?

【博主推荐】
【计算机网络】虚拟路由冗余（VRRP）协议原理与配置-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/134697735?spm=1001.2014.3001.5502

【JavaSE】基础笔记 - 异常（Exception）-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/134564361?spm=1001.2014.3001.5502

?【计算机组成原理】知识点巩固 - 存储器概述_半字地址和字节地址-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/134482974?spm=1001.2014.3001.5502

如果觉得作者写的不错，求给博主一个大大的点赞支持一下，你们的支持是我更新的最大动力！

如果觉得作者写的不错，求给博主一个大大的点赞支持一下，你们的支持是我更新的最大动力！

如果觉得作者写的不错，求给博主一个大大的点赞支持一下，你们的支持是我更新的最大动力！

?