【Java数据结构】04-图（Prim,Kruskal,Dijkstra,topo）

5 图

推荐辅助理解

1. 【视频讲解】bilibili
   Dijkstra
   
   Prim
   

2. 【手动可视化】Algorithm Visualizer （https://algorithm-visualizer.org/）

3. 【手动可视化】Data Structure Visualizations (https://www.cs.usfca.edu/~galles/visualization/Algorithms.html)

5.1 掌握图的定义，包括完全图、连通图、简单路径、有向图、无向图、无环图等，明确理解图和二叉树、树和森林这种结构之间的异同点

图的基本定义

期末考试选择题中考察了连通分量和子图的区别。
图（Graph）是由节点（Vertex）和边（Edge）组成的一种数据结构，表示节点之间的关系。图分为有向图和无向图，边可以有权重。若图的顶点数为n，则它得生成树含有n-1条边。

1. 节点（Vertex）： 表示图中的一个元素或实体。
2. 边（Edge）： 表示节点之间的关系，可以是有向的或无向的。
3. 度（Degree）： 图中与该点相连的边数

无向图：几条边就是几个度（全部顶点的度的和等于边数的两倍）d=2e
有向图：某顶点的度=出度数+入度数（全部顶点的度=所有顶点出度+入度）
子图：就是一个整图的一部分，但是必须子图也是图。且也就是说边和顶点需要一起出现。

图的分类

1. 有向图（Directed Graph）： 边有方向，从一个节点指向另一个节点。
2. 无向图（Undirected Graph）： 边没有方向，两个节点之间的关系是双向的。
3. 加权图（Weighted Graph）： 边带有权重，表示节点之间的距离或成本。
4. 无权图（Unweighted Graph）： 边没有权重，只表示节点之间的连接关系。
5. 完全图（Complete Graph）： 每一对节点之间都有一条边。

图的连通性

1. 连通图（Connected Graph）： 任意两个节点之间都存在路径，即图中没有孤立的节点。
2. 非连通图（Disconnected Graph）： 存在孤立的节点，有些节点之间没有路径。

图的路径和环

1. 路径（Path）： 由边连接的一系列节点，形成的序列称为路径。
2. 简单路径（Simple Path）： 不经过重复节点的路径。
3. 环（Cycle）： 起点和终点相同的路径。

图与树、森林的异同

1. 相同点： 图、树和森林都是由节点和边构成的数据结构，表示元素之间的关系。
2. 不同点：
   • 图 vs 树： 树是一种特殊的无环图，所有节点通过唯一的路径相互连接，并且没有孤立的节点。
   • 图 vs 森林： 森林是多棵树的集合，每棵树都是独立的。

5.2 掌握图采用邻接矩阵和邻接表进行存储的差异性

图可以使用邻接矩阵和邻接表两种方式进行存储，它们各有优缺点，适用于不同的场景。
期末考试有考到把给出的无向图的邻接矩阵写出来

邻接矩阵

邻接矩阵是使用二维数组来表示图的连接关系。对于有向图，矩阵中的元素 a[i][j] 表示从节点 i 到节点 j 是否存在边；对于无向图，矩阵是对称的，a[i][j] = a[j][i]。

优点：

1. 查找边的存在性快速： 直接访问矩阵元素即可确定两个节点之间是否有边。
2. 适用于稠密图： 当图边比较多时，矩阵存储相对紧凑。

缺点：

1. 浪费空间： 对于稀疏图，大部分元素为 0，会占用大量空间。
2. 添加或删除节点麻烦： 需要调整整个矩阵的大小。

邻接表

邻接表是通过链表来表示图的连接关系。对于每个节点，用一个链表存储与它相邻的节点。

优点：

1. 节省空间： 对于稀疏图，只存储存在边的部分，节省空间。
2. 添加或删除节点方便： 通过调整链表，添加或删除节点相对方便。

缺点：

1. 查找边的存在性相对慢： 需要遍历链表来确定两个节点之间是否有边。
2. 适用于稀疏图： 对于密集图，可能会占用更多的空间。

比较

1. 空间复杂度： 邻接矩阵通常占用更多的空间，而邻接表对于稀疏图更经济。
2. 时间复杂度： 邻接矩阵在查找边的存在性上更快，而邻接表在添加或删除节点上更快。
3. 适用场景： 邻接矩阵适用于稠密图，而邻接表适用于稀疏图。

Java 代码示例

1.邻接矩阵

class GraphMatrix {
    private int[][] matrix;

    public GraphMatrix(int n) {
        matrix = new int[n][n];
    }

    public void addEdge(int i, int j) {
        matrix[i][j] = 1;
        matrix[j][i] = 1; // 对于无向图，设置对称位置的元素
    }

    // 其他操作...
}

2.邻接表

import java.util.LinkedList;

class GraphList {
    private int V;
    private LinkedList<Integer>[] adjList;

    public GraphList(int V) {
        this.V = V;
        adjList = new LinkedList[V];
        for (int i = 0; i < V; ++i) {
            adjList[i] = new LinkedList<>();
        }
    }

    public void addEdge(int i, int j) {
        adjList[i].add(j);
        adjList[j].add(i); // 对于无向图，添加到两个节点的邻接表中
    }

    // 其他操作...
}

5.3 掌握广度优先遍历和深度优先遍历

广度优先遍历（BFS）

广度优先遍历是一种逐层访问图中节点的遍历方法。从起始节点开始，依次访问其所有相邻节点，然后再逐层访问下一层的节点。

算法步骤

1. 将起始节点放入队列。
2. 从队列中弹出一个节点，访问该节点并将其所有未访问的相邻节点加入队列。
3. 重复步骤 2，直到队列为空。

Java 代码示例

import java.util.LinkedList;
import java.util.Queue;

class Graph {
    private int V; // 节点数量
    private LinkedList<Integer>[] adjList;

    public Graph(int V) {
        this.V = V;
        adjList = new LinkedList[V];
        for (int i = 0; i < V; ++i) {
            adjList[i] = new LinkedList<>();
        }
    }

    public void addEdge(int i, int j) {
        adjList[i].add(j);
        adjList[j].add(i); // 对于无向图，添加到两个节点的邻接表中
    }

    public void bfs(int start) {
        boolean[] visited = new boolean[V];
        Queue<Integer> queue = new LinkedList<>();
        visited[start] = true;
        queue.offer(start);

        while (!queue.isEmpty()) {
            int current = queue.poll();
            System.out.print(current + " ");

            for (int neighbor : adjList[current]) {
                if (!visited[neighbor]) {
                    visited[neighbor] = true;
                    queue.offer(neighbor);
                }
            }
        }
    }
}

深度优先遍历（DFS）

深度优先遍历是一种递归或栈的方式遍历图的方法。从起始节点开始，访问一个相邻节点，然后递归或压栈访问该节点的未访问相邻节点，直到没有未访问的相邻节点为止，然后回溯到上一层继续。

算法步骤

1. 从起始节点开始递归或使用栈，访问该节点并标记为已访问。
2. 对该节点的未访问相邻节点，递归或压栈访问它们。
3. 重复步骤 2，直到当前路径上没有未访问的相邻节点。
4. 回溯到上一层，继续步骤 2。

Java 代码示例

import java.util.LinkedList;
import java.util.Stack;

class Graph {
    private int V; // 节点数量
    private LinkedList<Integer>[] adjList;

    public Graph(int V) {
        this.V = V;
        adjList = new LinkedList[V];
        for (int i = 0; i < V; ++i) {
            adjList[i] = new LinkedList<>();
        }
    }

    public void addEdge(int i, int j) {
        adjList[i].add(j);
        adjList[j].add(i); // 对于无向图，添加到两个节点的邻接表中
    }

    public void dfs(int start) {
        boolean[] visited = new boolean[V];
        dfsRecursive(start, visited);
    }

    private void dfsRecursive(int current, boolean[] visited) {
        visited[current] = true;
        System.out.print(current + " ");

        for (int neighbor : adjList[current]) {
            if (!visited[neighbor]) {
                dfsRecursive(neighbor, visited);
            }
        }
    }
}

5.4 掌握最小生成树（Prim算法、Kruskal算法）、最短路径（Dijkstra算法）、拓扑排序的实现过程

期末考试中，选择题考察了拓扑排序（哪种算法能判断一个图中有没有环），大题中考察了Dijkstra算法（给了有向图写出最短路径，需有过程）

最小生成树

最小生成树（Minimum Spanning Tree，简称 MST）是一个连通图的生成树，其中包含了图中所有的顶点，但是只包含足够的边以使得生成树的总权重最小。两个经典的算法用于找到最小生成树：Prim 算法和 Kruskal 算法。Prim 算法更注重顶点的选择，而 Kruskal 算法更注重边的选择。
动态演示在GreedAlgorithm-prim,kruskal,dijkstra

1. Prim 算法

Prim 算法通过逐步选择连接两棵独立树的最小权重边来构建最小生成树。它始终在当前已选取的顶点集合和未选取的顶点集合之间找到权重最小的边。
注：在 Prim 算法中，通常规定图的边的权值不能为0。这是因为 Prim 算法的核心思想是选择具有最小权值的边，然后逐步构建最小生成树。如果存在权值为0的边，它们可能在选择过程中引起混淆。

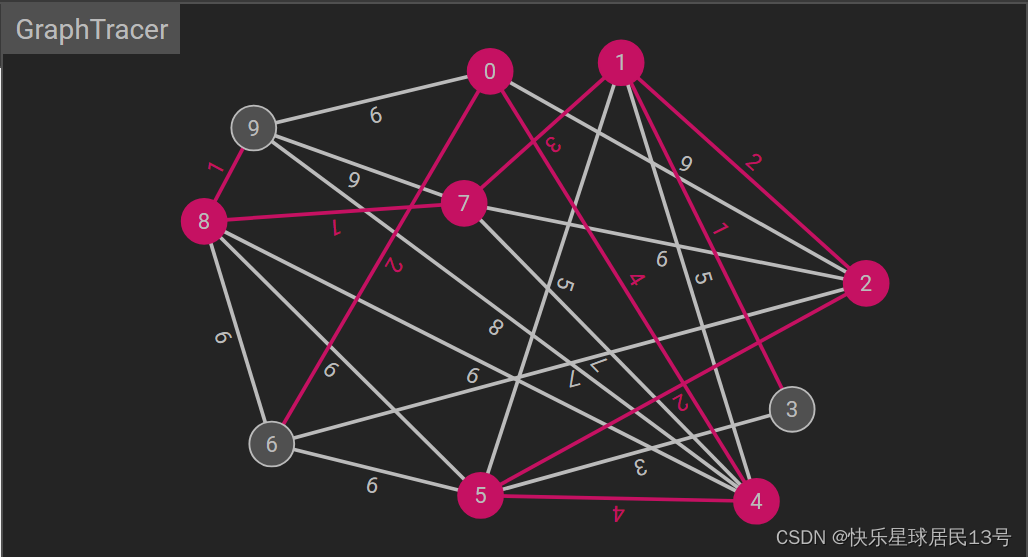
Java 代码示例

import java.util.Arrays;

class PrimAlgorithm {
    static final int V = 5;

    int minKey(int key[], boolean mstSet[]) {
        int min = Integer.MAX_VALUE, minIndex = -1;

        for (int v = 0; v < V; v++) {
            if (!mstSet[v] && key[v] < min) {
                min = key[v];
                minIndex = v;
            }
        }

        return minIndex;
    }

    void primMST(int graph[][]) {
        int parent[] = new int[V];
        int key[] = new int[V];
        boolean mstSet[] = new boolean[V];

        Arrays.fill(key, Integer.MAX_VALUE);
        key[0] = 0;
        parent[0] = -1;

        for (int count = 0; count < V - 1; count++) {
            int u = minKey(key, mstSet);
            mstSet[u] = true;

            for (int v = 0; v < V; v++) {
                if (graph[u][v] != 0 && !mstSet[v] && graph[u][v] < key[v]) {
                    parent[v] = u;
                    key[v] = graph[u][v];
                }
            }
        }

        printMST(parent, graph);
    }

    void printMST(int parent[], int graph[][]) {
        System.out.println("Edge \tWeight");
        for (int i = 1; i < V; i++) {
            System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);
        }
    }

    public static void main(String[] args) {
        PrimAlgorithm t = new PrimAlgorithm();
        int graph[][] = new int[][]{{0, 2, 0, 6, 0},
                                    {2, 0, 3, 8, 5},
                                    {0, 3, 0, 0, 7},
                                    {6, 8, 0, 0, 9},
                                    {0, 5, 7, 9, 0}};

        t.primMST(graph);
    }
}

2. Kruskal 算法

Kruskal 算法通过按权重递增的顺序选择边来构建最小生成树。它始终选择不形成环路的边，直到构建完整的最小生成树。

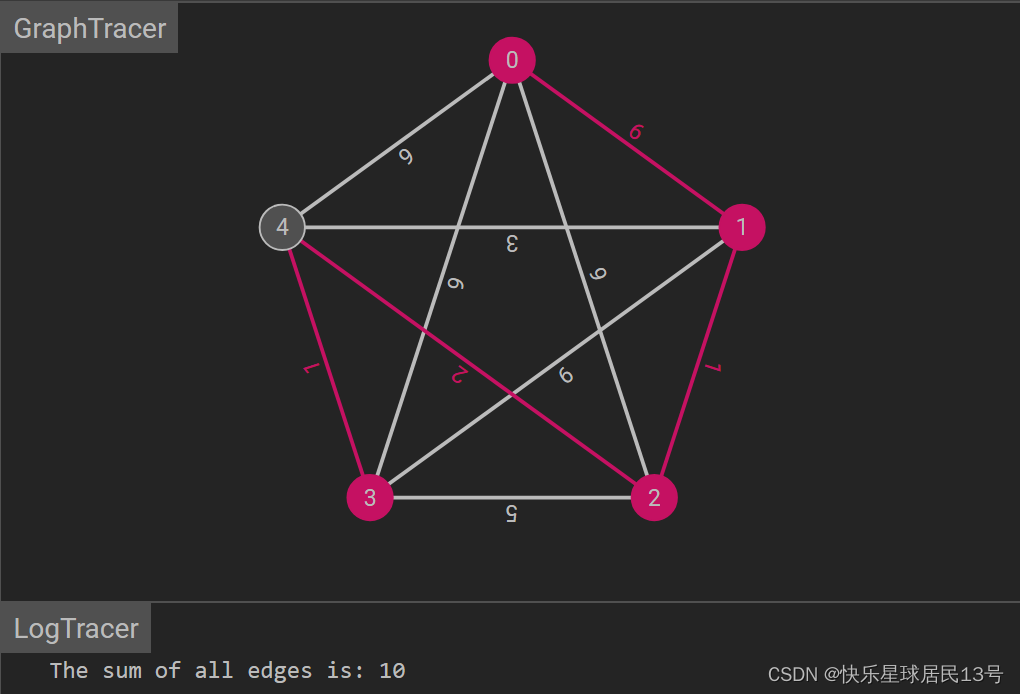
Java 代码示例：

import java.util.Arrays;

class KruskalAlgorithm {
    class Edge implements Comparable<Edge> {
        int src, dest, weight;

        public int compareTo(Edge compareEdge) {
            return this.weight - compareEdge.weight;
        }
    }

    int V, E;
    Edge edge[];

    KruskalAlgorithm(int v, int e) {
        V = v;
        E = e;
        edge = new Edge[E];
        for (int i = 0; i < e; ++i)
            edge[i] = new Edge();
    }

    int find(int parent[], int i) {
        if (parent[i] == -1)
            return i;
        return find(parent, parent[i]);
    }

    void union(int parent[], int x, int y) {
        int xset = find(parent, x);
        int yset = find(parent, y);
        parent[xset] = yset;
    }

    void kruskalMST() {
        Edge result[] = new Edge[V];
        int e = 0;
        int i = 0;
        for (i = 0; i < V; ++i)
            result[i] = new Edge();

        Arrays.sort(edge);

        int parent[] = new int[V];
        Arrays.fill(parent, -1);

        i = 0;

        while (e < V - 1) {
            Edge nextEdge = edge[i++];
            int x = find(parent, nextEdge.src);
            int y = find(parent, nextEdge.dest);

            if (x != y) {
                result[e++] = nextEdge;
                union(parent, x, y);
            }
        }

        System.out.println("Edge \tWeight");
        for (i = 0; i < e; ++i)
            System.out.println(result[i].src + " - " + result[i].dest + "\t" + result[i].weight);
    }

    public static void main(String[] args) {
        int V = 4;
        int E = 5;
        KruskalAlgorithm graph = new KruskalAlgorithm(V, E);

        graph.edge[0].src = 0;
        graph.edge[0].dest = 1;
        graph.edge[0].weight = 10;

        graph.edge[1].src = 0;
        graph.edge[1].dest = 2;
        graph.edge[1].weight = 6;

        graph.edge[2].src = 0;
        graph.edge[2].dest = 3;
        graph.edge[2].weight = 5;

        graph.edge[3].src = 1;
        graph.edge[3].dest = 3;
        graph.edge[3].weight = 15;

        graph.edge[4].src = 2;
        graph.edge[4].dest = 3;
        graph.edge[4].weight = 4;

        graph.kruskalMST();
    }
}

最短路径

Dijkstra 算法

Dijkstra 算法用于找到图中单源最短路径。它从起始节点开始，逐步选择距离最近的节点，并更新到其他节点的最短距离。

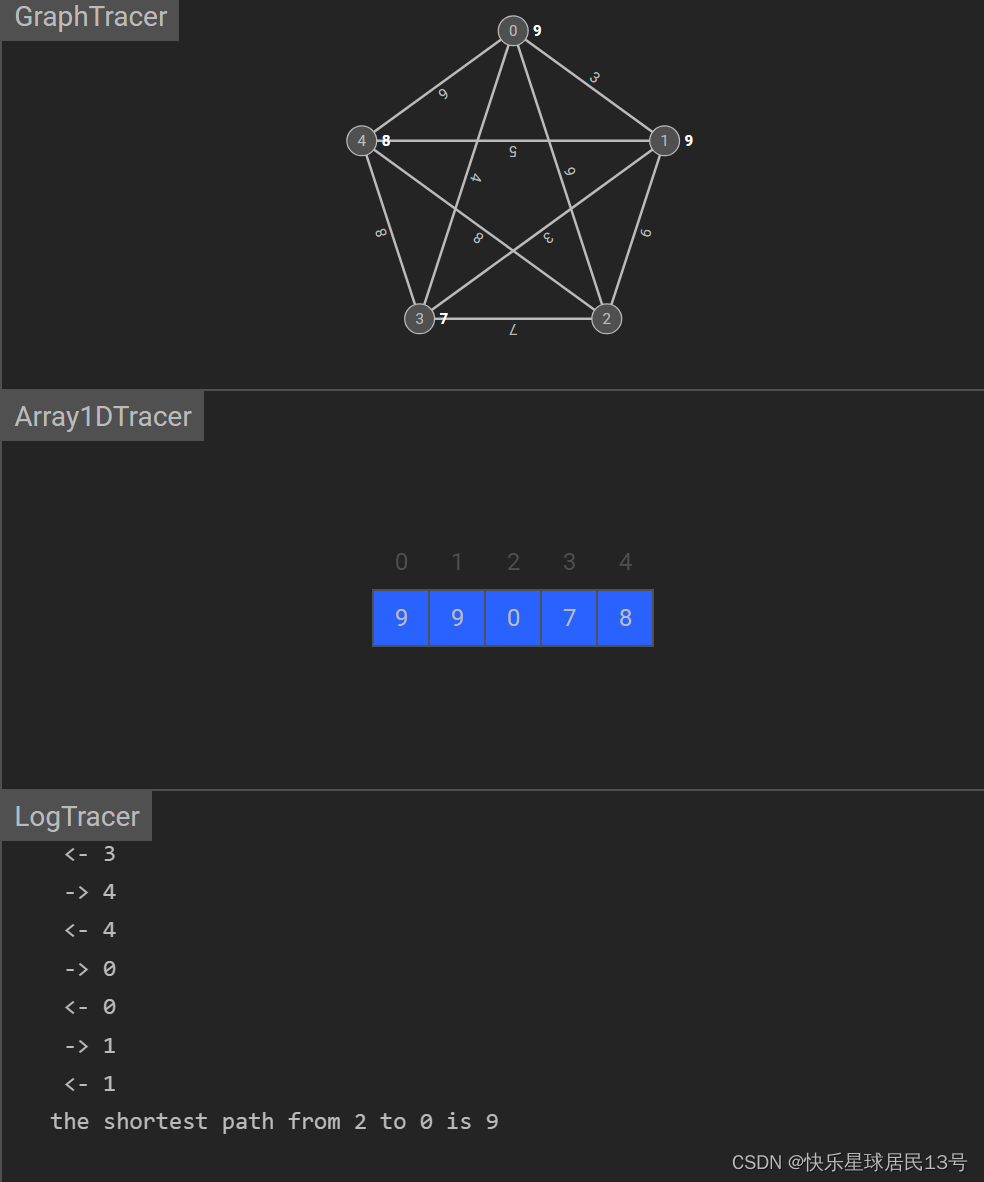
Java 代码示例

import java.util.Arrays;

class DijkstraAlgorithm {
    static final int V = 9;

    int minDistance(int dist[], boolean sptSet[]) {
        int min = Integer.MAX_VALUE, min_index = -1;

        for (int v = 0; v < V; v++) {
            if (!sptSet[v] && dist[v] <= min) {
                min = dist[v];
                min_index = v;
            }
        }

        return min_index;
    }

    void printSolution(int dist[]) {
        System.out.println("Vertex \tDistance from Source");
        for (int i = 0;

 i < V; i++)
            System.out.println(i + " \t" + dist[i]);
    }

    void dijkstra(int graph[][], int src) {
        int dist[] = new int[V];
        boolean sptSet[] = new boolean[V];

        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[src] = 0;

        for (int count = 0; count < V - 1; count++) {
            int u = minDistance(dist, sptSet);
            sptSet[u] = true;

            for (int v = 0; v < V; v++) {
                if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE &&
                        dist[u] + graph[u][v] < dist[v]) {
                    dist[v] = dist[u] + graph[u][v];
                }
            }
        }

        printSolution(dist);
    }

    public static void main(String[] args) {
        int graph[][] = new int[][]{{0, 4, 0, 0, 0, 0, 0, 8, 0},
                                    {4, 0, 8, 0, 0, 0, 0, 11, 0},
                                    {0, 8, 0, 7, 0, 4, 0, 0, 2},
                                    {0, 0, 7, 0, 9, 14, 0, 0, 0},
                                    {0, 0, 0, 9, 0, 10, 0, 0, 0},
                                    {0, 0, 4, 14, 10, 0, 2, 0, 0},
                                    {0, 0, 0, 0, 0, 2, 0, 1, 6},
                                    {8, 11, 0, 0, 0, 0, 1, 0, 7},
                                    {0, 0, 2, 0, 0, 0, 6, 7, 0}};

        DijkstraAlgorithm t = new DijkstraAlgorithm();
        t.dijkstra(graph, 0);
    }
}

拓扑排序

拓扑排序用于有向无环图（DAG），它确定图中节点的线性顺序，使得对于每一条有向边 (u, v)，节点 u 在拓扑排序中都出现在节点 v 的前面。

Java 代码示例

import java.util.*;

class TopologicalSort {
    private int V;
    private LinkedList<Integer> adj[];

    TopologicalSort(int v) {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    void addEdge(int v, int w) {
        adj[v].add(w);
    }

    void topologicalSortUtil(int v, boolean visited[], Stack<Integer> stack) {
        visited[v] = true;
        Integer i;

        Iterator<Integer> it = adj[v].iterator();
        while (it.hasNext()) {
            i = it.next();
            if (!visited[i])
                topologicalSortUtil(i, visited, stack);
        }

        stack.push(v);
    }

    void topologicalSort() {
        Stack<Integer> stack = new Stack<>();

        boolean visited[] = new boolean[V];
        for (int i = 0; i < V; i++)
            visited[i] = false;

        for (int i = 0; i < V; i++)
            if (!visited[i])
                topologicalSortUtil(i, visited, stack);

        System.out.println("Topological Sort:");
        while (!stack.empty())
            System.out.print(stack.pop() + " ");
    }

    public static void main(String args[]) {
        TopologicalSort g = new TopologicalSort(6);
        g.addEdge(5, 2);
        g.addEdge(5, 0);
        g.addEdge(4, 0);
        g.addEdge(4, 1);
        g.addEdge(2, 3);
        g.addEdge(3, 1);

        g.topologicalSort();
    }
}