堆与二叉树(下)
接着上次的,这里主要介绍的是堆排序,二叉树的遍历,以及之前讲题时答应过的简单二叉树问题求解
堆排序
给一组数据,升序(降序)排列
思路
思考:如果排列升序,我们应该建什么堆?
首先,如果排升序,数列最后一个数是 最大数,我们的思路是通过 向上调整 或者 向下调整,数组存放的第一个数不是最小值(小堆)就是最大值(大堆),此时我们将最后一个数与第一个数交换,使得最大值放在最后,此时再使用向上调整 或者 向下调整,得到第二大的数,重复上述动作,很明显,我们需要的第一个数是最大值,因此我们需要建大堆
反之,排降序,建立小堆
代码
#include<stdio.h> void downAdjust(int* pa, int parent, int n) { int child = parent * 2 + 1; while (child < n) { if (child + 1 < n && pa[child] > pa[child + 1]) { child++; } if (pa[parent] > pa[child]) { swap(&pa[parent], &pa[child]); } else { break; } parent = child; child = parent * 2 + 1; } } int main() { int arr[] = { 1,3,2,5,7,4,7,4,2,5,6,8}; int n = sizeof(arr) / sizeof(arr[0]); for (int i = (n - 1 - 1) / 2; i >= 0; i--) { downAdjust(arr, i, n); } for (int i = n; i > 0; ) { swap(&arr[0], &arr[i - 1]); downAdjust(arr, 0, --i); } for (int i = 0; i < n; i++) { printf("%d ", arr[i]); } return 0; }
topK算法
在一组数据中,选出k个最大(最小)的数
思路
如果我们选择k个最大的数,假设数组的前k个数就是最大的数,这 k个数建立 小堆,带一个数与 后面的从第 k + 1个数开始,进行比较,如果比第一个数的就换下来,然后向下调整,直到每个所有数都比较完了
代码
void downAdjust(int* pa, int parent, int n) { int child = parent * 2 + 1; while (child < n) { if (child + 1 < n && pa[child] > pa[child + 1]) { child++; } if (pa[parent] > pa[child]) { swap(&pa[parent], &pa[child]); } else { break; } parent = child; child = parent * 2 + 1; } } #include<stdio.h> int main() { int arr[] = { 1,6,10,3,5,8,46,23,6,25,3,40 }; int n = sizeof(arr) / sizeof(arr[0]); int k = 0; scanf("%d", &k); for (int i = (k - 1 - 1) / 2; i >= 0; i--) { downAdjust(arr, i, n); } for (int i = k; i < n; i++) { if (arr[i] > arr[0]) { swap(&arr[i], &arr[0]); downAdjust(arr, 0, k); } } for (int i = 0; i < k; i++) { printf("%d ", arr[i]); } return 0; }
五. 二叉树的实现
1. 链接结构搭建二叉树
代码
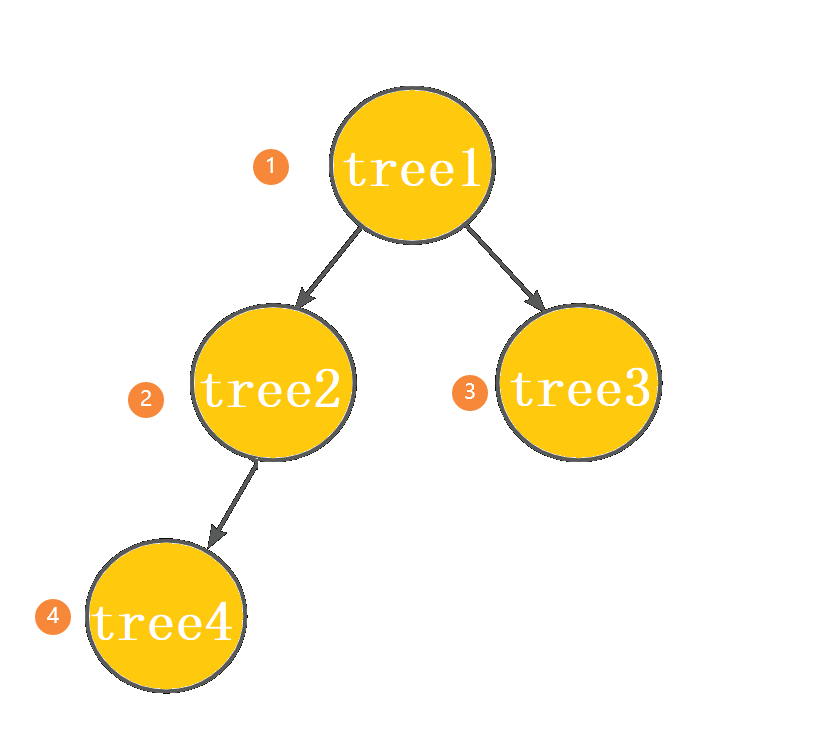
typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL *creatnode(TLType x) { TL*pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL *tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(3); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; return tree1; } #include<stdio.h> int main() { TL* p = NULL; p = CreatTree(); }我们搭建了一个这样的树结构:
2. 二叉树的遍历
二叉树的遍历可以分三种:前序,中序,后序,层序
a. 前序遍历:(根,左子树,右子树)
举例
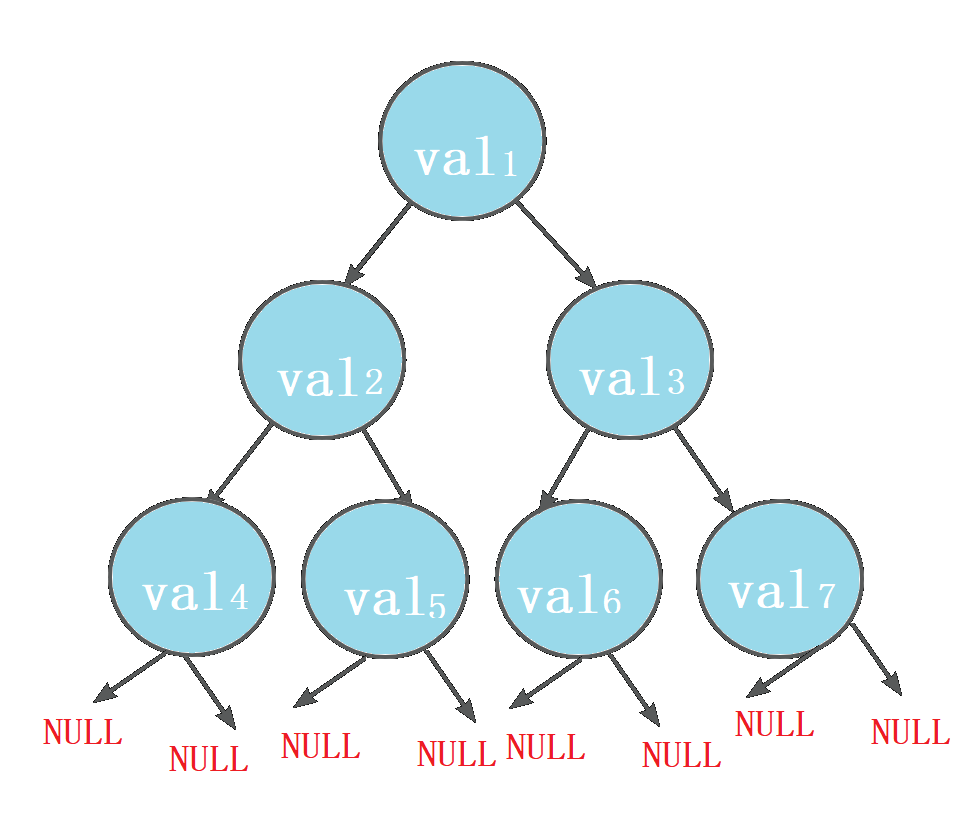
这棵树的前序遍历是怎样的?(包括空树,用N表示)
val1 val2 val4 N N val5 N N val3 val6 N N val7 N N
代码实现?
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL *creatnode(TLType x) { TL*pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL *tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; return tree1; } #include<stdio.h> void PrevOrder(TL *root) { if (root == NULL) { printf("N "); return; } printf("%d ", root->val); PrevOrder(root->left); PrevOrder(root->right); } int main() { TL* p = NULL; p = CreatTree(); PrevOrder(p); }运行结果:
b. 中序遍历:(左子树,根,右子树)
举例
这棵树的中序遍历是怎样的?(包括空树,用N表示)
N val4 N val2 N val5 N val1 N val6 N val3 N val7 N
?代码实现
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL *creatnode(TLType x) { TL*pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL *tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; return tree1; } #include<stdio.h> void InOder(TL* root) { if (root == NULL) { printf("N "); return; } InOder(root->left); printf("%d ", root->val); InOder(root->right); } int main() { TL* p = NULL; p = CreatTree(); InOder(p); }运行结果:
c. 后序遍历:(左子树,右子树,根)
举例
这棵树的后序遍历是怎样的?(包括空树,用N表示)
N N val4 N N val5 val2 N N val6 N N val7 val3 val1
代码实现?
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; return tree1; } void PostOder(TL* root) { if (root == NULL) { printf("N "); return; } PostOder(root->left); PostOder(root->right); printf("%d ", root->val); } int main() { TL* p = NULL; p = CreatTree(); PostOder(p); }运行结果:
d. 层序遍历
一排排的遍历
画图举例
实现思路?
这里我们借助队列(可以先进先出),开辟的数组里面存放根节点的地址(通过地址可以找到左右子树,否则如果存值是没有办法找到左右子树),打印完根节点的值,就释放,存入左右子树的节点
代码实现
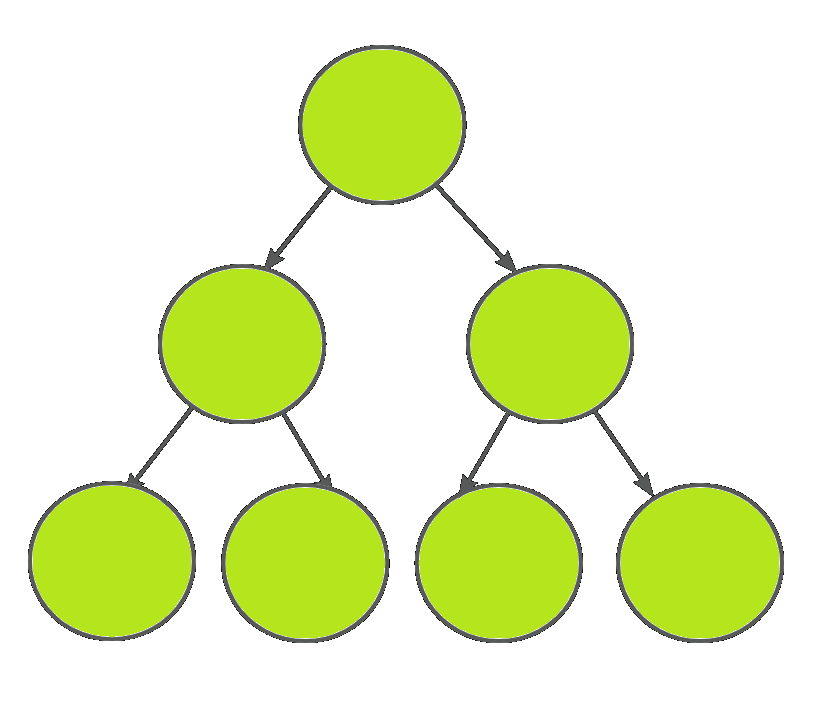
实现的二叉树是这样的:
#include<stdio.h> #include<stdlib.h> #include<assert.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; return tree1; } typedef struct QueueNode { struct QueueNode* next; TL* data; }QNode; typedef struct Queue { QNode* head; QNode* tail; int size; }Que; void QueueInit(Que* pq) { assert(pq); pq->head = pq->tail = NULL; pq->size = 0; } void QueueDestroy(Que* pq) { assert(pq); QNode* cur = pq->head; while (cur) { QNode* next = cur->next; free(cur); cur = next; } pq->head = pq->tail = NULL; pq->size = 0; } void QueuePush(Que* pq, TL* x) { assert(pq); QNode* newnode = (QNode*)malloc(sizeof(QNode)); if (newnode == NULL) { perror("malloc fail"); exit(-1); } newnode->data = x; newnode->next = NULL; if (pq->tail == NULL) { pq->head = pq->tail = newnode; } else { pq->tail->next = newnode; pq->tail = newnode; } pq->size++; } bool QueueEmpty(Que* pq) { assert(pq); return pq->head == NULL; } void QueuePop(Que* pq) { assert(pq); assert(!QueueEmpty(pq)); if (pq->head->next == NULL) { free(pq->head); pq->head = pq->tail = NULL; } else { QNode* next = pq->head->next; free(pq->head); pq->head = next; } pq->size--; } TL* QueueFront(Que* pq) { assert(pq); assert(!QueueEmpty(pq)); return pq->head->data; } int QueueSize(Que* pq) { assert(pq); return pq->size; } void leverOrder(TL* root, Que* pq) { QueuePush(pq, root); while (!QueueEmpty(pq)) { TL* pa = QueueFront(pq); printf("%d ", pa->val); QueuePop(pq); if (pa->left != NULL) { QueuePush(pq, pa->left); } if (pa->right != NULL) { QueuePush(pq, pa->right); } } } int main() { TL* p = NULL; p = CreatTree(); Que q; QueueInit(&q); leverOrder(p, &q); return 0; }运行结果:
3. 简单二叉树经典问题求解
a. 求二叉树的节点个数
思路
想要求二叉树的节点可以分成 根节点 + 左子树 + 右子树
这里的遍历类似 前序遍历
代码
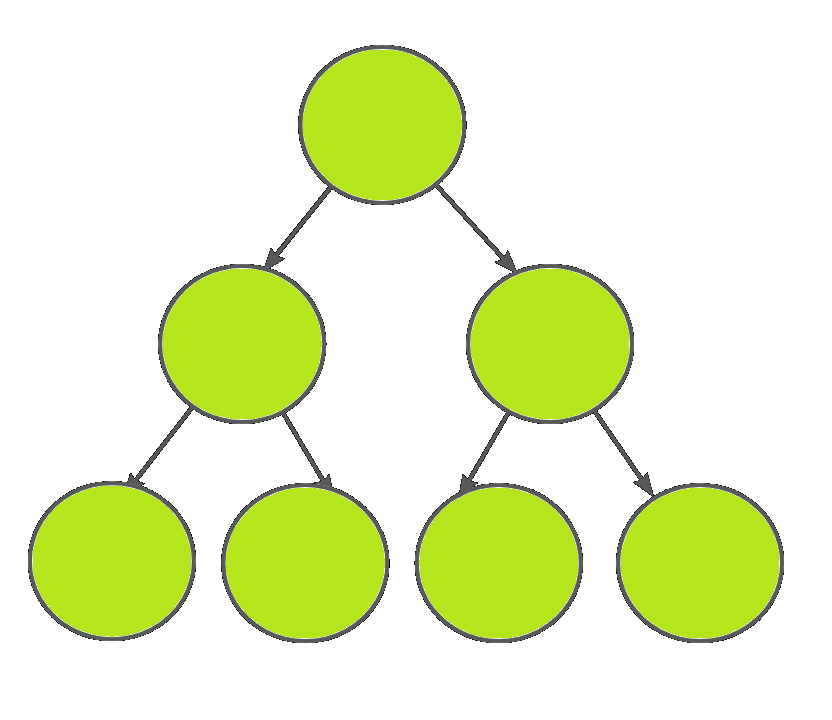
实现的树是这样的:
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; return tree1; } int TreeSize(TL* root) { if (root == NULL) { return 0; } return 1 + TreeSize(root->left) + TreeSize(root->right); } int main() { TL* p = NULL; p = CreatTree(); int size = TreeSize(p); printf("%d ", size); return 0; }
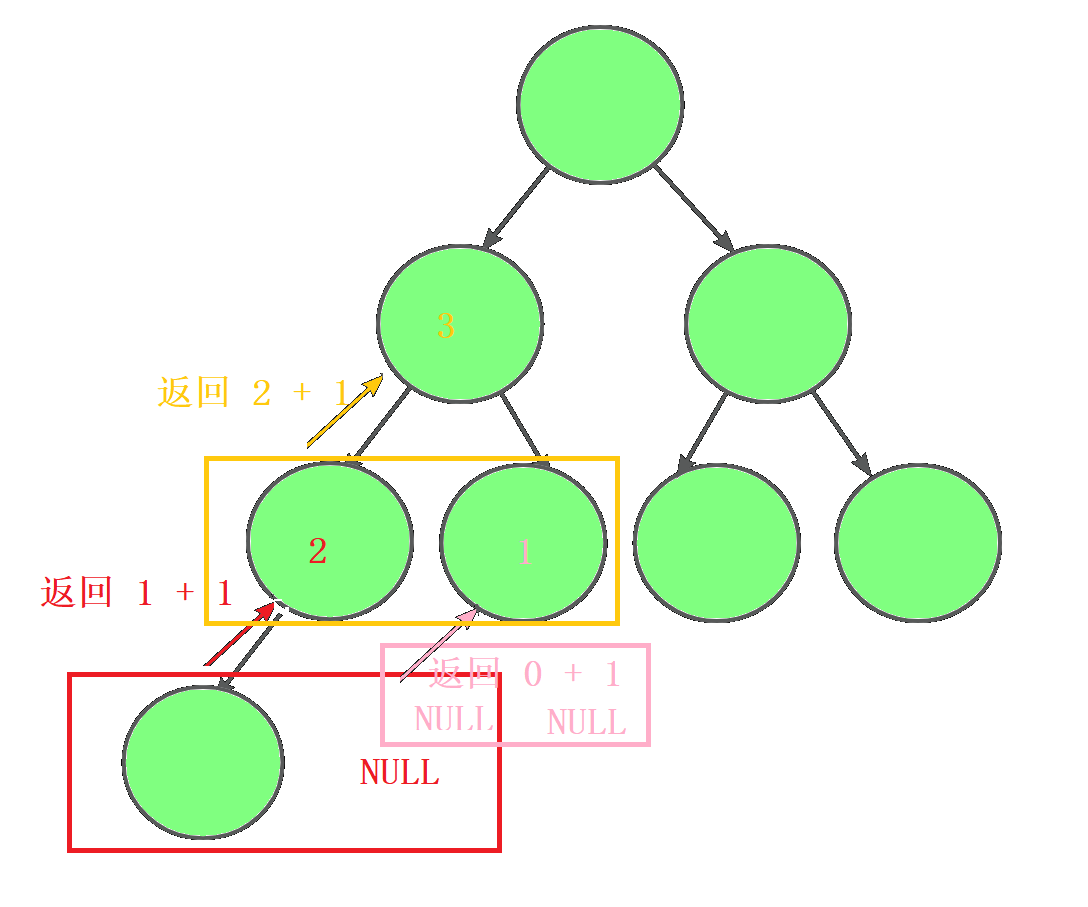
b. 求树的高度
思路
求二叉树的高度,我们需要找到到那个最长的路径,这里采用分治的思想,如果为空树,返回 0 (空树高度为 0),调用左子树和右子树都会 + 1(+ 1可以理解成加上节点的高度),对比左子树和右子树,返回高度最大的那个
注:每求一次左右节点个数时,一定要保存,否则会有很大的时间浪费
代码
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); TL* tree8 = creatnode(8); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; tree4->left = tree8; return tree1; } int TreeHigh(TL* root) { if (root == NULL) { return 0; } int Left = 1 + TreeHigh(root->left); int Right = 1 + TreeHigh(root->right) ; return Left > Right ? Left : Right; } int main() { TL* p = NULL; p = CreatTree(); int high = TreeHigh(p); printf("%d ", high); return 0; }
c. 求根节点的个数
思路
判断是否是根节点的方法就是判断它的左右子树是否是 空树,我们只需要遍历这棵树就行,但如果遍历时,根节点遇到空树这也是一种结束条件
代码
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); TL* tree8 = creatnode(8); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; tree4->left = tree8; return tree1; } int RootSize(TL* root) { if (root == NULL) { return 0; } if (root->left == NULL && root->right == NULL) { return 1; } return RootSize(root->left) + RootSize(root->right); } int main() { TL* p = NULL; p = CreatTree(); int root = RootSize(p); printf("%d ", root); return 0; }
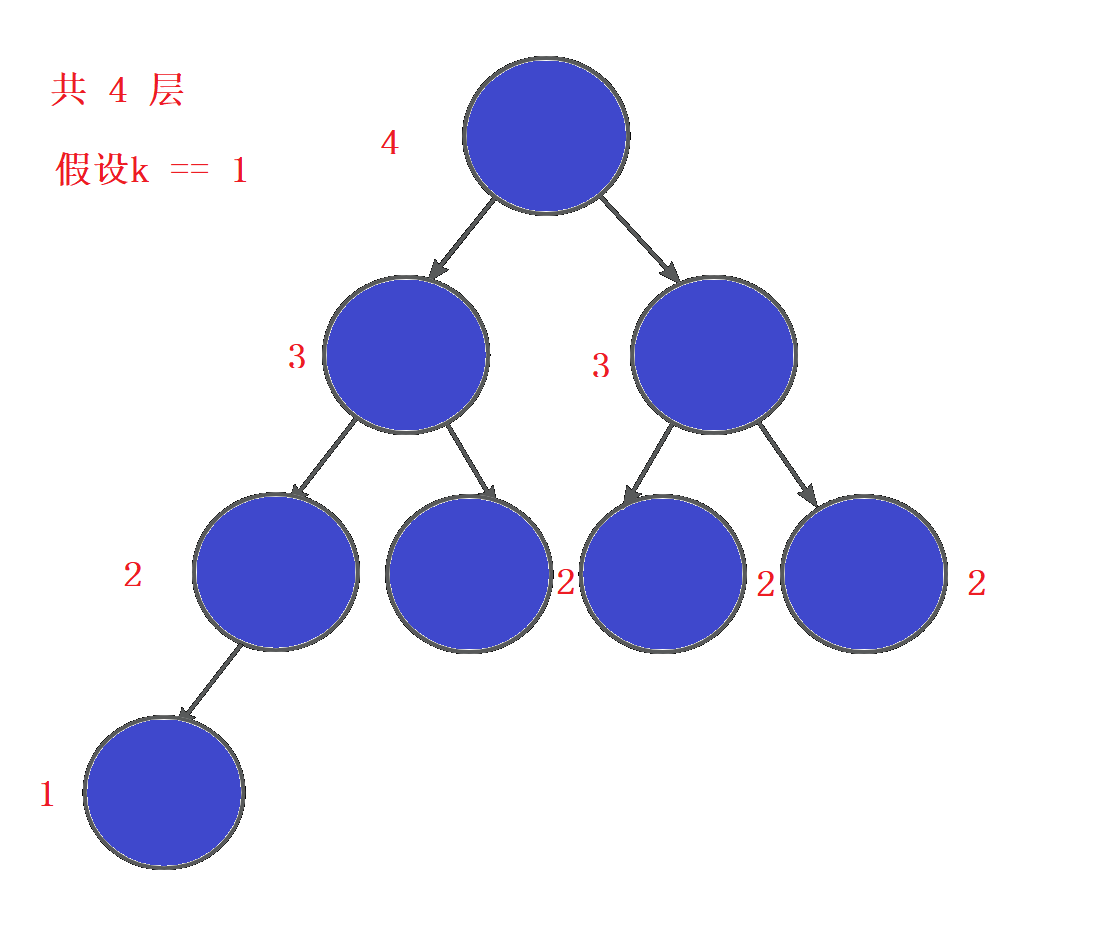
d. 求倒数第k排节点的个数
思路
这个可以是求树的高度的变形,将计数倒过来
代码?
#include<stdio.h> #include<stdlib.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); TL* tree8 = creatnode(8); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; tree4->left = tree8; return tree1; } int TreeHigh(TL* root) { if (root == NULL) { return 0; } int Left = 1 + TreeHigh(root->left); int Right = 1 + TreeHigh(root->right) ; return Left > Right ? Left : Right; } int RootKsize(TL* root,int n,int k) { if (root == NULL) { return 0; } if (n == k) { return 1; } return RootKsize(root->left, n - 1, k) + RootKsize(root->right, n - 1, k); } int main() { int k = 0; scanf("%d", &k); TL* p = NULL; p = CreatTree(); int high = TreeHigh(p); int rootk = RootKsize(p, high, k); printf("%d ", rootk); return 0; }
e. 判断是否是相同的树
思路
采用前序,先比较根节点是否相同,再比较左右子树是否相同
代码
#include<stdio.h> #include<stdlib.h> #include<stdbool.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree1() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); TL* tree8 = creatnode(8); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; tree4->left = tree8; return tree1; } TL* CreatTree2() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(3); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; return tree1; } bool IsSameTree(TL* root1,TL* root2) { if (root1 == NULL && root2 == NULL) { return true; } if (root1 == NULL || root2 == NULL) { return false; } if (root1->val != root2->val) { return false; } return IsSameTree(root1->left, root2->left) && IsSameTree(root1->right, root2->right); } int main() { TL* p = NULL; p = CreatTree1(); TL* q = CreatTree2(); printf("%d ", IsSameTree(p, q)); return 0; }
f. 找到某个值,返回节点的地址
思路
前序遍历完数组,如果对比左右子树,判断是否找到节点的地址
代码
#include<stdio.h> #include<stdlib.h> #include<stdbool.h> typedef int TLType; typedef struct TreeList { TLType val; struct TreeList* left; struct TreeList* right; }TL; TL* creatnode(TLType x) { TL* pa = (TL*)malloc(sizeof(TL)); if (pa == NULL) { perror("malloc"); return; } TL* newnode = pa; newnode->left = newnode->right = NULL; newnode->val = x; return newnode; } TL* CreatTree() { TL* tree1 = creatnode(1); TL* tree2 = creatnode(2); TL* tree3 = creatnode(2); TL* tree4 = creatnode(4); TL* tree5 = creatnode(5); TL* tree6 = creatnode(6); TL* tree7 = creatnode(7); TL* tree8 = creatnode(8); tree1->left = tree2; tree1->right = tree3; tree2->left = tree4; tree2->right = tree5; tree3->left = tree6; tree3->right = tree7; tree4->left = tree8; return tree1; } TL* FindRoot(TL* root,int m) { if (root == NULL) { return NULL; } if (root->val == m) { return root; } TL* Left = FindRoot(root->left, m); TL* Right = FindRoot(root->right, m); if (Left == NULL && Right == NULL) { return NULL; } if (Left == NULL && Right != NULL) { return Right; } else { return Left; } } int main() { TL* p = NULL; p = CreatTree(); int m = 0; scanf("%d", &m); TL *root = FindRoot(p,m); if (root == NULL) { printf("找不到\n"); } else { printf("%d ", root->val); } return 0; }
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Postman基本使用、测试环境(Environment)配置
- Mysql的聚簇索引(聚集索引)和非聚簇索引的区别
- 什么是双亲委派模式(有什么作用?)
- FFmpeg之HWContextType
- 【时钟】分布式时钟HLC|Logical Time|Vector Clock|True Time
- 计算机毕业设计 | SpringBoot宠物店管理系统(附源码)
- “ShadowEstimationHeight“app Tech Support(URL)
- 房产数据分析可视化:某网租房数据的探索与展示
- fastjson是什么东西,怎么用?
- Spring高手之路-SpringBean的生命周期