在数据中查找峰值

使用?findpeaks?函数求出一组数据中局部最大值的值和位置。

????????文件?spots_num?包含从 1749 年到 2012 年每年观测到的太阳黑子的平均数量。求出最大值及其出现的年份。将它们与数据一起绘制出来。

load("spots_num")

[pks,locs] = findpeaks(avSpots);

plot(year,avSpots,year(locs),pks,"o")
xlabel("Year")
ylabel("Sunspot Number")
axis tight

如图所示：

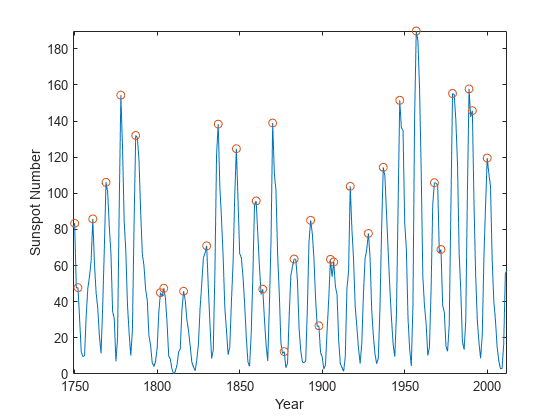
????????一些峰值彼此非常接近。有些峰值不会周期性重复出现。每 50 年大约有五个这样的峰值。

????????为了更好地估计周期持续时间，请再次使用 findpeaks，但这次将峰间间隔限制为至少六年。计算最大值之间的间隔均值。

[pks,locs] = findpeaks(avSpots,MinPeakDistance=6);

plot(year,avSpots,year(locs),pks,"o")
xlabel("Year")
ylabel("Sunspot Number")
axis tight
legend(["Data" "peaks"],Location="NorthWest")

如图所示：

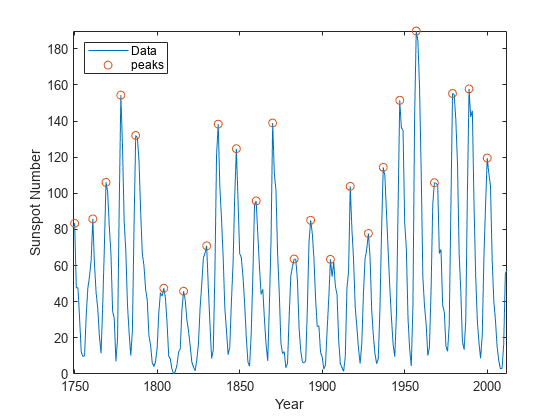
meanCycle = mean(diff(locs))
meanCycle = 10.8696

????????众所周知，太阳活动周期大约为 11 年。我们使用傅里叶变换来检验这一周期。减去信号的均值以重点关注其波动。采样率以年为单位。使用从零到奈奎斯特频率的频率。

fs = 1;
Nf = 512;

df = fs/Nf;
f = 0:df:fs/2-df;

trSpots = fftshift(fft(avSpots-mean(avSpots),Nf));
dBspots = mag2db(abs(trSpots(Nf/2+1:Nf)));

plot(f,dBspots)
xline(1/meanCycle,Color="#77AC30")
xlabel("Frequency (year^{-1})")
ylabel("| FFT | (dB)")
ylim([20 85])
text(1/meanCycle + 0.02,25,"<== 1/"+num2str(meanCycle))

如图所示：

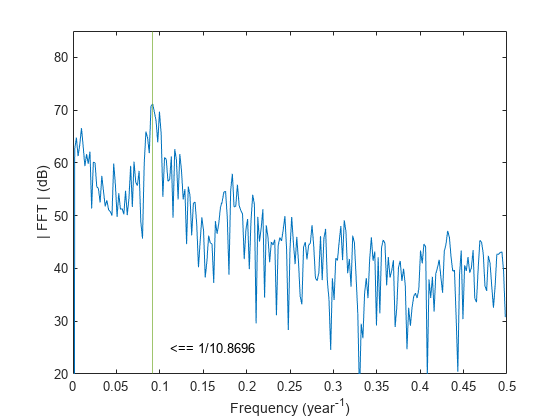
????????傅里叶变换确实在预期频率处出现峰值，证实了 11 年的估计值是准确的。还可以通过定位傅里叶变换的最高峰值来求得周期。这两个估计值非常吻合。

[pk,MaxFreq] = findpeaks(dBspots,NPeaks=1,SortStr="descend");

Period = 1/f(MaxFreq)
Period = 10.8936


hold on
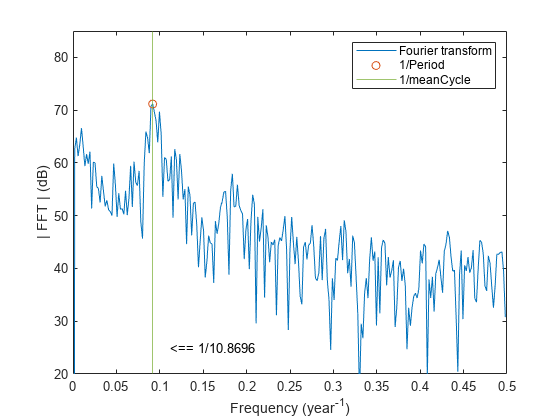
plot(f(MaxFreq),pk,"o")
hold off
legend(["Fourier transform" "1/meanCycle" "1/Period"])

如图所示：