leetcode—矩阵

1 矩阵置零

给定一个?m x n?的矩阵，如果一个元素为?0?，则将其所在行和列的所有元素都设为?0?。请使用?原地?算法。

示例 1：

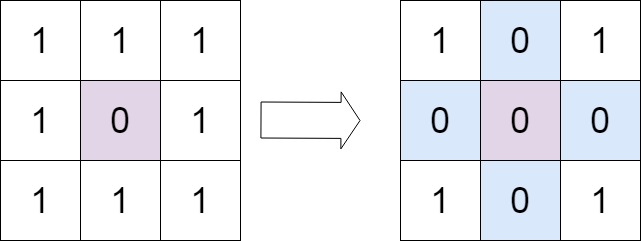
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

方法一：

使用标记数组

1. 新建两个标记数组 row column
2. 第一次遍历数组 记录数组中每一行 每一列 中的值是否为0
3. 第二次遍历数组 将数组中0所在的行和列设置为0

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;

        // 新建两个数组  记录二维数组的每一行和每一列是否为零
        boolean[] row = new boolean[m];
        boolean[] column = new boolean[n];

        // 第一次遍历二维数组 标记他的每一行 每一列是否为0
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(matrix[i][j] == 0){
                    row[i] = column[j] = true;
                }
            }
        }

        // 第二次遍历数组 将0所在的行和列设置为0
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(row[i] == true || column[j] == true){
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

2 螺旋矩阵

给你一个?m?行?n?列的矩阵?matrix?，请按照?顺时针螺旋顺序?，返回矩阵中的所有元素。

示例 1：

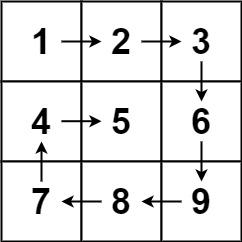
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

方法：

按层模拟，首先输出最外层的元素，其次输出次外层的元素，直到输出最内层的元素

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> order = new ArrayList<>();
        // 数组判空
        if(matrix == null || matrix.length == 0 || matrix[0].length == 0){
            return order;
        }
        int row = matrix.length;
        int column  = matrix[0].length;

        int left = 0;
        int right = column - 1;
        int top = 0;
        int bottom = row - 1;

        // 螺旋矩阵循环入口
        while(left <= right && top <= bottom){
            // 从左到右遍历上侧元素
            for(int colu = left; colu <= right; colu++){
                order.add(matrix[top][colu]);
            }
            // 从上到下遍历右侧元素
            for(int row1 = top +1; row1 <= bottom; row1++){
                order.add(matrix[row1][right]);
            }

            if(left < right && top < bottom){
                // 从右到左遍历下侧元素
                for(int colu = right -1; colu > left; colu--){
                    order.add(matrix[bottom][colu]);
                }
                // 从下到上遍历左侧元素
                for(int row2 = bottom; row2 > top; row2--){
                    order.add(matrix[row2][left]);
                }
            }
            left++;
            right--;
            top++;
            bottom--;
        }
        return order;
    }
}

3 旋转图像

给定一个?n?×?n?的二维矩阵?matrix?表示一个图像。请你将图像顺时针旋转 90 度。

你必须在?原地?旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要?使用另一个矩阵来旋转图像。

示例 1：

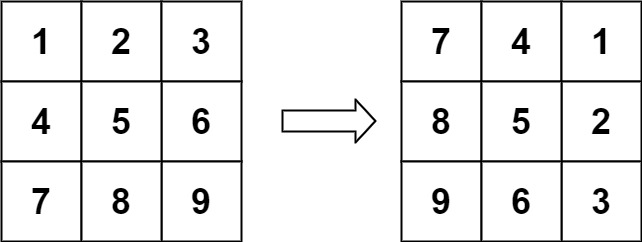
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

方法一：

借助辅助数组

?原数组中第i行第j个元素? 旋转后再数组中的位置变为? 倒数第i列第j个位置

数组下标从0开始

[row][col]? 旋转后 —> [col][n-row-1]

1. 第一次遍历数组，将数组旋转之后的值存储在辅助数组中
2. 第二次遍历数组，将辅助数组中的值赋值给原数组

class Solution {
    public void rotate(int[][] matrix) {
        // 获取数组的长度 n*n
        int n = matrix.length;
        // 新建辅助数组
        int[][] newMatrix = new int[n][n];

        // 第一次遍历数组 将旋转后的值存储在辅助数组中
        for(int row = 0; row < n; row++){
            for(int col = 0; col < n; col++){
                newMatrix[col][n - row - 1] = matrix[row][col];
            }
        }

        // 第二次遍历数组，将辅助数组中的值赋值给原数组
        for(int i = 0; i < n; i++){
            for(int j = 0; j < n; j++){
                matrix[i][j] = newMatrix[i][j];
            }
        }
    }
}

方法二：

原地旋转矩阵

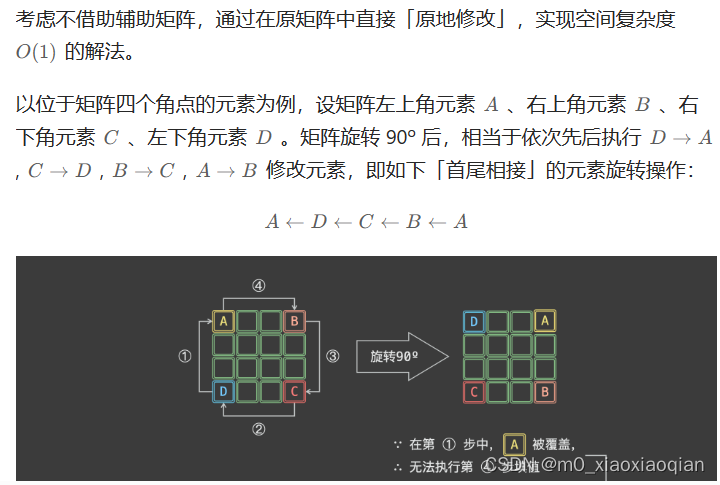
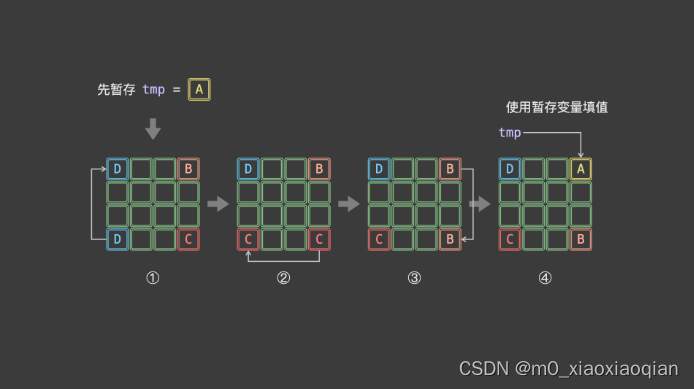
?一轮可以完成矩阵的四个元素的旋转

故：只要分别以矩阵左上角1/4的铬元素为其实点执行以上操作，即可完成矩阵旋转

• 当n为偶数时，取前n/2行，n/2列的元素为起点
• 当n为奇数时，取前n/2行，（n+1）/ 2列的元素为起点

?

class Solution {
    public void rotate(int[][] matrix) {
       // 原地旋转矩阵
       // 获取数组长度
       int n = matrix.length;

       // 旋转数组 一轮可以完成矩阵中四个元素的交换
       for(int i = 0; i < n/2; i++){
           for(int j = 0; j < (n+1)/2; j++){
               int temp = matrix[i][j];
               matrix[i][j] = matrix[n-j-1][i];
               matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
               matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
               matrix[j][n-i-1] = temp;
           }
       }
    }
}