Nas-FPN（CVPR 2019）原理与代码解析

paper：NAS-FPN: Learning Scalable Feature Pyramid Architecture for Object Detection

third-party implementation：https://github.com/open-mmlab/mmdetection/tree/main/configs/nas_fpn

本文的创新点

本文采用神经网络结构搜索（Neural Architecture Search, NAS），在一个覆盖所有跨尺度连接的新型可扩展搜索空间中发现了一个新的特征金字塔结构，NAS-FPN。与原始FPN相比，NAS-FPN显著提高了目标检测的性能，并取得了更好了速度-精度的平衡。

方法介绍

考虑到其简单而高效的结构，目标检测模型采用RetinaNet，如图2所示

作者提出了merging cell作为FPN的basic building block，将任何两层的输入特征融合为一层的输出特征。如图3所示

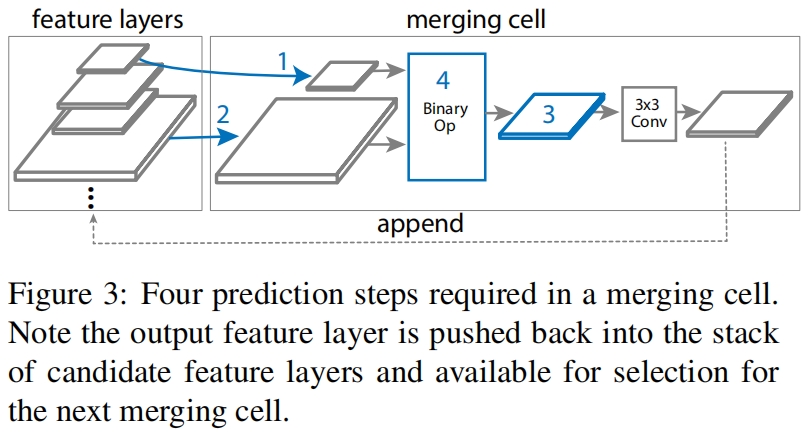
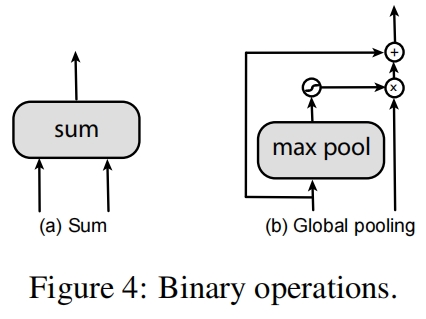
其中Binary Op包括两种候选方案，如图4所示?

最终搜索到的NAS-FPN的完整结构如图6所示?

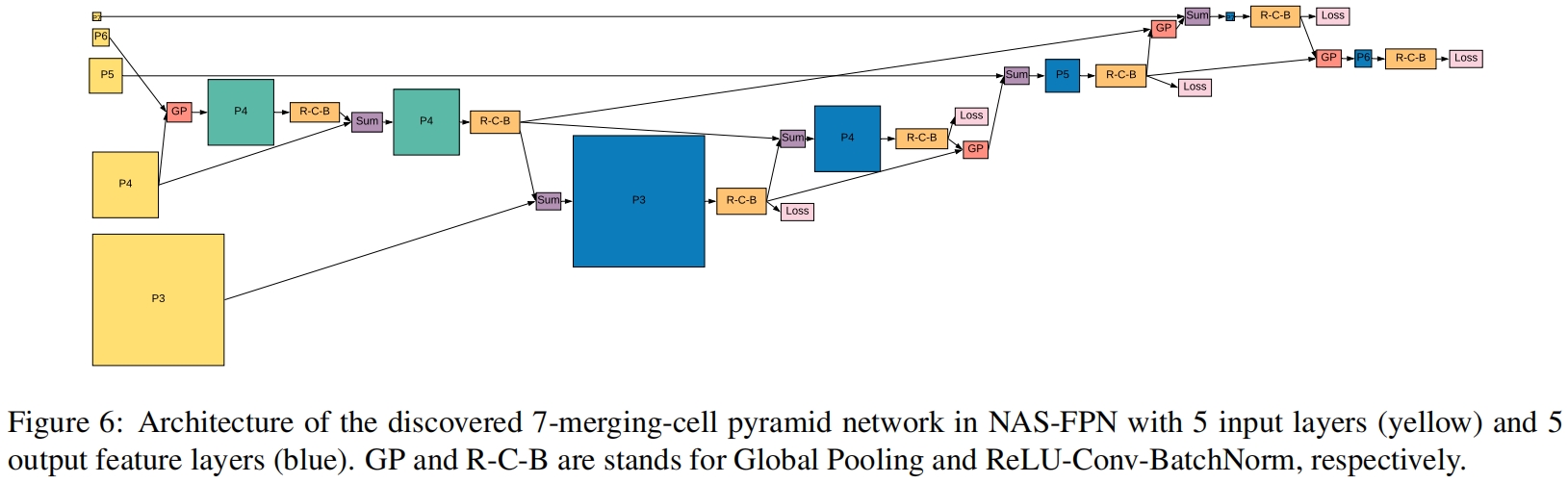
图7展示的搜索到的所有结构，其中(a)是原始FPN结构，(b)-(f)的精度逐渐变高，(f)是最终的NAS-FPN结构。

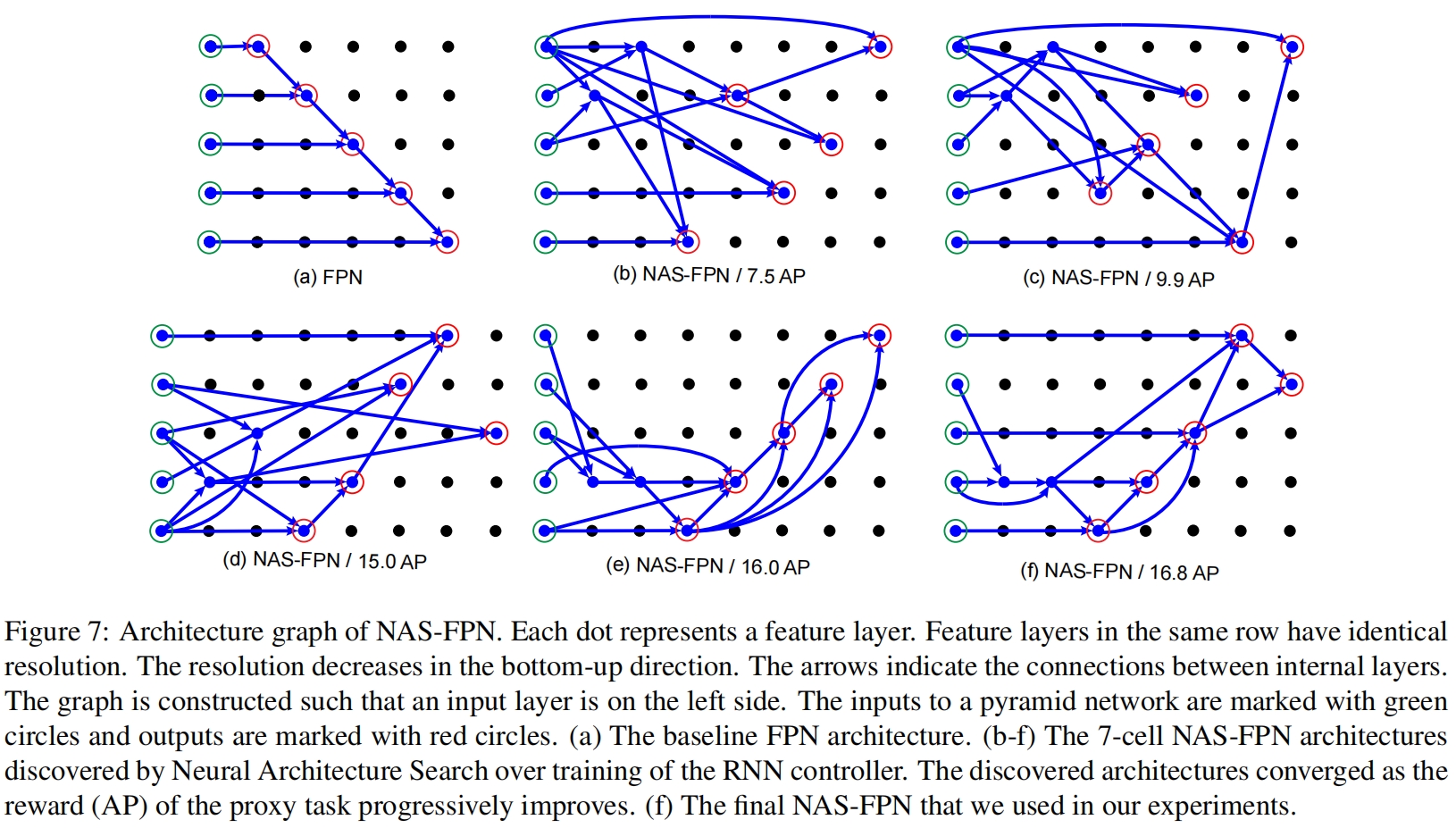
因为是搜索到的结构，并且图示非常清晰，这里就不过多介绍具体结构了。接下来结合代码和图(6)(7)的结构介绍一下实现细节?

代码解析

这里以mmdetection中的实现为例，实现代码在mmdet/models/necks/nas_fpn.py中，下面是完整的forward函数。其中self.fpn_stages=7是nas-fpn重复的次数，每个nas-fpn的输出是下一个nas-fpn的输入。forward最开始的输入是backbone的输出C2~C5，这里只取C3~C5通过lateral_conv得到P3~P5，然后进行下采样得到P6和P7，完整的P3~P7作为第一个nas-fpn的输入。

def forward(self, inputs: Tuple[Tensor]) -> tuple:
    # [(8,256,160,160),
    #  (8,512,80,80),
    #  (8,1024,40,40),
    #  (8,2048,20,20)]
    """Forward function.

     Args:
        inputs (tuple[Tensor]): Features from the upstream network, each
            is a 4D-tensor.

    Returns:
        tuple: Feature maps, each is a 4D-tensor.
    """
    # build P3-P5
    feats = [
        lateral_conv(inputs[i + self.start_level])
        for i, lateral_conv in enumerate(self.lateral_convs)
    ]  # [(8,256,80,80),(8,256,40,40),(8,256,20,20)]
    # build P6-P7 on top of P5
    for downsample in self.extra_downsamples:
        feats.append(downsample(feats[-1]))  # [..., (8,256,10,10),(8,256,5,5)]

    p3, p4, p5, p6, p7 = feats

    for stage in self.fpn_stages:
        # gp(p6, p4) -> p4_1
        # print(stage['gp_64_4'])
        p4_1 = stage['gp_64_4'](p6, p4, out_size=p4.shape[-2:])  # (8,256,40,40)
        # sum(p4_1, p4) -> p4_2
        p4_2 = stage['sum_44_4'](p4_1, p4, out_size=p4.shape[-2:])  # (8,256,40,40)
        # sum(p4_2, p3) -> p3_out
        p3 = stage['sum_43_3'](p4_2, p3, out_size=p3.shape[-2:])  # (8,256,80,80)
        # sum(p3_out, p4_2) -> p4_out
        p4 = stage['sum_34_4'](p3, p4_2, out_size=p4.shape[-2:])  # (8,256,40,40)
        # sum(p5, gp(p4_out, p3_out)) -> p5_out
        p5_tmp = stage['gp_43_5'](p4, p3, out_size=p5.shape[-2:])  # (8,256,20,20)
        p5 = stage['sum_55_5'](p5, p5_tmp, out_size=p5.shape[-2:])  # (8,256,20,20)
        # sum(p7, gp(p5_out, p4_2)) -> p7_out
        p7_tmp = stage['gp_54_7'](p5, p4_2, out_size=p7.shape[-2:])  # (8,256,5,5)
        p7 = stage['sum_77_7'](p7, p7_tmp, out_size=p7.shape[-2:])  # (8,256,5,5)
        # gp(p7_out, p5_out) -> p6_out
        p6 = stage['gp_75_6'](p7, p5, out_size=p6.shape[-2:])  # (8,256,10,10)

    return p3, p4, p5, p6, p7

在for循环中，从上到到下分别对应图6中从左到右按顺序所有的GP和Sum。其中GP对应GlobalPoolingCell，Sum对应SumCell，具体实现都在MMCV中。

GlobalPoolingCell的实现如下，其中self.input1_conv和self.input2_conv是空的，self._resize通过双线性插值进行上采样，通过max pooling进行下采样。

def forward(self,
            x1: torch.Tensor,
            x2: torch.Tensor,
            out_size: Optional[tuple] = None) -> torch.Tensor:
    assert x1.shape[:2] == x2.shape[:2]
    assert out_size is None or len(out_size) == 2
    if out_size is None:  # resize to larger one
        out_size = max(x1.size()[2:], x2.size()[2:])

    x1 = self.input1_conv(x1)
    x2 = self.input2_conv(x2)

    x1 = self._resize(x1, out_size)
    x2 = self._resize(x2, out_size)

    x = self._binary_op(x1, x2)
    if self.with_out_conv:
        x = self.out_conv(x)
    return x

self._binary_op的实现如下，其中self.global_pool是全局平均池化。

def _binary_op(self, x1, x2):
    x2_att = self.global_pool(x2).sigmoid()
    return x2 + x2_att * x1

最后的self.out_conv是Conv+BN+ReLU的组合，对应图6中的R-C-B。注意图6中只有第一个GP和最后一个GP后有R-C-B，中间两个GP后没有，即上面代码中self.with_out_conv=False。

SumCell和GlobalPoolingCell继承自同一个基类，forward函数是一样的。区别在于SumCell中的self._binary_op就是sum操作，如下

class SumCell(BaseMergeCell):
    def __init__(self, in_channels: int, out_channels: int, **kwargs):
        super().__init__(in_channels, out_channels, **kwargs)

    def _binary_op(self, x1, x2):
        return x1 + x2

此外，5个SumCell后都有R-C-B。

实验结果

和其他SOTA模型的对比如表1所示

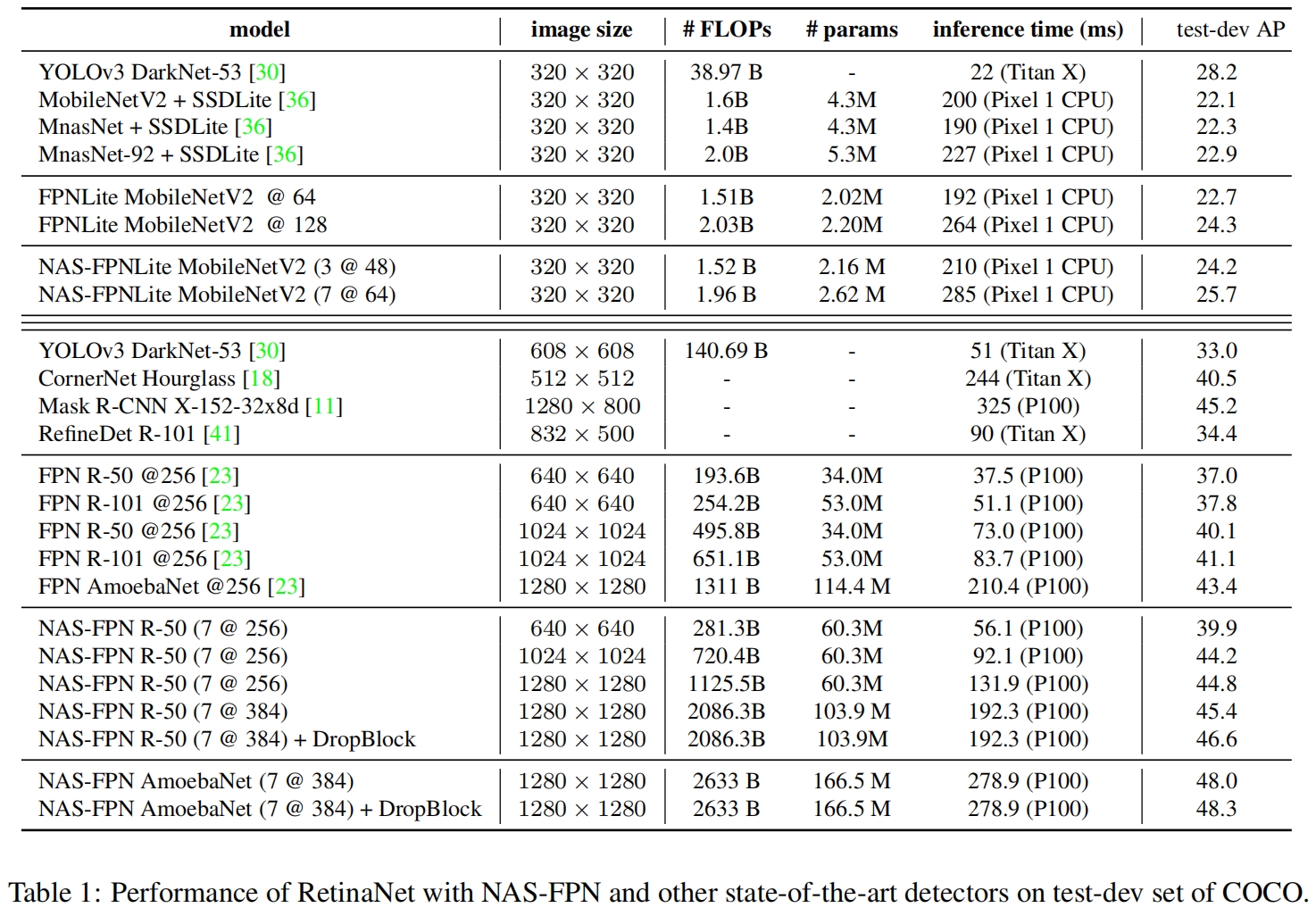
其中7@256表示NAS-FPN堆叠7次，通道数为256。

文中特别提到由于NAS-FPN的结构堆叠多层引入了更多的参数，需要一个合适的正则化方法来防止过拟合。本文采用DropBlock，具体介绍见DropBlock（NeurIPS 2018）论文与代码解析-CSDN博客。图10展示了DropBlock显著提升了NAS-FPN的性能。