C++系列-第3章循环结构-29-累乘和连除

在线练习：
http://noi.openjudge.cn/
https://www.luogu.com.cn/

累乘

累乘符号“Π”
∏是累乘符号，是希腊字母π的大写，读做pai，在数学上通常表示连乘,，小写π就表示圆周率。

链接：https://www.zhihu.com/question/26094736/answer/610713978

累加

∑是累加符号，是希腊字母σ的大写，读做sigma，在数学上通常表示连加,，小写σ就表示面密度（区别与体密度ρ和线密度η）。
函数的累积求和，n取[m, k]中的连续整数值，这个变量n可以换成其他任意字母，比如x。我们把下面的“n=m”和上面的“k”称作这个和式的下标。在上下文明确的情况下，下标可以省略。

求和符号同样可以表示无穷级数。

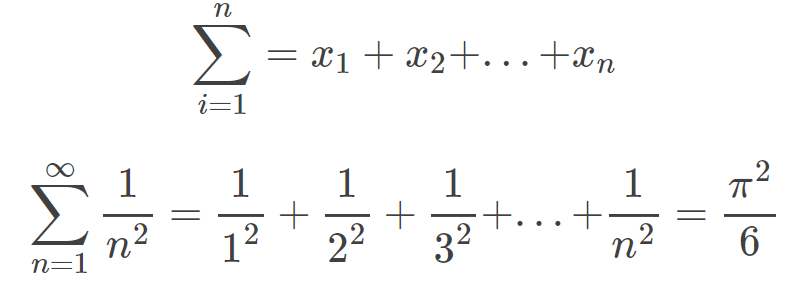
　求和与求积的用法是完全相同的。当下标不是连续整数时，下标也可以有不同的表达方式。“a|b”表示b能整除a，下面和式表示所有10的正因子的和。

排列组合与累加累乘

一：P 的由来

所谓排列组合，排列在组合之前，咱们要聊的第一个概念是“排列”，排列的英文是 Permutation 或者 Arrangement，因此在数学符号中，用 P 或者 A 表示都可以，二者意思完全一样。
我们常见的 P 右边会跟两个数字（或字母），右下角的数字 n 表示总数，右上角的数字 m 表示抽出的个数。整个符号的意思是“从 n 个人中，有顺序地抽出 m 个人的抽法数”，可以读作“P n 抽 m”。
那么，到底什么叫做有顺序的？
我们来举个数字很小的例子：比如：班里有三名同学，成绩前两名有几种可能性？咱们可以用乘法原理：选第一名有 3 种可能性，选第二名有 2 中可能性，因为第一名那个人不可能同时又是第二名了，将这两步相乘起来。（如果你不太理解乘法原理，可以看看下图直观列举的表示。）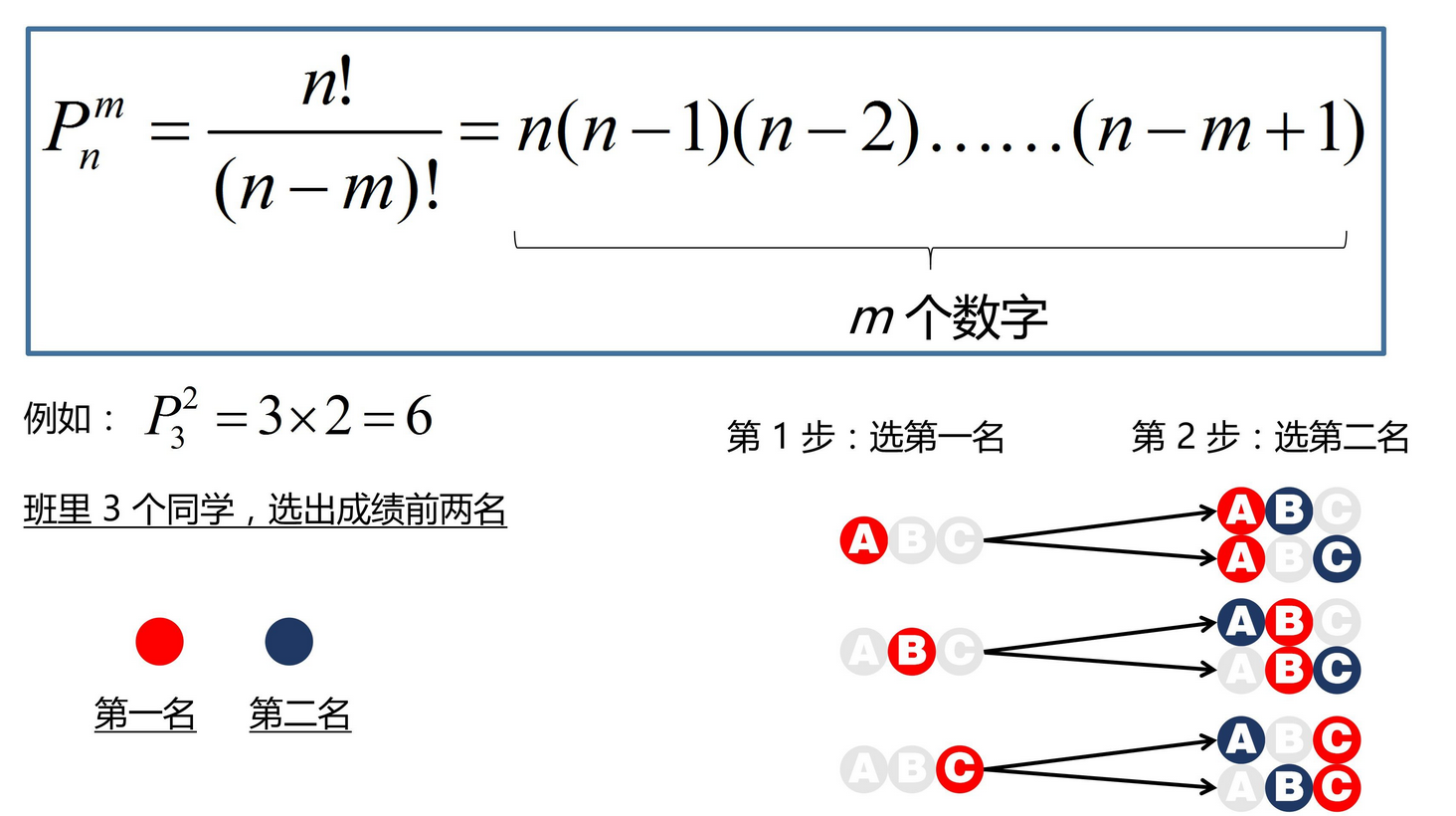

这个公式需要注意的是：虽然书上每次讲到这个公式时一般以阶乘（factorial）的形式给出，但实际计算中，往往不用阶乘。我的记法是：从大的数字开始往小乘，乘“小的数字那么多”个。

二：C 的由来

咱们聊的第二个概念是“组合”，它比排列更常用，组合的英文是 Combination，因此在数学符号中用 C 表示，美国和英国教材中，也常用“长括号”表示组合数。我们常见的 C 右边会跟两个数字（或字母），右下角的数字 n 表示总数，右上角的数字 m 表示抽出的个数。整个符号的意思是“从 n 个人中，不计顺序地抽出 m 个人的抽法数”，可以读作“C n 抽 m”。
那么，到底什么叫做不计顺序的？
我们也来举个例子🌰：
比如：班里有三名同学，选出两名代表参加年级会议有几种选法？

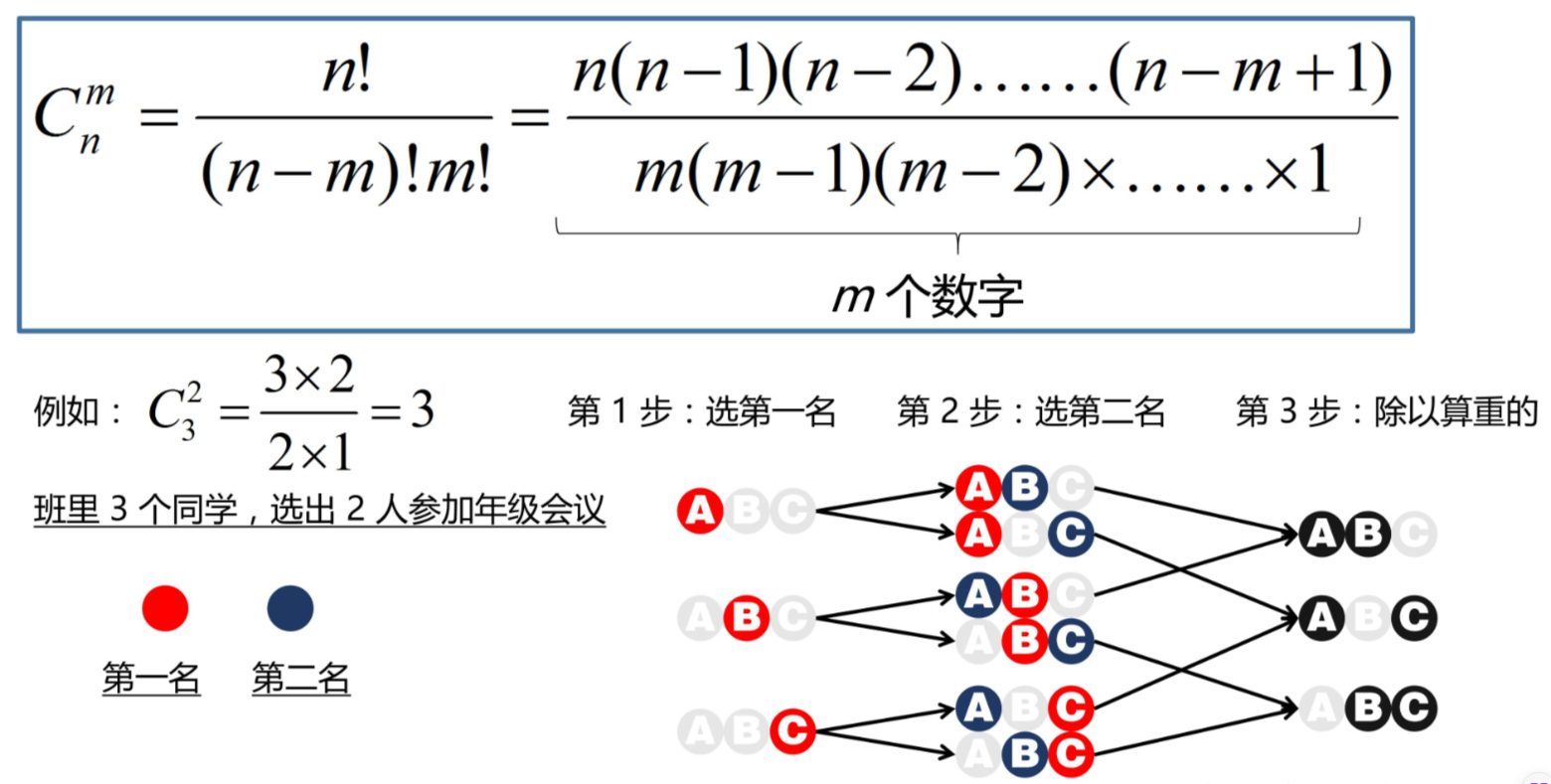
于是，组合数公式就是在排列数公式上除以一个 m！。但实际计算中，往往不用阶乘。我的记法是：从大的数字开始往小乘，乘“小的数字那么多”个，再除以“小的数字开始往小乘，乘小的数字那么多个”。

计算阶乘

题目描述

求 $n!$，也就是 $1\times 2\times 3?\times n$。

挑战：尝试不使用循环语句（for、while）完成这个任务。

输入格式

第一行输入一个正整数 $n$。

输出格式

输出一个正整数，表示 $n!$。

样例 #1

样例输入 #1

3

##3# 样例输出 #1

6

提示

数据保证，$1\le n\le 12$。

代码

#include<bits/stdc++.h>
using namespace std;
int n;
long long ans=1;//保险，虽然不会int爆
int main(){
	cin>>n;
	for(int i=1;i<=n;i++) ans*=i;
	cout<<ans;
	return 0;
}

输出为：

//#include<bits/stdc++.h>
#include<iostream> 
using namespace std;
int n;
long long ans=1;
int main(){
	cin>>n;
	if(1<=n){ans*=1;}
	if(2<=n){ans*=2;}
	if(3<=n){ans*=3;}
	if(4<=n){ans*=4;}
	if(5<=n){ans*=5;}
	if(6<=n){ans*=6;}
	if(7<=n){ans*=7;}
	if(8<=n){ans*=8;}
	if(9<=n){ans*=9;}
	if(10<=n){ans*=10;}
	if(11<=n){ans*=11;}
	if(12<=n){ans*=12;}
	cout<<ans;
	return 0;
}

输出为：

幂的末尾

题目描述

幂 $a^b$ 的末 $3$ 位数是多少？

输入格式

两个正整数 $a$，$b$。$1\le a\le 100$，$1\le b\le 10000$。

输出格式

从高位到低位输出幂的末三位数字，中间无分隔符。若幂本身不足三位，在前面补零。

样例 #1

样例输入 #1

2 3

样例输出 #1

008

样例 #2

样例输入 #2

7 2011

样例输出 #2

743

代码

这题暴力肯定不予考虑（一本坑能这么单纯？），那么让我们换一种思路。

方法一

#include <iostream>
//#include <cstdio>
using namespace std;
int main(){
	int a,b;
	cin>>a>>b;
	int ans=1;
	//要把 ans 设为 1 ，即为 a 的 0 次。
	for(int i=1;i<=b;i++){
		//i 要从 1~b ， 即为 a 的 b 次。
		ans*=a;
		ans%=1000;
	}
                       
	if(ans<10)//如果这个数为 1 位数，先输出 2 个 0，再输出 ans。
		cout<<"00"<<ans;
	else if(10<=ans&&ans<100)//如果这个数为 2 位数，输出 1 个 0，再输出 ans。
		cout<<"0"<<ans;
	else
		cout<<ans;
}

输出为：

方法二

因为它只想要最后三位，所以我们可以用 for 循环模拟幂运算，并且每一次循环都取余1000，这样可以得到它的后三位，并且在最后输出时补齐。

#include <iostream>
#include <cstdio>
using namespace std;
  
long long a, b, s = 1;
 
int main()
{
    cin >> a >> b;
    for(int i = 0;i < b;++i)
        s *= a, s %= 1000; //每乘一次模一次1000
    printf("%03lld", s); //补满3位的0
    return 0;
}

输出为：

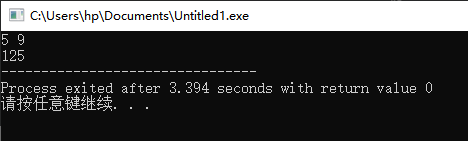
求小数的某一位

题目描述

分数 $\frac{a}{b}$ 化为小数后，小数点后第 $n$ 位的数字是多少？

输入格式

三个正整数 $a$，$b$，$n$，相邻两个数之间用单个空格隔开。$0<a\le b\le 100$，$1\le n\le 10000$。

输出格式

一个数字。

样例 #1

样例输入 #1

1 2 1

样例输出 #1

5

代码

方法一

#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
	int a,b,n;
	scanf("%d%d%d",&a,&b,&n);//读入
	double ans;
	ans=a*1.0/b;
	ans-=int(ans);//去除整数部分
	for(int i=1;i<n;i++)//循环 n-1 次
	{
		ans*=10.0;//小数浮出
		ans-=int(ans);//去除整数部分
	}
	ans*=10;//将要求的这一位浮出
	cout<<int(ans)<<endl;//整数部分此时就剩一位，即答案
	return 0;//好习惯
}

输出为：

方法二

#include <iostream>
using namespace std;
int main()
{
    int a,b,n;
    cin>>a>>b>>n;
    if(a==b){
        cout<<0;
        return 0;
    }
    for(int i=1;i<n;i++)
        a=a*10%b;//我在这里把a和r合起来用
    cout<<a*10/b;
	return 0;
}

输出为：

总结

本文是C++系列博客，主要讲述累乘和连除的计算