09、基于LunarLander登陆器的Dueling DQN强化学习（含PYTHON工程）

09、基于LunarLander登陆器的Dueling DQN强化学习（含PYTHON工程）

参考：

论文地址：https://proceedings.mlr.press/v48/wangf16.pdf

LunarLander复现：
07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）

08、基于LunarLander登陆器的DDQN强化学习（含PYTHON工程）

09、基于LunarLander登陆器的Dueling DQN强化学习（含PYTHON工程）

0、实践背景

gym的LunarLander是一个用于强化学习的经典环境。在这个环境中，智能体（agent）需要控制一个航天器在月球表面上着陆。航天器的动作包括向上推进、不进行任何操作、向左推进或向右推进。环境的状态包括航天器的位置、速度、方向、是否接触到地面或月球上空等。

智能体的任务是在一定的时间内通过选择正确的动作使航天器安全着陆，并且尽可能地消耗较少的燃料。如果航天器着陆时速度过快或者与地面碰撞，任务就会失败。智能体需要通过不断地尝试和学习来选择最优的动作序列，以完成这个任务。

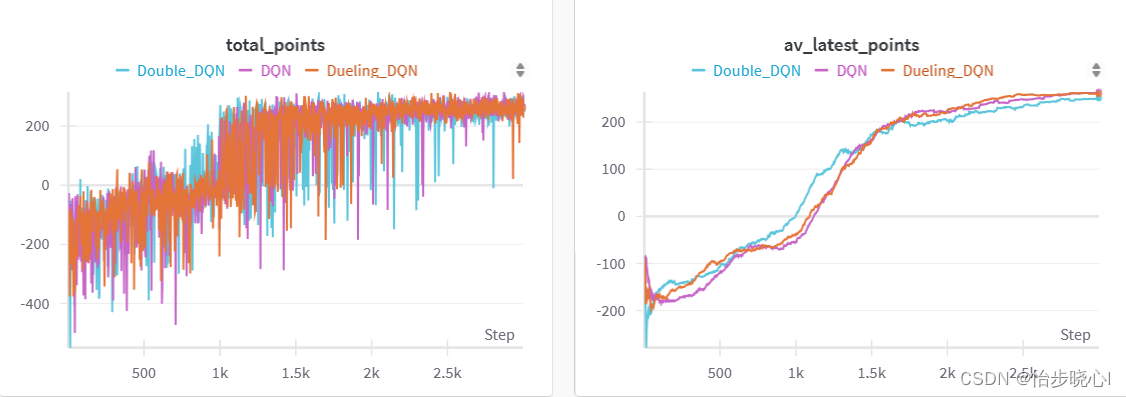
下面是训练的结果：

2、Dueling DQN实现原理

2.1 Dueling DQN基本知识

Dueling Deep Q Network(Dueling DQN)是对DQN算法的改进，有效提升了算法的性能。如果对DQN还不了解的话可以先参考：07、基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）

简单回顾一下DQN的基本知识，DQN的输出依赖于Q网络，其输出实际上是动作价值函数，该函数的维度等于动作空间的维度，就是你能执行的动作的数量。例如，动作价值函数的输出是[0.1,0.2,0.3]，我可以执行的动作是【上、左、右】，那么显而易见，执行右动作所获得的动作价值最高，那么我们所执行的动作应该是右(如果贪心策略的话)。

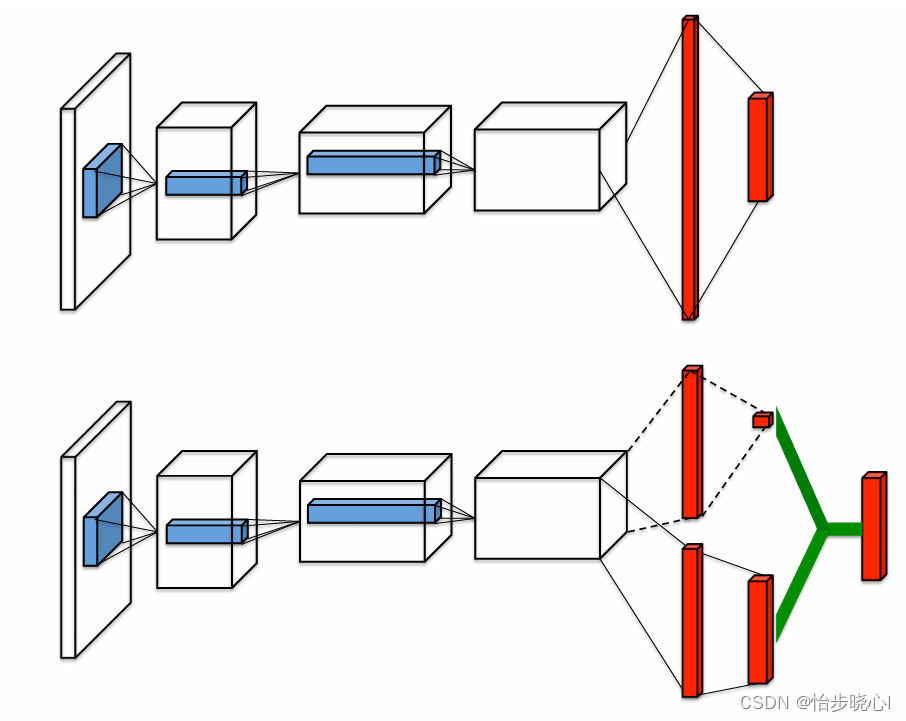
Dueling DQN是在DQN的基础上进行改进，其输出包含两个部分，分别是状态价值和动作优势。
显然，状态价值用于衡量当前状态的优劣，其实际上是一个数(标量)，而动作优势函数的维度等于动作空间的维度，代表执行每个动作能带来多大的相对优势。

动作优势函数的和为0，因此其实际上是一个相对值，表示某个动作相对其均值（所有动作价值的均值）能够带来多大的优势。

DQN和Dueling DQN的网络结构如下所示，可以看到Dueling DQN输出包含两个部分，将动作优势和其状态价值求和就是原来的动作价值函数Q（动作价值函数Q就是经典DQN的输出）。

更深入一点，状态价值函数V实际上就是动作价值函数Q的期望，也可以简单理解为状态价值函数是Q的均值：$V_{\pi }(s_t)=E\left[Q_{\pi }(s_t,A)\right]$。由此，Dueling DQN实际上是把输出拆成了两部分，一部分是Q的均值mean(Q)，一部分是Q-mean(Q)的部分，两部分的和就是Q函数，与DQN一致。

2.2 Dueling DQN能够带来性能提升的简单直觉

将原来的动作价值函数Q，拆分为状态价值函数mean(Q)和动作优势函数Q-mean(Q)有什么好处呢？在此举例：

存在一种情况，无论你采取任何动作，对结果的影响可能都并不关键。

例如，朱元璋开局一个碗，到发家致富建立大明，必然是发奋刻苦，抓住实际，因此，他的每一个动作的选择都至关重要，会对他的未来造成很大的影响。再例如，我开局10个亿，我每天吃吃喝喝，干啥都能享受生活，反正那么多米一辈子也用不完嘞。这种情况下，我采取什么动作已经不是很重要了，毕竟开局就在罗马。

因此，将原来的动作价值函数拆分为状态价值函数mean(Q)和动作优势函数Q-mean(Q)，是合理的，可以分辨当前的动作优势是自身动作带来的还是当前环境带来的，这样各司其职，效果也会更好。

关于“分辨当前的动作优势是自身动作带来的还是当前环境带来的”，还有一个方便读者理解的例子，例如我一届书生，进京赶考，考取功名当官了，那这种情况我获得的奖励大概来自自身的动作；但是如果我是宰相的儿子，也当官了，可能当前环境（我的爸爸是宰相）所造成的优势会更大一点。

3 Dueling DQN的代码实现

基于LunarLander登陆器的DQN强化学习案例（含PYTHON工程）已经给出了DQN的全部实现代码，Dueling DQN只是在网络构建上有所不同。Dueling DQN的网络构建代码如下所示：

def GenModelDuelingDQN(num_actions, input_dims, fc1, fc2, fc3):
    # define input
    input_node = tf.keras.Input(shape=input_dims)
    input_layer = input_node
    # define state value function(计算状态价值函数)
    state_value = tf.keras.layers.Dense(fc1, activation='relu')(input_layer)
    state_value = tf.keras.layers.Dense(1, activation='linear')(state_value)
    # state value and action value need to have the same shape for adding
    # 这里是进行统一维度的
    state_value = tf.keras.layers.Lambda(
        lambda s: tf.keras.backend.expand_dims(s[:, 0], axis=-1),
        output_shape=(input_dims,))(state_value)

    # define acion advantage (行为优势)
    action_advantage = tf.keras.layers.Dense(fc1, activation='relu')(input_layer)
    action_advantage = tf.keras.layers.Dense(fc2, activation='relu')(action_advantage)
    action_advantage = tf.keras.layers.Dense(fc3, activation='relu')(action_advantage)
    action_advantage = tf.keras.layers.Dense(num_actions, activation='linear')(action_advantage)
    # See Dueling_DQN Paper
    action_advantage = tf.keras.layers.Lambda(
        lambda a: a[:, :] - tf.keras.backend.mean(a[:, :], keepdims=True),
        output_shape=(num_actions,))(action_advantage)
    # 相加
    Q = tf.keras.layers.add([state_value, action_advantage])
    # define model
    model = tf.keras.Model(inputs=input_node, outputs=Q)
    return model

其中，使用tf.keras.layers.Lambda自定义网络层，lambda a: a[:, :] - tf.keras.backend.mean(a[:, :]就是实现动作优势函数的关键。但是，最终输出的还是Q，要把动作优势函数和状态函数两部分加起来。因此，其在训练过程中和DQN没有什么不同。

4 Dueling DQN效果

对于LunarLander登陆器这个环境，Dueling DQN没有带来非常明显的改善，也有可能是因为我没有调参数。