力扣日记12.19-【二叉树篇】二叉搜索树中的搜索
发布时间:2023年12月20日
力扣日记:【二叉树篇】二叉搜索树中的搜索
日期:2023.12.19
参考:代码随想录、力扣
700. 二叉搜索树中的搜索
题目描述
难度:简单
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
示例 1:
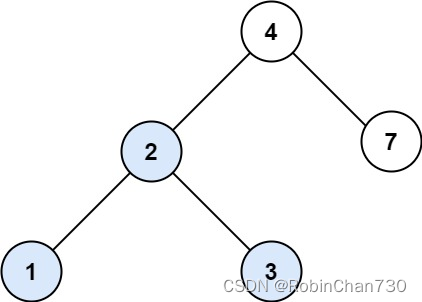
输入:root = [4,2,7,1,3], val = 2
输出:[2,1,3]
示例 2:
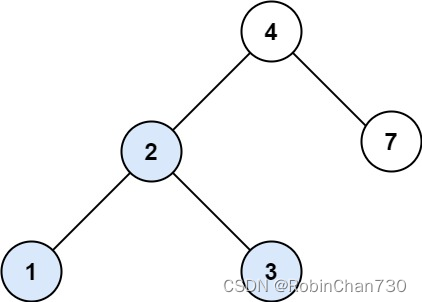
输入:root = [4,2,7,1,3], val = 5
输出:[]
提示:
- 树中节点数在 [1, 5000] 范围内
- 1 <= Node.val <= 10^7
- root 是二叉搜索树
- 1 <= val <= 10^7
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
#define SOLUTION 3
public:
#if SOLUTION == 1
// 没有利用 二叉搜索树 的特征
TreeNode* searchBST(TreeNode* root, int val) {
// 终止条件
if (root == nullptr) return nullptr;
// 中
if (root->val == val) return root;
// 左
TreeNode* left = searchBST(root->left, val);
if (left != nullptr && left->val == val) return left;
// 右
TreeNode* right = searchBST(root->right, val);
if (right != nullptr && right->val == val) return right;
return nullptr;
}
#elif SOLUTION == 2
// 利用 二叉搜索树 的特征
/*
二叉搜索树是一个有序树
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉排序树
*/
TreeNode* searchBST(TreeNode* root, int val) {
if (root == nullptr) return nullptr;
if (root->val == val) return root;
// 如果值比root->val大, 说明只有可能在右子树有
else if (root->val < val) {
// 只递归右子树
TreeNode* right = searchBST(root->right, val);
// 无论right是否为null, 都返回right
return right;
} else {
// 否则,递归左子树
TreeNode* left = searchBST(root->left, val);
return left;
}
}
#elif SOLUTION == 3
// 迭代法
TreeNode* searchBST(TreeNode* root, int val) {
// 模拟
while (root != nullptr) {
if (root->val == val) return root;
else if (root->val > val) root = root->left; // 如果值大了,则往左边搜索
else root = root->right; // 否则往右边
}
return root;
}
#endif
};
复杂度
时间复杂度:
空间复杂度:
思路总结
- 要注意二叉搜索树的特性:
- 二叉搜索树是一个有序树
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
- 因此在递归或者迭代时可以利用其特性,判断搜索方向
文章来源:https://blog.csdn.net/weixin_45847708/article/details/135090287
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 多核调度实验设计
- SSL VPN简介
- 【JVM基础】 JVM 如何加载一个类以及类加载机制
- TrustZone之强制隔离
- 以某一web系统为测试对象(若依RuoYi为例)-软件测试实验报告作业
- Redis设计与实现之简单的动态
- MyBatis的缓存
- 24岁,拿到18K,我真的很卷?
- 2. goLand安装及外配置参数通用用法
- #LLMOps##AIGC# Dify_构建本地知识库问答应用-生成Al应用的创新引擎 用于构建助手API和GPT的开源开发平台