线性回归原理

线性回归应用场景

• 房价预测

• 销售额预测

• 贷款额度预测

线性回归(Linear regression)是利用?回归方程对?一个或多个自变量(特征值)和因变量(目标值)之间?关系进行建模的一种分析方式。

• 期末成绩：0.7×考试成绩+0.3×平时成绩
• 房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价)?

我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型?。?

线性回归当中主要有两种模型，?一种是线性关系，另一种是非线性关系。?

?线性回归API

sklearn中， 线性回归的API在linear_model模块中

sklearn.linear_model.LinearRegression()

• LinearRegression.coef_：回归系数

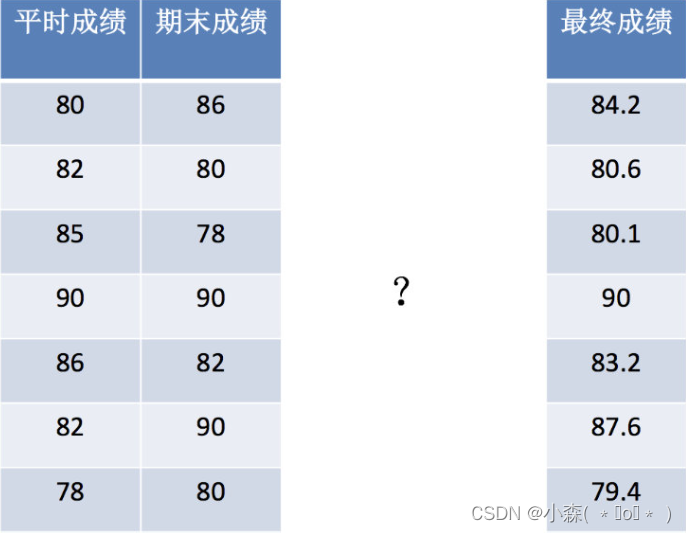
from sklearn.linear_model import LinearRegression

x = [[80, 86],
     [82, 80],
     [85, 78],
     [90, 90],
     [86, 82],
     [82, 90],
     [78, 80],
     [92, 94]]

y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]

# 实例化
estimator = LinearRegression()
# 使用fit方法进行训练
estimator.fit(x,y)
print(estimator.coef_)
# 未知样本预测
print(estimator.predict([[100, 80]]))

#
[0.3 0.7]
[86.]

1. LinearRegression.fit 表示模型训练函数
2. LinearRegression.predict 表示模型预测函数
3. 线性回归模型的目标：通过学习得到线性方程的这两个权值，y=kx+b中，得到k和b两个权值

损失函数?

• 衡量机器学习模型性能
• 损失函数可以计算预测值与真实值之间的误差，误差越小说明模型性能越好。

• 确定损失函数之后， 我们通过求解损失函数的极小值来确定机器学习模型中的参数。

X = [0.0, 1.0, 2.0, 3.0]

y = [0.0, 2.5, 3.3, 6.2] ? ? ?

上面的数据中，X与y的关系可以近似的表示为一元线性关系， 即 y = WX?

训练线性回归模型模型的过程实际上就是要找到一个合适的W??

我们将距离定义为：dis=y1-y2，可以计算出当W=5.0时预测的误差分别为：0、2.5、6.7、8.8

将上面所有点的预测误差相加得到18，误差有些大，模型还有调整的空间，令W=2时计算出误差为0，但实际情况除了d0之外其余点均存在预测误差。

所以我们不能简单的将每个点的预测误差相加得到误差值。

回归问题的损失函数通常用下面的函数表示：

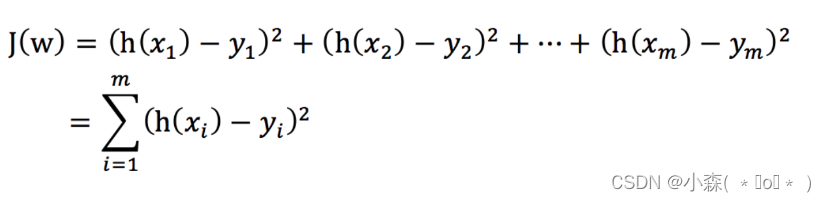
1. yi?为第i个训练样本的真实值
2. h(xi) 为第i个训练样本特征值组合预测函数

损失函数在训练阶段能够指导模型的优化方向，在测试阶段能够用于评估模型的优劣。?

import numpy as np
from sklearn.linear_model import LinearRegression

x = np.asarray([[80, 86],
                [82, 80],
                [85, 78],
                [90, 90],
                [86, 82],
                [82, 90],
                [78, 80],
                [92, 94]])

# 目标值
y = np.asarray([84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]).transpose()

# 使用 LinearRegression 求解
estimator = LinearRegression(fit_intercept=True)  
# 设置参数fit_intercept=True意味着在训练模型时会包含一个截距项（也就是y轴截距），这是线性回归中# # 通常需要的一个参数，用于捕捉数据在没有特征影响时的基准水平
estimator.fit(x, y)
print(estimator.coef_)

#
[0.3 0.7]

?梯度下降

梯度下降法的基本思想可以类比为一个下山的过程。?

我们设想自己站在一座山（目标函数的等高线图）上，我们的目标是最小化这个函数值，也就是说，我们要找到这座山的最低点或山谷。

梯度代表了函数在当前位置的斜率或者方向导数，它指向函数增长最快的方向。

而梯度下降法则是沿着梯度的相反方向前进，这就好比我们在山上下行时选择最陡峭下降的路径。每一步，我们都根据当前位置的梯度调整步伐，以期逐步逼近最低点，即函数的最小值。

通过不断迭代更新参数，使得每次迭代后目标函数值逐渐减小，最终达到或接近全局最小值的位置，这就是梯度下降法的核心思想。我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值。

在多变量函数中，梯度是一个向量，有方向，梯度的方向就指出了函数在给定点的上升最快的方向

单变量函数的梯度下降

函数 f(x) = x^2。要找到这个函数的最小值，我们可以使用梯度下降法：

1. 首先，选择一个初始点 x0（比如 x0 = 5）。
2. 计算在该点的梯度（导数）：f'(x0) = 2x0 = 25 = 10。
3. 梯度下降法要求我们沿负梯度方向前进，也就是朝函数值减少的方向移动。通常会设置一个学习率（步长）α，用来控制每一步走的距离。比如 α = 0.1。
4. 更新 x 的值：x1 = x0 - α * f'(x0) = 5 - 0.1 * 10 = 4。
5. 在新的位置 x1 处重复步骤2-4，直到达到某个停止条件。

经过多次迭代后，我们会发现 x 的值逐渐接近于0，因为函数 f(x) = x^2 在 x=0 处取得全局最小值?

在下山类比中，学习率α就好比我们每一步走的距离。如果α值设置得过大（步子迈得太大），可能会导致我们在函数曲面上“跨越”过最小值点，从而无法收敛到最优解，甚至可能使得损失函数值震荡加剧，不稳定性增加。

相反，如果α值设置得过小（步子迈得太小），虽然算法会更加稳定，但收敛速度会大大降低，需要更多次迭代才能找到最小值。

在二维或者三维图像中，学习率α体现在每次更新后沿负梯度方向移动的距离上，直观地表现为从一个点到下一个点的直线段长度。

?多变量函数的梯度下降

回归评估

平均绝对误差Mean Absolute Error

?

n 为样本数量, y 为实际值,?y^?为预测值?，越小模型预测约准确

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test,y_predict)

均方误差Mean Squared Error

越小模型预测约准确

from sklearn.metrics import mean_squared_error
mean_squared_error(y_test,y_predict)

?均方根误差Root Mean Squared Error?

?

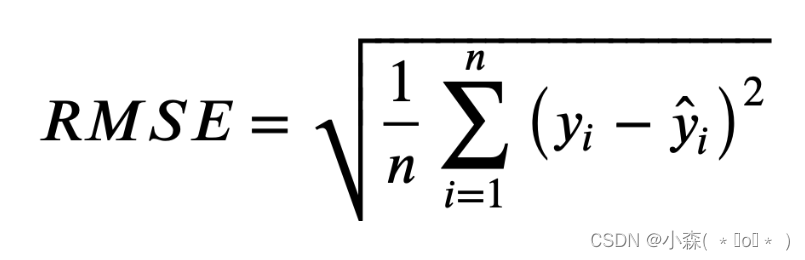?越小模型预测约准确，RMSE 是 MSE 的平方根，有时候比MES更有用。

RMSE 会放大预测误差较大的样本对结果的影响，而 MAE 只是给出了平均误差，由于 RMSE 对误差的平方和求平均再开根号，大多数情况下RMSE>MAE。

数据中有少数异常点偏差很大，如果此时根据 RMSE 选择线性回归模型，可能会选出过拟合的模型来，数据中的异常点极少，选择具有最低 MAE 的回归模型可能更合适。