MATLAB实现相关性分析数学建模算法

相关性分析是一种统计方法，用于确定两个或多个变量之间的关系强度和方向。相关性分析可以帮助我们了解变量之间的相关程度，从而帮助我们预测一个变量如何受到另一个变量的影响。相关性分析通常使用相关系数来衡量变量之间的关系。常用的相关系数包括Pearson相关系数Spearman等级相关系数和Kendall等级相关系数。Pearson相关系数用于衡量两个连续变量之间的线性关系，Spearman和Kendall等级相关系数用于衡量两个变量之间的等级关系。相关性分析可以帮助我们确定两个变量之间的关系是正相关、负相关还是无关。正相关意味着两个变量的值一起增加或减少，负相关意味着一个变量的值增加时，另一个变量的值减少，无关意味着两个变量之间没有明显的关系。相关性分析在许多领域都有广泛的应用，包括经济学、社会科学、医学和工程等。通过相关性分析，我们可以更好地理解变量之间的关系，从而做出更准确的预测和决策。

clear;clc
load 'physical fitness test.mat'  %文件名如果有空格隔开，那么需要加引号
% https://ww2.mathworks.cn/help/matlab/ref/corrcoef.html
%% 统计描述
MIN = min(Test);  % 每一列的最小值
MAX = max(Test);   % 每一列的最大值
MEAN = mean(Test);  % 每一列的均值
MEDIAN = median(Test);  %每一列的中位数
SKEWNESS = skewness(Test); %每一列的偏度
KURTOSIS = kurtosis(Test);  %每一列的峰度
STD = std(Test);  % 每一列的标准差
RESULT = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]  %将这些统计量放到一个矩阵中表示
%% 计算各列之间的相关系数
% 在计算皮尔逊相关系数之前,一定要做出散点图来看两组变量之间是否有线性关系
% 这里使用Spss比较方便: 图形 - 旧对话框 - 散点图/点图 - 矩阵散点图
R = corrcoef(Test)   % correlation coefficient
%% 假设检验部分
x = -4:0.1:4;
y = tpdf(x,28);  %求t分布的概率密度值 28是自由度  
figure(1)
plot(x,y,'-')
grid on  % 在画出的图上加上网格线
hold on  % 保留原来的图，以便继续在上面操作
% matlab可以求出临界值，函数如下
tinv(0.975,28)    %    2.0484
% 这个函数是累积密度函数cdf的反函数
plot([-2.048,-2.048],[0,tpdf(-2.048,28)],'r-')
plot([2.048,2.048],[0,tpdf(2.048,28)],'r-')
%% 计算p值
x = -4:0.1:4;
y = tpdf(x,28);
figure(2)
plot(x,y,'-')
grid on 
hold on
% 画线段的方法
plot([-3.055,-3.055],[0,tpdf(-3.055,28)],'r-')
plot([3.055,3.055],[0,tpdf(3.055,28)],'r-')
disp('该检验值对应的p值为：')
disp((1-tcdf(3.055,28))*2)  %双侧检验的p值要乘以2
%% 计算各列之间的相关系数以及p值
[R,P] = corrcoef(Test)
% 在EXCEL表格中给数据右上角标上显著性符号吧
P < 0.01  % 标记3颗星的位置
(P < 0.05) .* (P > 0.01)  % 标记2颗星的位置
(P < 0.1) .* (P > 0.05) % % 标记1颗星的位置
% 也可以使用Spss操作哦 看我演示
%% 正态分布检验
% 正态分布的偏度和峰度
x = normrnd(2,3,100,1);   % 生成100*1的随机向量，每个元素是均值为2，标准差为3的正态分布
skewness(x)  %偏度
kurtosis(x)  %峰度
qqplot(x)
% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
[h,p] = jbtest(Test(:,1),0.01)
% 用循环检验所有列的数据
n_c = size(Test,2);  % number of column 数据的列数
H = zeros(1,6);  % 初始化节省时间和消耗
P = zeros(1,6);
for i = 1:n_c
    [h,p] = jbtest(Test(:,i),0.05);
    H(i)=h;
    P(i)=p;
end
disp(H)
disp(P)
% Q-Q图
qqplot(Test(:,1))
%% 斯皮尔曼相关系数
X = [3 8 4 7 2]'  % 一定要是列向量哦，一撇'表示求转置
Y = [5 10 9 10 6]'
% 第一种计算方法
1-6*(1+0.25+0.25+1)/5/24
% 第二种计算方法
coeff = corr(X , Y , 'type' , 'Spearman')
% 等价于：
RX = [2 5 3 4 1]
RY = [1 4.5 3 4.5 2]
R = corrcoef(RX,RY)
% 计算矩阵各列的斯皮尔曼相关系数
R = corr(Test, 'type' , 'Spearman')
% 大样本下的假设检验
% 计算检验值
disp(sqrt(590)*0.0301)
% 计算p值
disp((1-normcdf(0.7311))*2) % normcdf用来计算标准正态分布的累积概率密度函数
% 直接给出相关系数和p值
[R,P]=corr(Test, 'type' , 'Spearman')

部分运行结果如下所示：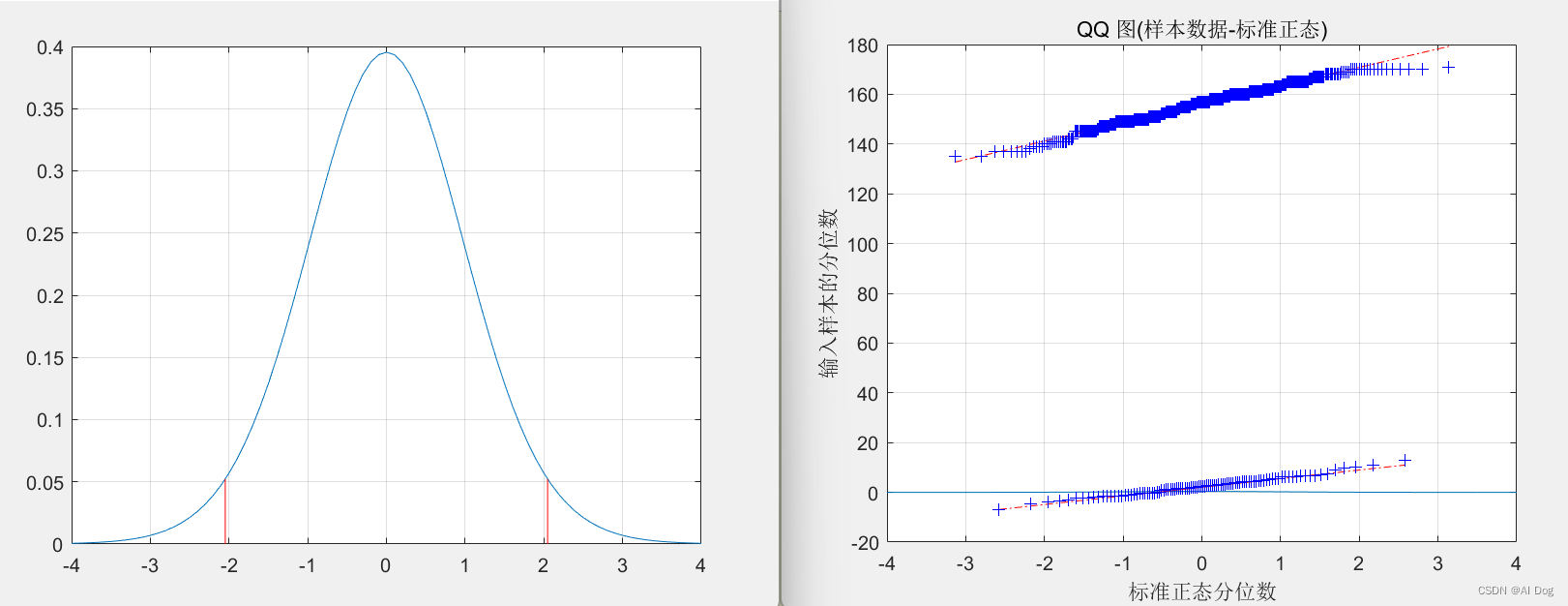

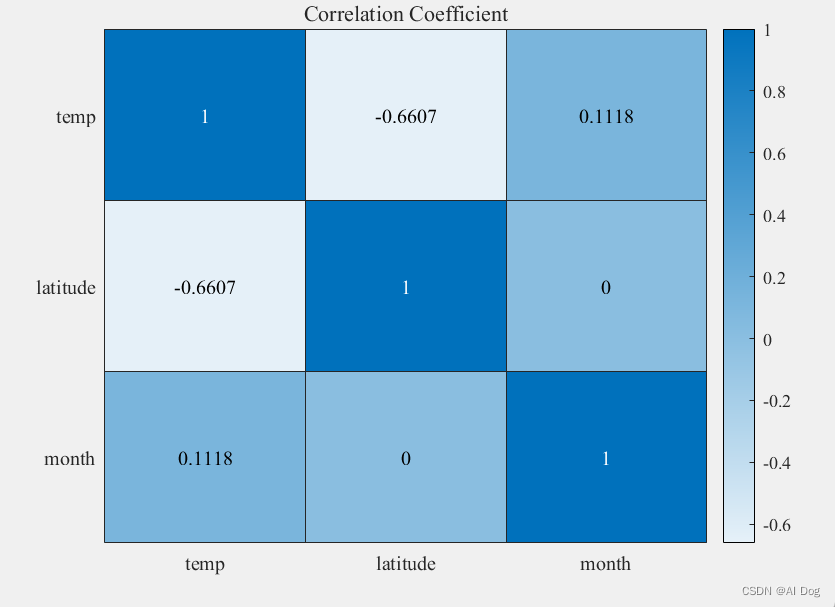
绘制相关系数热力图：

% 自己给定相关系数，自己定义热力图颜色
% 作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
rho = corr(data, 'type','spearman');
% 绘制热图
string_name={'temp','latitude','month'};
xvalues = string_name;
yvalues = string_name;
h1 = heatmap(xvalues,yvalues, rho, 'FontSize',10, 'FontName','Times New Roman');
h1.Title = 'Correlation Coefficient';
% h1.ColorbarVisible = 'off';
%map = [1 1 1; 1 1 0; 0.5 1 0.4; 0.2 0.85 0.2; 0.4 0.7 1; 0.2 0.5 0.8]; % 自己定义颜色
%colormap(map)
% saveas(gcf,sprintf('wine相关系数热图_自定义.jpg'),'bmp'); %保存图片