MIT_线性代数笔记:第 19 讲 行列式公式和代数余子式
我们已经认识到了行列式的性质,应该推导出其公式了。
行列式公式 Formula for the determinant
行列式有如下三个性质:
- det( I )=1。
- 如果交换行列式的两行,则行列式的数值会反号。
- 行列式是“矩阵的行”的线性函数。
从这三条性质可以推导出后续的七条性质,从这十个性质出发可以得到二阶方
阵的行列式公式:
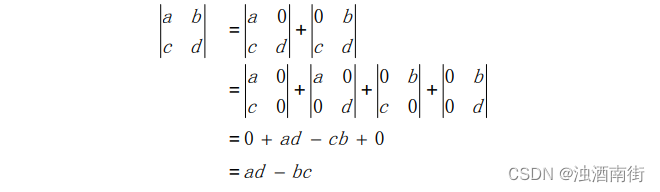
通过性质 3 对 n 阶矩阵的行列式进行拆分,我们可以得到所有只包含 n 个非零元素的行列式,对于二阶行列式我们从 1 个拆分为 2 个,然后拆分成 4 个。而对于三阶矩阵我们从 1 个拆分成 3 个,然后拆分成 9 个,最后要拆分成 27 个。但最终这些行列式中有很大一部分等于 0。
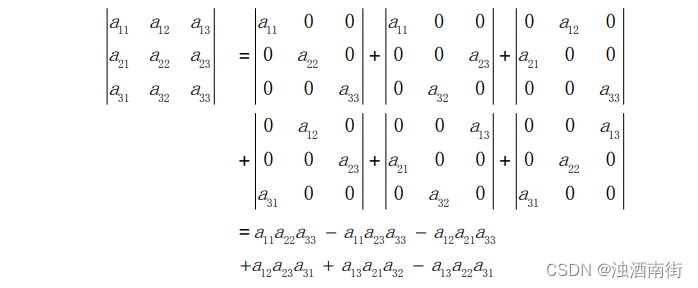
每一个拆分出来的非 0 行列式都是在每行每列都有且只有一个元素,就如同置换矩阵的元素分布。应用性质 3 可以将元素从行列式中提出来,而置换矩阵的行列式值为+1 或者-1,因此可以给出行列式的公式。n 阶拆分矩阵非 0 行列式的个数的计算方法就如同计算置换矩阵的个数一样,第一行放置一个非 0 元素的位置有 n 个选择,第二行为 n-1 个……。最后得到共 n!个矩阵。
对于拆分得到的三阶矩阵,元素从上至下朝向右侧方向的,其行列式的数值为正,朝向左侧方向的则为负。但是这个规律只适用于三阶矩阵,不适用于高阶矩阵。

其中列标号(α, β, γ……ω)是列标号(1, 2, 3……n)的某个排列。比如说对于单位阵而言,只有α=1,β=2……ω=n 所得到的行列式为+1,其它都为零,所以单位阵的行列式为 1。
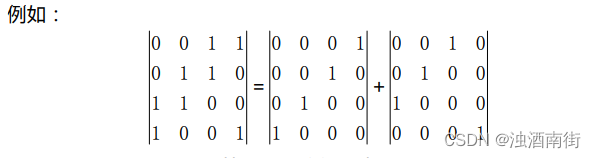
列标号取(4,3,2,1)得到第一个拆分行列式,符号为正,因为只要经过两次交换就能变为(1,2,3,4)。第二个为(3,2,1,4),因为只需交换一次就可变为正序,所以符号为负。因此本行列式为 0。
代数余子式 Cofactor formula
代数余子式是用较小的矩阵的行列式来写出 n 阶行列式的公式。
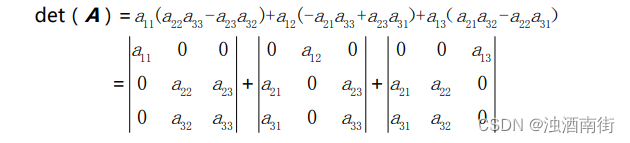
将原公式中属于矩阵第一行的 a1j提出来,其系数即为代数余子式,是一个低阶行列式的值。这个低阶行列式是由原矩阵去掉 a1j所在的行和列组成的。
对矩阵中任意元素 aij而言,其代数余子式 Cij就是矩阵的行列式的公式中 aij的系数。Cij等于原矩阵移除第 i 行和第 j 列后剩余元素组成的 n-1 阶矩阵的行列式数值乘以(-1)i+j。(Cij在 i+j 为偶数时为正,奇数时为负数。)

对于矩阵行列式的计算,消元的得到主元是一个很好的方法,与之相比行列式的展开公式较为复杂,而代数余子式的方法介于两者之间,它的核心想法是通过降阶来将原来的行列式展开成更简单的行列式。
举三对角阵(tridiagonal matrix)为例,它除了对角线和对角线两侧相邻的元素之外,其它元素均为 0。
例如由 1 组成的 4 阶三对角阵为

从矩阵的特殊结构我们可以得到:
∣
A
n
∣
=
∣
A
n
?
1
∣
?
∣
A
n
?
2
∣
\begin{vmatrix} A_n \end{vmatrix} =\begin{vmatrix} A_{n-1} \end{vmatrix} -\begin{vmatrix} A_{n-2} \end{vmatrix}
?An??
?=
?An?1??
??
?An?2??
?
由 1 组成的 n 阶三对角阵的行列式从 1 阶开始按照 1,0,-1,-1,0,1 进行循环。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 博客引擎 hugo intro 入门介绍+安装笔记
- MySql踩坑记录 DATE_FORMAT函数
- Python基础(二十、捕获异常)
- 如何使用ActiveMQ:一篇技术指南
- Git:远程仓库的使用
- 【Dubbo】RPC框架dubbo入门
- k8s之HPA
- 红帽秘笈,第三十三jinja2模板的使用
- docker搭建kali及安装oneforall
- nifi详细介绍--一款开箱即用、功能强大可靠,可用于处理和分发数据的大数据组件