数据结构——第六章 图——有向无环图

可以对比二叉树

有向无环图（DAG图）：一个有向图中不存在环，则称之为有向无环图。

DAG图的作用：描述含有公共子式的表达式的工具。

例如：((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)

上面的式子可以利用二叉树来表示。

首先先确定式子中运算顺序，

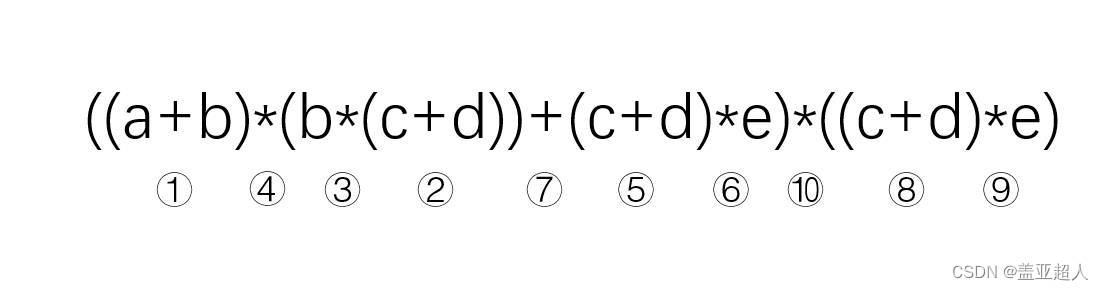
?然后利用二叉树的中序遍历画二叉树

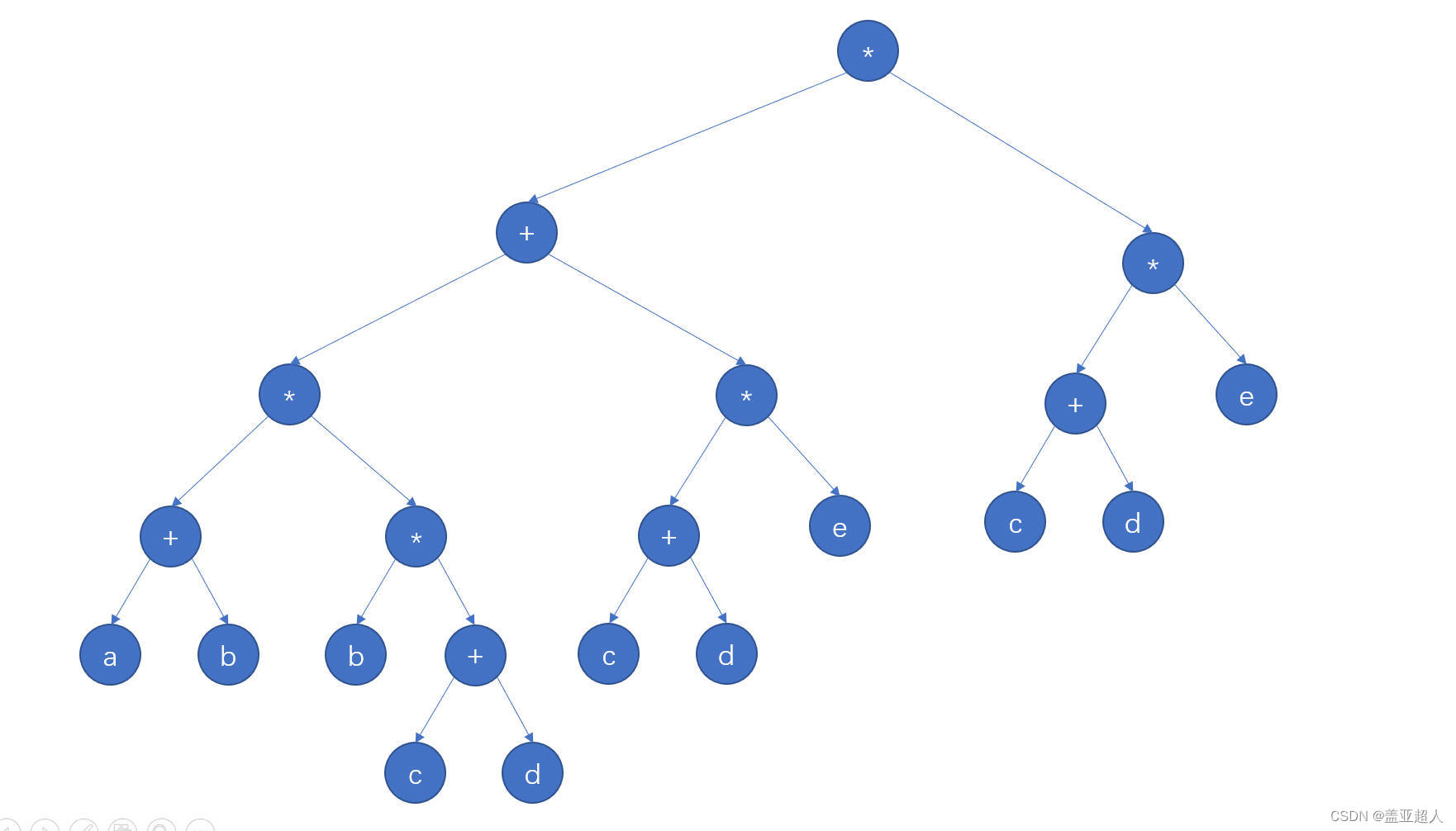
由上面的二叉树可以发现，里面有一些重复的分支（c+d)、(c+d)*e，,,

这样画图的时候比较耗费空间，在寸土寸金的年代，怎么要可以在节省空间的情况下又不改变图要表达的意思呢？答：将相同的部分设为共享子式，当有需要的时候调用它就行了。于是有向无环图就诞生了。

利用有向无环图可以实现对相同子式的共享，从而节省存储空间。

那怎么画有向无环图呢？

第一步：把各个操作数不重复的排成一排 （见图一）

第二步：标出各个运算符的生效顺序（先后顺序可能会不同，但是只要符合运算法则就不伤大雅）

第三步：按顺序加入运算符，要分层加入。

?

第四步：从低向上逐层检查同层的运算符是否可以合体。

?

最后整理一下

?

?