力扣【四数之和】

?一、题目描述

18.?四数之和

给你一个由?n?个整数组成的数组?nums?，和一个目标值?target?。请你找出并返回满足下述全部条件且不重复的四元组?[nums[a], nums[b], nums[c], nums[d]]?（若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d?< n
• a、b、c?和?d?互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按?任意顺序?返回答案 。

二、题目解析

算法思想：排序+双指针

1、依次固定一个数a；

2、在a后面的区间内，用“三数之和”找到三个数，使用这三个数的和等于target - a即可

同理，对于三数之和的算法：

1、依次固定一个数b；

2、在b后面的区间内，利用“双指针”找到两个数，是这两个数的和等于target - a - b

处理细节问题：

1、不重复

注意这里的去重和三数之和不同，这里需要多一组去重，在确定a时也是需要判断是否重复，其余去重操作和判断三数之和是一样。

2、不漏

与三数之和一样，在找到满足题目条件的一组元素之后，需要继续寻找。

注意：

这里的数据有溢出的风险，不开long long见祖宗~

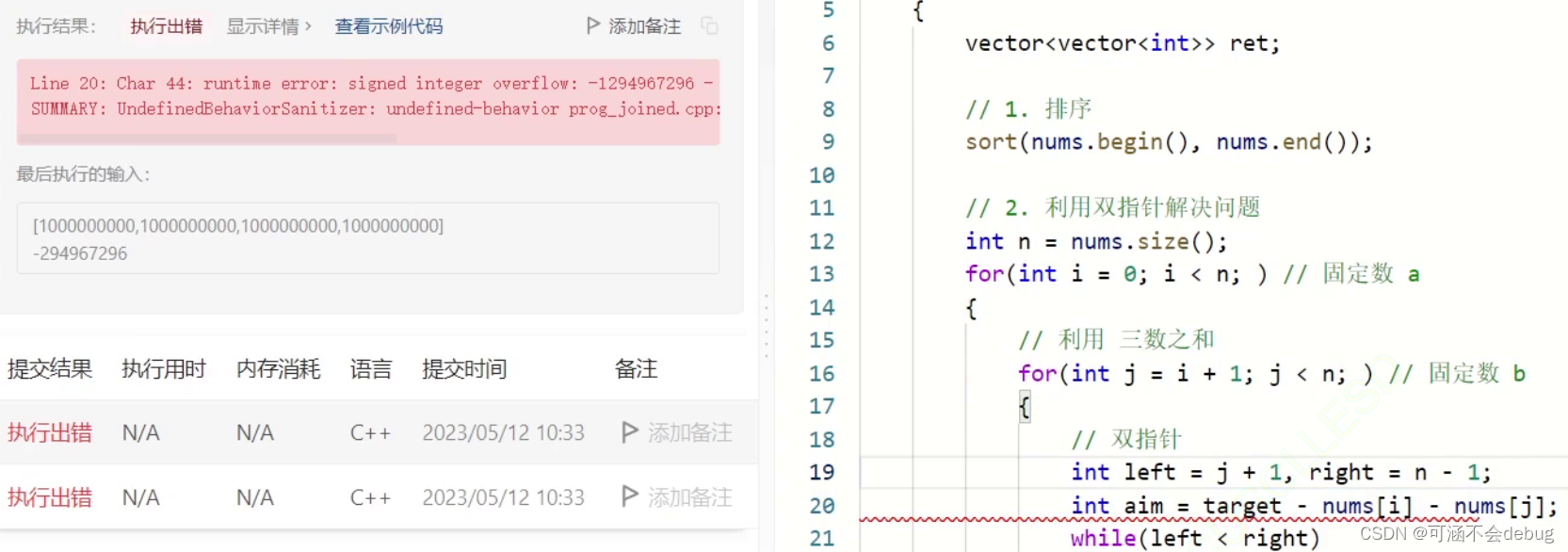
三、原码

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> ret;
        //1、先排序
        sort(nums.begin(),nums.end());
        //2、利用双指针解决
        int n = nums.size();
        for(int i = 0;i<n;)
        {
            //下面是三数之和
            for(int j = i+1;j<n;)
            {
                //防止数据溢出，开long long
                long long target2 = (long long)target - nums[i] - nums[j];
                int left = j+1;
                int right = n-1;
                while(left < right)
                {
                    int sum = nums[left] + nums[right];
                    if(sum > target2) 
                        right--;
                    else if(sum < target2) 
                        left++;
                    else
                    {
                        ret.push_back({nums[i],nums[j],nums[right],nums[left]});
                        left++;
                        right--;
                        //去重left right
                        while(left < right && nums[left] == nums[left-1]) left++;
                        while(left < right && nums[right] == nums[right+1]) right--;
                    }
                }
                //去重j
                j++;
                while(j<n && nums[j] == nums[j-1]) j++;
            }
            //去重i
            i++;
            while(i<n && nums[i] == nums[i-1]) i++;
        }
        return ret;
    }
};