链表？细啊！超详细的知识点总结！

链表

定义：链表是一种递归的数据结构，它或者为空（null)，或者是指向一个结点（node）的引用，该结点含有一个泛型的元素和一个指向另一条链表的引用。

? 其实链表就是有序的列表，它在内存中不一定是连续存储的。我们把它画成连起来是逻辑结构的，而不是内存中的实际情况。

? 链表是一种兼具递归和迭代性质的数据结构

特点：

1. 链表是以节点的方式来存储,是链式存储

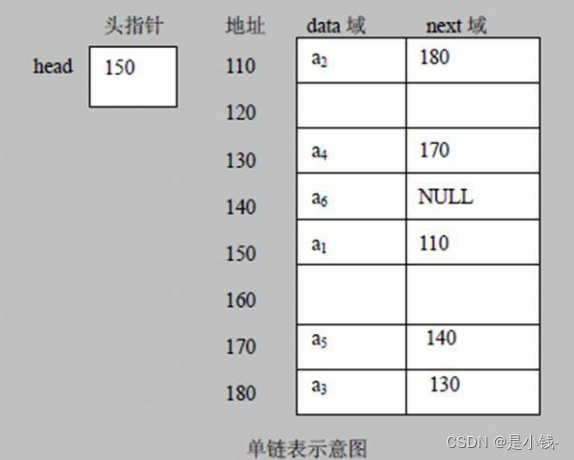
2. 每个节点包含 data 域， next 域（指向下一个节点）

3. 链表的各个节点不一定是连续存储。

4. 链表分带头节点的链表和没有头节点的链表，根据实际的需求来确定

——————

一些概念：

【头节点：在链表的第一个节点之前会额外增设一个节点，该节点的数据域一般不存放数据】

【首元节点：链表中第一个元素所在的节点，它是头节点后边的第一个节点】

（都首元了，元就是元素，第一个有元素的节点）

【头指针：永远指向链表中第一个节点的位置，有头节点就指向头节点】
（下图网上找的）

单链表的应用实例

构造链表：

? 根据递归定义，一个Node类型的变量就可以表示一条链条。只需要保证它的值是null或者指向另外一个Node对象且该对象的next域指向了另外一条链条即可。

public class Node {

    //数据域 item(参数类型)
    public Item data; 
    
    //指针域，指向下一个节点
    public Node next;

    public Node() {
    }

    public Node(Item data) {
        this.data = data;
    }

    public Node(Item data, Node next) {
        this.data = data;
        this.next = next;
    }
}

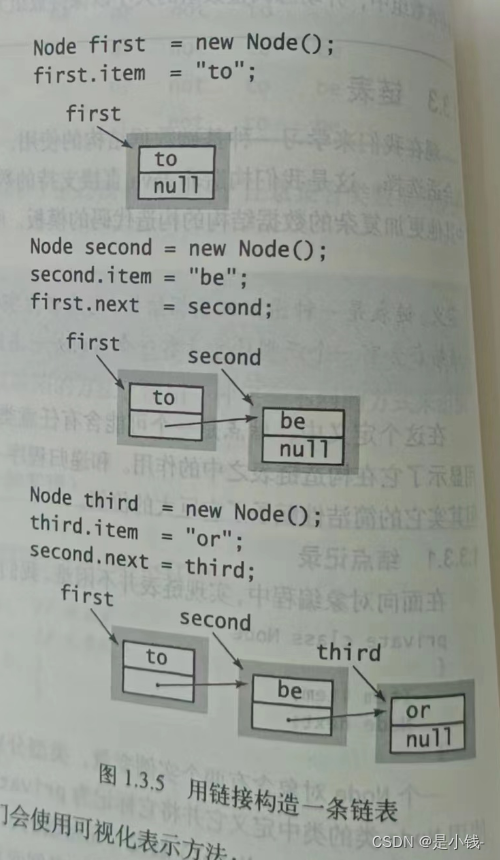
	// 创建一些节点
	Node first = new Node();
	Node second = new Node();
	Node third = new Node();
	// 设置所需要的值
	first.data = "to";
	second.data = "be";
	third.data = "or";
//当然这样直接有参构造也行： Node newNode = new Node(value);

	// 设置next域来构造链表
	first.next = second;
	second.next = third;

注意：third.next是null，这个是创建时候被初始化的值。链表表示的是一列元素。first表示的序列是to，be，or。数组也可以表示：String[] s = {“to”，“be”，“or”}。

在表头插入元素：

向链表中插入一个新的节点，最简单的就是链表的开头。

实现思路：

? 1.找到当前链表的尾节点

? 2.将最后这个节点的 next 指向新的要加入的节点

public void addFirst(item value) {
    //初始化要加入的节点
    Node newNode = new Node(value);
	//因为 head 节点是不能动，因此我们需要一个辅助节点来遍历整个链表
	Node temp = head;
	//遍历链表，找到尾节点的位置
	while(temp.next == null) {
		//如果没有找到最后, 将将 temp 后移
		temp = temp.next;
	}
	//当退出 while 循环时，temp 就指向了链表的最后
	//将最后这个节点的 next 指向 新的节点
	temp.next = newNode;
}             

插入节点：

1.因为要插入到指定位置，所以需要有位置相关的判断属性。然后进行相关判断，找到插入的位置

2.设置一个辅助指针遍历链表，去找要插入位置的上一个节点。因为这样节点有next域，这样子才可以将插入的节点前后链接起来。

(比如2个节点，要插在中间，newNode.next—>后一个节点，让前一个节点next—>newNode即可。注意顺序，因为先前一个节点next—>newNode，这样子后面newNode.next—>后一个节点是通过等于前一个节点.next。这样子会出错）

这里可以一开始在节点添加一个判断属性，或者额外定义一个值，记录遍历的位置

// index 要插入的位置
public void insert(item val, int index) {
        Node newNode = new Node(val);
        if (index == 0) {
            newNode.next = head;
            head = newNode;
        } else {
            Node temp = head;
            // 通过遍历，找到插入位置的上一个节点
            // 当i = index - 1 时，也代表temp就是要插入点的上一个节点的位置了
            for (int i = 0; i < index - 1 && temp != null; i++) {
                temp = temp.next;
            }
            // 当 temp 指向了空节点,意味着已经到达了链表的末尾,仍没有找到位置
            if (temp == null) {
                System.out.println("Index out of bound!");
                return;
            }
            // 插入节点的指向等于了上一个节点的指向
            newNode.next = temp.next;
            // 然后
            temp.next = newNode;
        }
    }

也可以创建一个变量记录当前遍历位置 location，用来判断到达的位置：

int location = 0;
while (temp.next != null) {
	// 找到要插入位置的前一个节点
	if ((index - 1) == location) {
    	newNode.next = temp.next;
        temp.next = newNode;
    	return;
    }
	location++;
	temp = temp.next;
}

删除节点：

从表头删除节点：即删除首节点，直接让头指针指向原本的下一个节点即可。

first = first.next;

指定删除具体某个节点：

和指定位置插入节点原理相似，只是删除是让前一个节点的next域指向删除节点的后一个节点，即：temp.next = temp.next.next

public void delete(Node head, int index) {
    // 临时节点
    Node temp = head;
    for (int i = 0; i < (index - 1) && temp != null; i++) {
        temp = temp.next;
    }
    // 删除
    // 如果 temp.next 为 null，则说明当前节点是链表的最后一个节点，此时再执行 temp.next.next 就会导致空指针异常
    if (temp != null && temp.next != null) {
        temp.next = temp.next.next;
    }
}

也可以创建一个变量记录当前遍历位置 location，用来判断到达的位置：

int location = 0;
while(true) {
	if(temp.next == null) { //已经到链表的最后
		break;
	}
	if ((index - 1) == location) {
	//找到的待删除节点的前一个节点 temp
		flag = true;
		break;
	}
	temp = temp.next; //temp 后移，遍历
}
//判断 flag
if(flag) { //找到
//可以删除
	temp.next = temp.next.next;
}else {
	System.out.printf("要删除的 %d 节点不存在\n", no);
	}
}

遍历链表

遍历数组的时候，可以用for循环遍历 a[ ] 中所有元素

for (int i = 0; i < N; i++) {
	// 处理a[i]
}

访问链表中是所有元素也有方法：索引变量x初始化为链表初节点，然后通过x.data访问与x相关联的元素，并将x设为x.next来访问链表下一个节点，直到x为null为止。

for (Node x = first; x != null; x = x.next) {
	// 处理x.data
}

其实也就是用一个辅助节点去依次走完整个链表，然后输出它的每次节点。

Node temp = head.next;   // 辅助节点，从首节点开始
//判断是否到链表最后
while (temp != null) {
    // 输出节点信息
    System.out.println(temp.data);
    // 后移，遍历下一个节点
    temp = temp.next;
}

修改节点的信息

这个不需要找到前一个节点，直接找到你要修改的那个节点，然后修改它的data即可。因为它对链表的结构链接没有影响

HeroNode temp = head.next; // 从第一个有效节点开始遍历

for (int i = 0; temp != null && i < index; i++) {
    temp = temp.next;
}

if (temp != null) {
    // 找到目标节点，进行修改
    temp.data = newData;
} else {
    // 目标节点不存在
    System.out.println("目标节点不存在");
}

单链表的相关操作：

1.求单链表中有效节点的个数：

定义一个计数器，再借助辅助节点从首节点开始遍历链表即可。

public static int getLength(Node head) {
    
	if(head.next == null) {
    	// 首节点为null，代表是空链表
    	return 0;
	}
	int length = 0;
	Node temp = head.next;
	while(temp != null) { 
		length++;
    	temp = temp.next; // 后移 
	}
	return length；
}

2.查找单链表中的倒数第 k 个结点:

? 因为单链表只能从前往后遍历，所有先遍历整个链表；确定这个链表的长度。然后通过总长度减去k就能知道它正数是第几个节点了；也就是它的正数索引值。

public static HeroNode findLastIndexNode(Node head, int index) {
	//判断如果链表为空，返回 null
	if(head.next == null) {
		return null;//没有找到
}
    //上一个问题已经求出了链表中的有效节点个数，也就是链表的长度了。
    int size = getLength(head);
    // 对 index 的值进行校验
    if(index <=0 || index > size) {
		return null;
	}
    // 从正向数的话，位置为 size-index
    // 定义辅助变量，让其找到倒数第 index 节点
    Node cur = head.next; 
	for(int i =0; i< size - index; i++) {
		cur = cur.next;
	}
	return cur;
}

3.单链表的反转（面试常出）：

? 单链表的反转，可以通过很多种方法实现。包括迭代法，递归法，

• 迭代法：

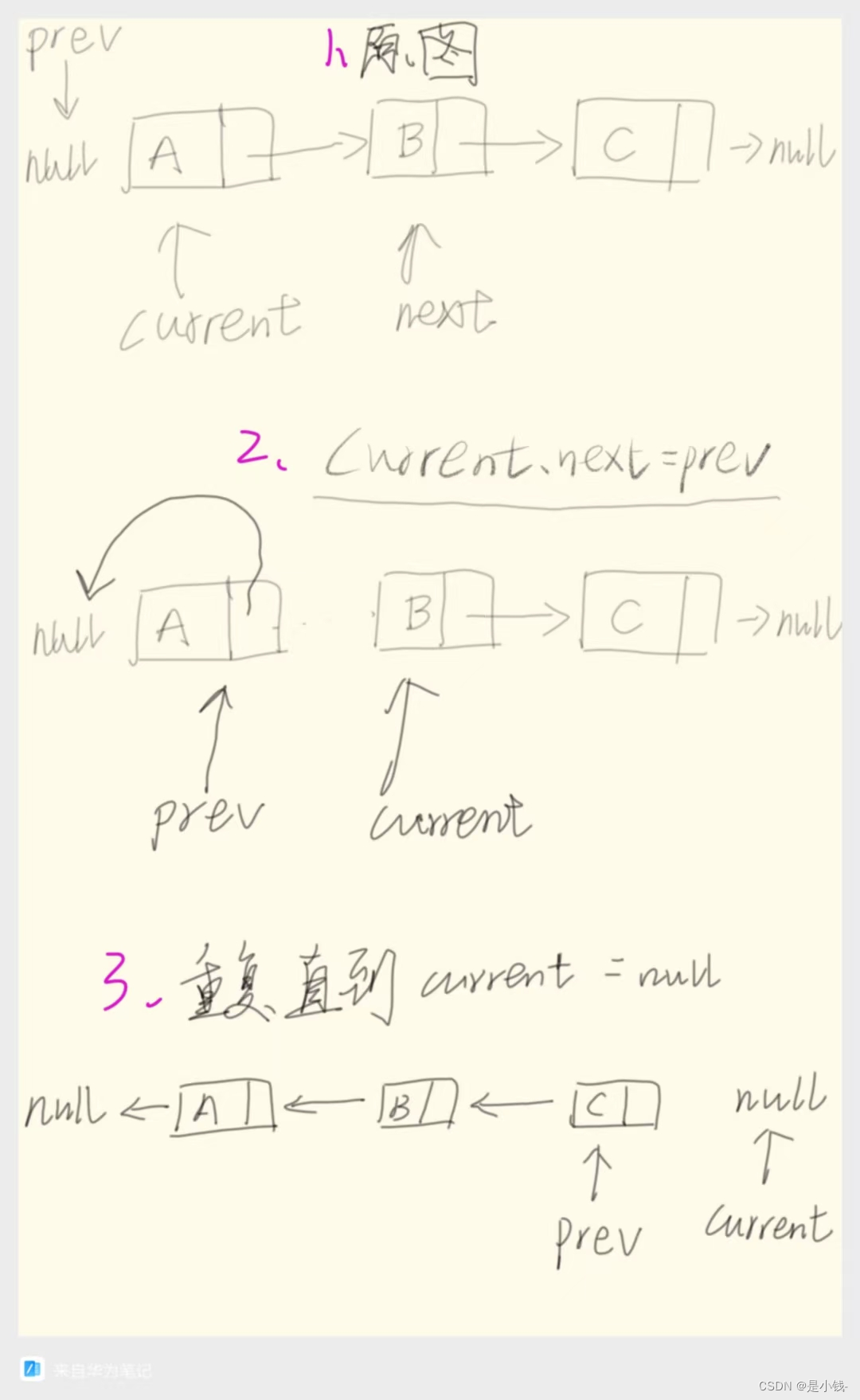
  1. 定义三个指针：prev、current和next，它们分别表示前一个节点、当前节点和下一个节点。

  2. 初始化时，prev为null，current为头节点。

  3. 在循环中，不断将current的next指针指向prev，然后依次向后移动prev、current和next指针。

  4. 当next为空时，说明已经到达链表末尾，此时的prev指向就是反转后的头节点。

  其实就像是先将第一个节点指向null，就像最后一个节点它也是next = null的；然后一直这样子重复，转一次就后退，让下一个节点去转方向指向前面的。

  

  public ListNode reverse(Node head) {
          Node prev = null;
          Node current = head;
  
          while (current != null) {
              Node nextTemp = current.next; // 暂存当前节点的下一个节点
              current.next = prev; // 将当前节点指向前一个节点
              prev = current; // 更新prev为当前节点
              current = nextTemp; // 更新current为原先的下一个节点
          }
  
          return prev; // 返回反转后的头节点
      }
  

  // 补充一个力扣第92题，加深理解（让你把单链表部分元素反转，其他部分不变）

• 

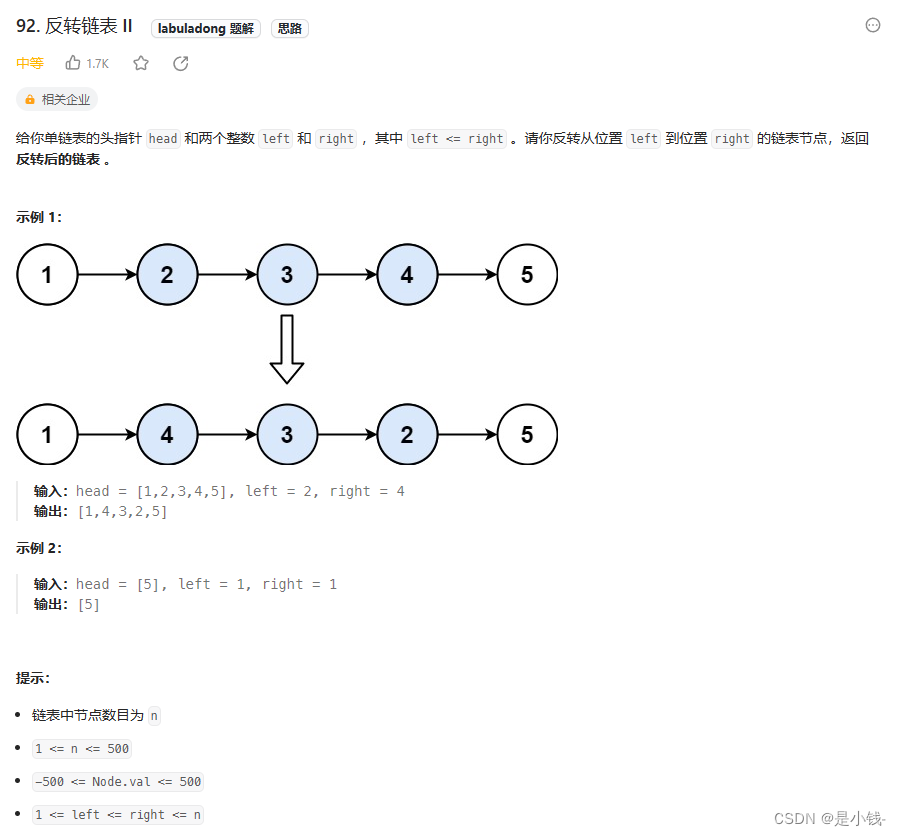
? 这里依旧可以使用迭代的方法，就是要先通过遍历去找到反转开始的位置和结束的位置；用辅助节点记录反转区间的前置节点和反转区间的尾节点。然后反转区间的链表反转即可，反转后接上前面的部分。

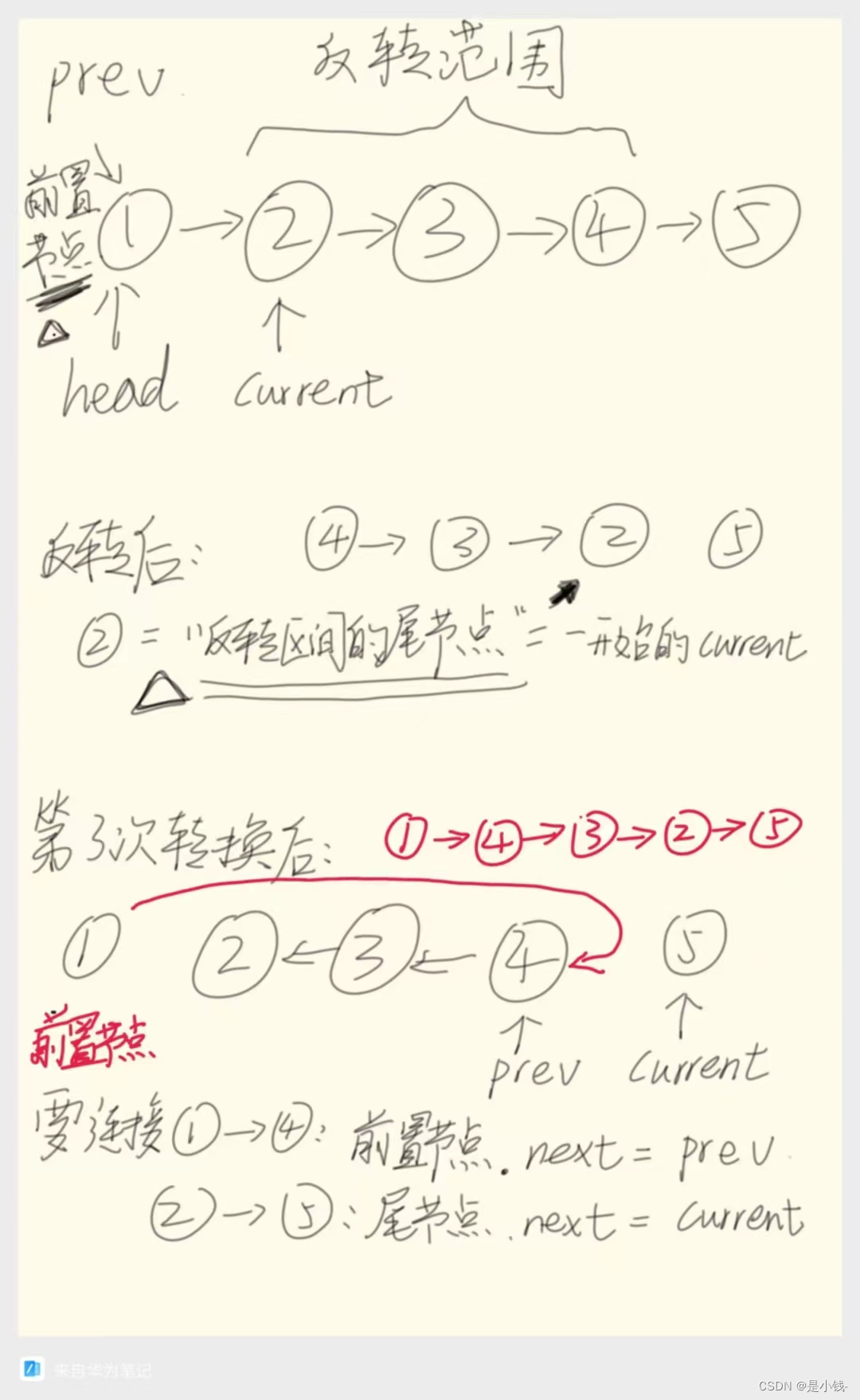
public ListNode reverseBetween(ListNode head, int left, int right) {
    ListNode current = head;
    ListNode prev = null;
    for (int i = 1; i < left; i++) {
        prev = current;
        current = current.next;
    }
    // 反转区间的前置节点
    ListNode tailPrev = prev;
    // 反转区间的尾节点
    ListNode tail = current;
    // 同样的迭代原理，只是范围要自定义。
    for (int j = left; j <= right; j++) {
        ListNode newTemp = current.next;
        current.next = prev;
        prev = current;
        current = newTemp;
    }
    // 反转区间的头节点
    ListNode headReverse = prev;
    tail.next = current;
    if (tailPrev != null) {
        tailPrev.next = headReverse;
        return head;
    } else {
        return headReverse;
    }
}

递归法：（也是力扣第206题）

? 递归的关键是看整体，找出整体的大块东西。可以先写一个伪代码过一遍思路。你就写基础情况，然后要的操作，再看子问题（递归调用）放的位置即可。

实操技巧：第一步先找到可以看作整体的，就是原理一样的。去设计递归调用（超级操作），第二步去设计微操作，去看一份整体的怎么实现即可。后面就去找到题目中的基础情况，它相当于最里面的超级操作了，也基本就是剩下一个的情况那种。

相关概念：

? 1.首先先明确函数的意义，还要原问题和子问题。在这里原问题是给整个链表反转，子问题是给每一个字节进行反转。

? 2.基础情况，也就是要找到结束的条件。就是当数据规模很小的时候，能结束递归，返回答案。

? 3.递归调用（超级操作），怎么搞定中间的递归操作。但是！唉！人脑进去递归出不来的。所以得完把递归的过程看成一个整体，不要去想里面怎么运行的。

? 4.微操作。也就是操作的方法。

? 比如汉诺塔问题，你有2个叠在一起的时候，就是先把小的放中间，大的放右边，再把小的放大的上面。那这个时候，假如他有一堆，你就是把小的一堆给放到中间，让最大的去到最右边垫底。然后小的一堆整体放到大的上面。而那一堆小的移动其实就是整个问题的子问题，它其实就是可以用递归重复一个原理完成。

此题思路如下：

想想只有2个怎么反转，那现在就把那一堆后面的看作一块。然后那一堆里面自己再反转就行，这就是它自己的超级操作咯，不理他。

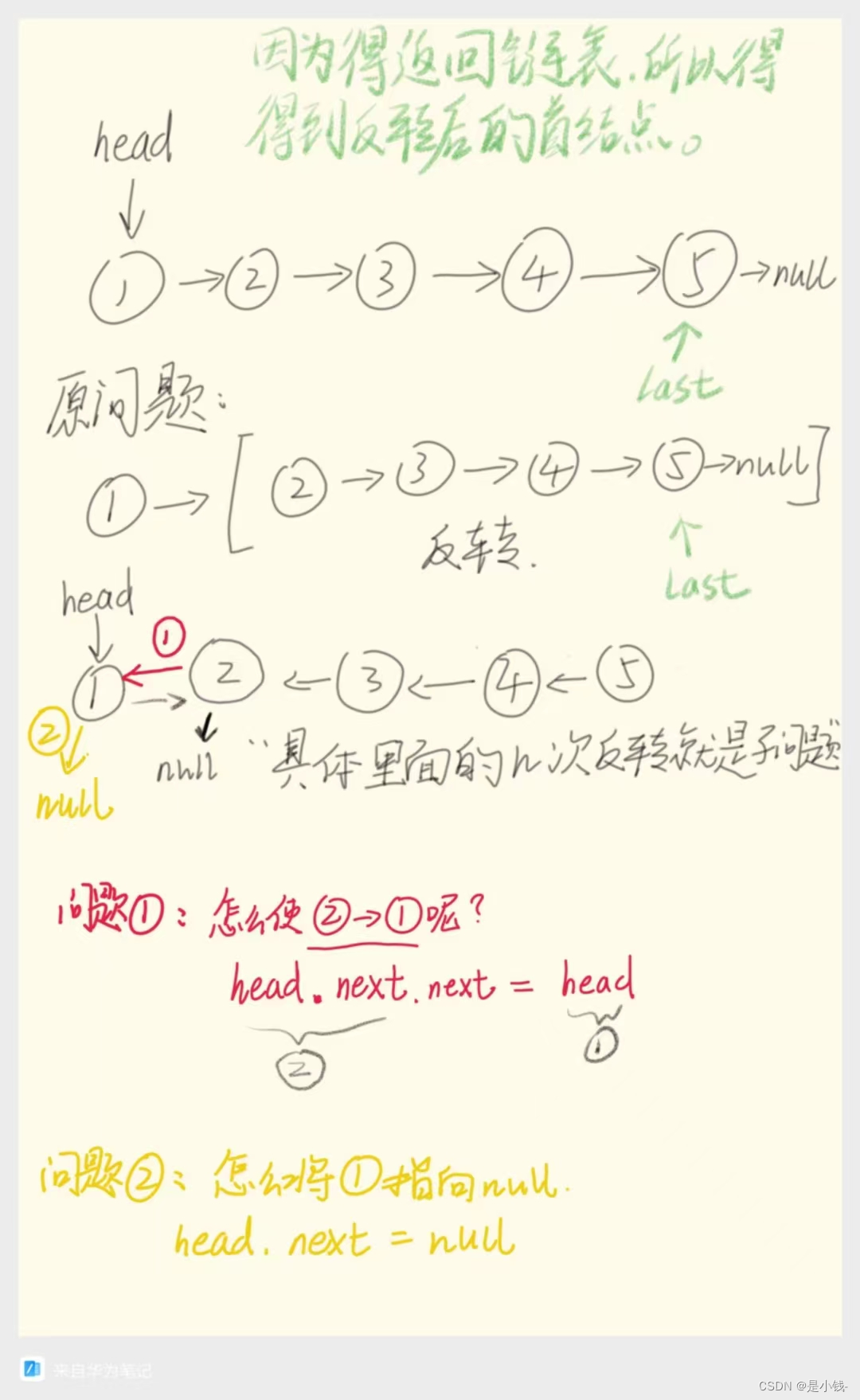
ListNode reverse(ListNode head) {
    // 基础情况，也就是结束的代码。
    // 链表为空或者只有一个节点时，直接返回头节点即可。
    if (head == null || head.next == null) {
        return head;
    }
    // 递归调用（超级操作）
    ListNode last = reverse(head.next);
    // 而其实当你写一个伪代码时候，你也可以发现。下面的这个其实就是反转需要的的操作，可以写一个伪代码，微操作。具体操作方法： operate(head.next); 
    head.next.next = head;
    head.next = null;
    return last;
}

再看看上面的力扣92题（反转部分链表）用递归法怎么做。

思路：其实他就是在整体反转改为一个范围内的反转，然后反转后，你要连接剩下的部分。所以你需要记录反转区间的两个点，即m-1和n+1这两个点。这个后面补

4.从尾到头打印单链表：

有两种方法：1.先进行反转，然后再遍历 （会破坏链表的原本顺序结构，不好）

? 2.利用栈的特性来实现。（先进后出）

public static void reversePrint(HeroNode head) {
	if(head.next == null) {
		return;//空链表，不能打印
	}
    //创建要给一个栈，将各个节点压入栈
	Stack<HeroNode> stack = new Stack<HeroNode>();
	HeroNode cur = head.next;
	//将链表的所有节点压入栈
	while(cur != null) {
		stack.push(cur);  // push 入栈
		cur = cur.next; //cur 后移，这样就可以压入下一个节点
	}
	//将栈中的节点进行打印,pop 出栈
	while (stack.size() > 0) {
		System.out.println(stack.pop()); 
	}
}

5.合并两个有序的单链表，合并之后的链表依然有序：

这里可以用到迭代的思路。迭代多用在：需要遍历；重复执行一段代码；直到满足要求。

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    // 创建一个值为 -1 的虚拟节点
	ListNode dummy = new ListNode(-1);
	ListNode current = dummy;

    // 依次遍历两个链表的节点，进行大小比较。
    // 此时两个链表都没有遍历完，进行大小比较入链表
	while (l1 != null && l2 != null) {
		if (l1.val <= l2.val) {
			current.next = l1;
            l1 = l1.next;
		} else {
            current.next = l2;
			l2 = l2.next;
		}
		current = current.next;
	}
    
	// 当某一个链表遍历完后，剩下的一条链表直接全部链接过去就行了
	if (l1 != null) {
		current.next = l1;
	} else {
        current.next = l2;
	}
    // 返回链表的头节点，因为dummy是虚拟节点。
	return dummy.next;
}

? 在 mergeTwoLists 方法中，我们使用 dummy 节点作为合并后链表的头节点。然后，我们使用 current 节点迭代合并两个链表。在循环中，比较两个链表当前节点的值，选择较小的节点连接到新链表上，并将对应链表的指针向后移动。最后，将剩余未处理完的链表连接到新链表的末尾。返回 dummy.next 即可得到合并后的有序链表。

双向链表

单链表的缺点：

• 查找只能单方向，双向链表有两个方向指向，所以可以从前往后或者从后往前。
• 删除和插入需要辅助节点，双向链表因为存在prev和next域，可以实现自我删除。

遍历：

? 和单链表方法一样，因为头节点不能动，使用辅助节点来遍历。正向的已经写过了，这里展示一个从后往前遍历的。先到尾节点，然后用prev域指向前一个节点依次遍历。

public void List(Node head) {
    Node current = head; // 当前节点
    
    // 将current指针移动到链表尾部
    while (current.next != null) {
        current = current.next;
    }
    
    // 从链表尾部向前遍历
    while (current != null) {
        System.out.println(current); // 打印当前节点的值
        current = current.prev; // 移动current指针到前一个节点
    }
}

添加节点：

? 指定位置的添加节点，你得知道要加在哪里。所以得用一个辅助节点去遍历找到位置，然后因为现在是双向链表了，添加逻辑就要修改一下了。

// 添加节点到链表尾部
public void add(Node node) {
	Node temp = head;
	while(true){
        // 到了链表的最后的话，就可以停下来了
        if(temp.next == null){
            break;
        }
        // 如果没有找到最后, 就将 temp 继续后移。让temp等于尾节点的位置
        temp = temp.next;
    }
    //添加逻辑： 尾节点.next = 要添加的; 要添加的.pre = temp;
    temp.next = node;
    node.pre = temp;
}

? 注意要先搞定新节点的指向问题！因为假如你先调整current节点的指向，那么等一下新节点就借助不了current来实现添加了！

	// 在指定索引位置插入节点
    public void insertAtIndex(int index, int data) {
        Node newNode = new Node(data);
        if (index < 0) {
            return;
        }
        // 新节点成为头节点
        if (index == 0) {
            newNode.next = head;
            // 链表为空的话，newNode.next将被赋值为null
            if (head != null) {
                head.prev = newNode;
            }
            // 让新节点成为头节点
            head = newNode;
            return;
        }
        // 让current到达插入点的位置
        Node current = head;
        int count = 0;
        while (count < index - 1 && current != null) {
            current = current.next;
            count++;
        }
        
        if (current == null) {
            System.out.println("大于链表的大小");
            return;
        }
	// 注意要先搞定新节点的指向！
    //因为假如你先调整current节点的指向，那么等一下新节点就借助不了current来添加。
       	// 新的节点指向下一个节点
        newNode.next = current.next;
        // 新的节点prev指回当前节点
        newNode.prev = current;
        // 代表已经是最后一个节点了，也就不需要下一个节点prev指回这个新节点的操作
        if (current.next != null) {
            // 下一个节点prev指回这个新节点
            current.next.prev = newNode;
        }
        // 当前节点指向新节点
        current.next = newNode;
    }

删除节点：

? 让temp去找到要删除的节点，这次不用找前一个节点了。有前后域，可以直接删除了。注意要先搞定新节点的指向问题！因为假如你先调整current节点的指向，那么等一下新节点就借助不了current来添加。

	// 在指定索引位置删除节点
    public void deleteAtIndex(int index) {
        if (head == null || index < 0) {
            System.out.println("空链表或者删除的位置不存在");
            return;
        }

        if (index == 0) {
            head = head.next;
            if (head != null) {
                head.prev = null;
            }
            return;
        }

        Node current = head;
        int count = 0;
        while (count < index && current != null) {
            current = current.next;
            count++;
        }
		// 这个index已经超过了链表范围了
        if (current == null) {
            return;
        }
		// 判断是否到最后一个节点了，下面两个代码顺序对于删除操作是没有影响的
        if (current.next != null) {
            current.next.prev = current.prev;
        }
        current.prev.next = current.next;
    }

修改节点元素实现和单链表这个一样的，也利用不到双向链表的性质。

单向环形链表（约瑟夫环问题）

? Josephu 问题为：设编号为 1，2，… n 的 n 个人围坐一圈，约定编号为 k（1<=k<=n）的人从 1 开始报数，数到 m 的那个人出列，它的下一位又从 1 开始报数，数到 m 的那个人又出列，依次类推，直到所有人出列为止，由此 产生一个出队编号的序列。

分析与思路：

1. 先构建一个n个节点的单向环形链表
2. 从k节点开始，从1计到m，就输出和删除那个m的节点。
3. 然后下一个节点又从1开始这样循环下去，全部删除完就结束。

创建环形链表

? 尾节点指回头节点就行了，一开始的节点也要指向自身。

public class CircularLinkedList {
    private Node head;

    // 节点类
    private static class Node {
        int data;
        Node next;

        public Node(int data) {
            this.data = data;
            this.next = null;
        }
    }

	// 在链表末尾插入节点
    public void insert(int data) {
        Node newNode = new Node(data);
        if (head == null) {
            head = newNode;
            head.next = head; // 将头节点的 next 指针指向自身，形成环
        } else {
            Node current = head;
            // 判断当前节点的下一个节点是否等于头节点
            // 循环链表，最后一个节点是指向头节点的
            while (current.next != head) {
                current = current.next;
            }
            // 将最后一个节点指向新节点
            current.next = newNode;
            // 新节点的 next 指针指向头节点，形成环
            newNode.next = head; 
        }
    }
    
    // 遍历链表
    public void printList() {
        if (head == null) {
            return;
        }
        Node current = head;
        while (true) {
            // 要先打印首节点，因为可能链表就一个节点。
            // 假如先判断，这样子首节点指向自己，停止循环。则不打印首节点了
            System.out.printf(current.data);
			if (current.next == head) { // 说明已经遍历完毕
				break;
			}
			current = current.next; 
        }
    }

出圈思路如图分析：

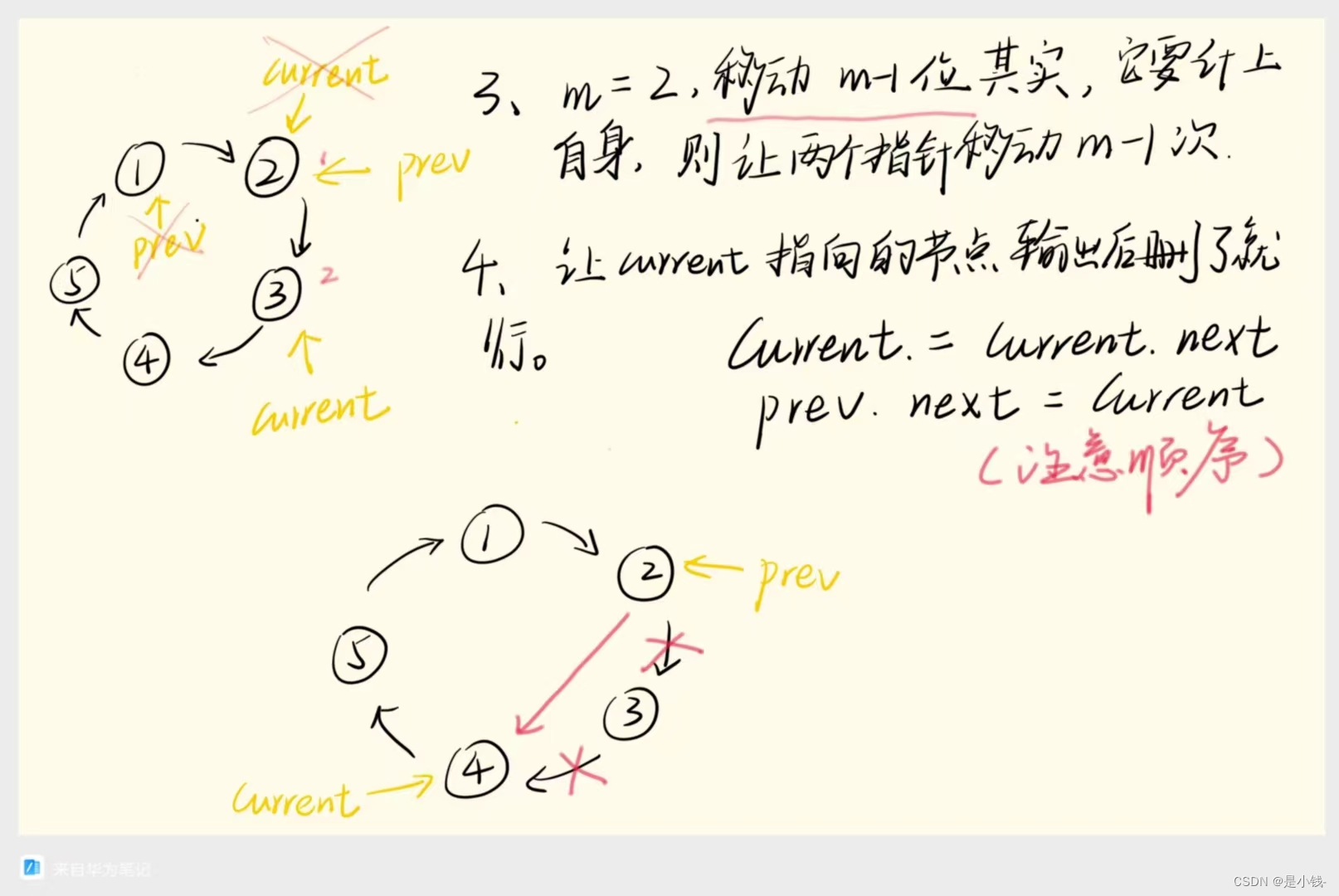
• 优化：这里可以把prev设计成null，则省了遍历整个链表去找最后一个节点的过程，将当前节点移动到开始出圈的位置，只用把prev = current即可。

其实这个就是一个双指针问题，双指针问题解决链表问题很常见。后续会出相关的专题

代码：

public void josephus(int k, int m, int n) {
        if (head == null || k <= 0 || m <= 0 || n <= 0) {
            return;
        }

        Node current = head;
    	// 这里设计成null，则省了遍历整个链表去找最后一个节点的过程
        Node prev = null;

        // 将当前节点移动到开始出圈的位置
        for (int i = 0; i < k - 1; i++) {
            prev = current;
            current = current.next;
        }

        // 开始模拟出圈过程
        while (current.next != current) {
            for (int i = 0; i < m - 1; i++) {
                // 继续移动到要删除的节点
                prev = current;
                current = current.next;
            }
            prev.next = current.next;
            System.out.print(current.data + " ");
            current = prev.next;
        }
    	// 最后留在里面的节点
        System.out.println(current.data);
    }
}

链表有一些力扣题目，这个后面再结合力扣刷题来写。