头歌—衍生密码体制

# 第1关：Rabin密码体制

题目描述

---

任务描述

Rabin密码体制是RSA密码体制的一种。 本关任务：使用Rabin密码体制对给定的明文进行加密。

相关知识

为了完成本关任务，你需要掌握：Rabin密码体制。

Rabin密码体制

在本关中，我们描述Rabin密码体制，假定模数n=pq不能被分解，则该类体质对于选择明文攻击是计算安全的。因此Rabin密码体制提供了一个可证明安全的密码体制的例子：假定分解整数问题是计算上不可行的，Rabin密码体制是安全的，我们现在来描述Rabin密码体制。

Rabin密码体制：设n=pq，其中p和q为素数，且p,q≡3(mod4)。设P=C=Zn?，且定义：K=(n,p,q)。 对于K=(n,p,q)，定义 eK(x)=x²mod n 和dK(y)=(y)mod n，其中n的值为公钥，p和q为私钥。

Rabin密码体制的一个缺点是加密函数并不是一个单射，所以解密不能以一种明显的方式完成。我们证明如下。假定y是一个有效的密文，这意味着y=x2mod n，对于某一`x∈Z_n^?。

让我们从Bob的观点来看解密问题。它得到一个密文y，且想找出 x 使得

x²≡y(mod n)

这是一个关于Zn中未知元x的二次方程，解密需要求出模n的平方根。这等价于求解两个同余方程：

z²≡y(mod p)和z²≡y(mod q)

我们可以利用欧拉准则，来判断y是否为一个模p的二次剩余。实际上如果加密正确地执行，则y是一个模p和模q的二次剩余。不幸的是，欧拉准则并不能帮我们找到y的平方根，他仅能得到一个“是”或“否”的答案。

当p≡3(mod 4)时，有一个简单公式来计算模p二次剩余的平方根。假定y是一个模p二次剩余，且p≡3(mod 4)，那么我们有:

(±y^(p+1)/4)²≡y^(p+1)/2(mod p)

≡y^(p?1)/2y(mod p)

≡y(mod p)

这里我们又一次使用了欧拉准则，即如果y是一个模p二次剩余，那么`y^(p?1)/2≡1(mod p)

因此，y 模 p 的两个平方根为

±y^(p+1)/4(mod p)。

同样的讨论，可知 y 模 p 的两个平方根为

±y^(q+1)/4(mod q)，

然后可以直接用中国剩余定理来得到y模n的四个平方根。

例： 我们用一个小例子来说明Rabin密码体制的加密和解密过程，假定n=77=7×11。那么加密函数为：

e_K(x)=x²mod 77

且解密函数为：

d_K(y)=y^1/2mod 77

假定Bob需要解密密文y=23。首先需要找到23模7和模11的平方根。由于7和11都是模4余3，我们利用前面的公式：

23(7+1)/4≡22≡4(mod 7)` `23(11+1)/4≡13≡1(mod 11)

利用中国剩余定理，我们计算23模77的四个平方根为±10,±32mod 77。因此，四个可能的明文为x=10,32,45,67。可以验证这四个明文平方后模77，约化得到的值为23。这证明了23是一个有效的秘文。

编程要求

根据提示，补全右侧编辑器中 Begin-End 区间的代码，给定模数n和明文x，要求使用Rabin密码体制进行加密。具体要求如下：

• 从后台获取两个数字n和x，输出加密后的密文。

测试说明

平台会对你编写的代码进行测试：

测试输入：

84773093 84754668

预期输出：

8887 9539

思路

看到了这段：

顺手试了一下就成了，没往深了想。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll  long  long
ll e(ll x, ll n);
int main()
{
    int n,x;
    cin>>n>>x;

	printf("%lld", e(x, n));

    return 0;
}

ll e(ll x, ll n) {
	return (x*x) % n;
}

第2关：RSA的语义安全

题目描述

任务描述

前面所说的所有攻破密码体制，实际上是试图找出秘密密钥(对称密码体制的情形)或者私钥(公钥密码体制的情形)。然而，可能敌手的目标并没有那么大的野心，即不能找到秘密密钥或者私钥，他仍可以获得比我们所希望的更多的信息，如果要确保一个密码体制是“安全”的，我们应该考虑这些敌手所具有的适度的目标。

本关任务：给定h表和n的值，利用二分搜索求解出明文。

相关知识

为了完成本关任务，你需要掌握：RSA的语义安全。

RSA的语义安全

到现在为止，我们假定敌手试图攻破密码体制以找出秘密密钥。如果Oscar能够做到这一点，那么密码体制被完全攻破。然而，可能敌手的目标并没有这么大的野心。即使Oscar不能找到秘密密钥或公钥，他仍然可以获得比我们所希望的更多的信息。如果我们要确保一个密码体制是“安全的”，我们应该更准确的估计敌手的目的。 下面列出了潜在的敌手的目的。

完全攻破 敌手能够找出Bob的秘密密钥或者私钥。因此他能解密利用给定密钥加密的任意密文。

部分攻破 敌手能以某一不可忽略的概率解密之前没有见过的密文。或者，敌手能够对于给定的密文，得出明文的一些特定信息。

密文识别 敌手能够以超过1/2的概率识别两个不同明文对应的密文或者识别出给定明文的秘文和随机字符串。

在下面的内容中，我们考虑一些针对RSA类密码体制达到上面某种类型目的可能攻击。我们也介绍在一定的计算假设成立的情形下，如何构造一个公钥密码体制使得敌手不能在多项式时间内识别密文，这样的密码体制称为达到了语义安全。达到语义安全是非常困难的，因为我们是在对抗敌手非常弱的、容易达到目的的攻击。

一些密码体制的弱点就是明文的部分信息可以通过密文“泄露”出去。这表示是对系统的一种部分攻破，实际上它在RSA密码体制中发生了。假定我们给定密文，

y=x^bmod n,

其中x表示明文。由于gcd(b,?(n))=1，必然是 b 为奇数的情形。因此 jacobi 符号为

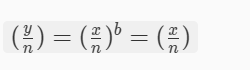
所以，给定密文y，任何人无需解密密文就可以有效地计算(nx)。也就是说，一个RSA加密“泄露”了一些有关明文的信息，即Jacobi符号(nx)的值。

在本关中，我们考虑一些由密码体制泄露的其他特定类型的部分信息:

1.给定y=eK(x)，计算parity(y)，其中parity(y)表示x的二进制表示的最低位数。 2.给定y=eK(x)，计算half(y)，其中0≤x≤n/2时，half(y)=0；当n/2<x≤n?1时，half(y)=1。

我们将证明假定RSA加密是安全的，RSA密码体制不会泄露这种类型的信息。更精确的说，我们将证明RSA密码解密问题可以Turing约化为计算half(y)的问题。这意味着如果存在一个多项式算法计算half(y)，那么存在RSA解密的多项式时间算法。也就是说，计算关于明文的特定信息，即half(y)，不会比解密密文得到整个明文来得容易。

我们现在讨论，在给定计算half(y)的假设算法的前提下，如何计算y=dK(x)，算法如下所示。

我们对算法的原理做一下解释。首先，我们注意到RSA加密函数满足在Zn中的如下乘法性质: eK(x1)eK(x2)=eK(x1x2)

现在利用如下事实: y=eK(x)=xbmod n

容易看到，对于0≤i≤?log2n? ,第一个for循环运行第i次时有： hi=half(y×(eK(2))i)==half(eK(x×2i))

我们观察到

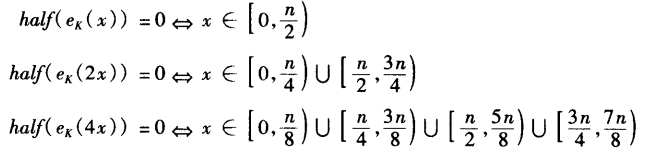
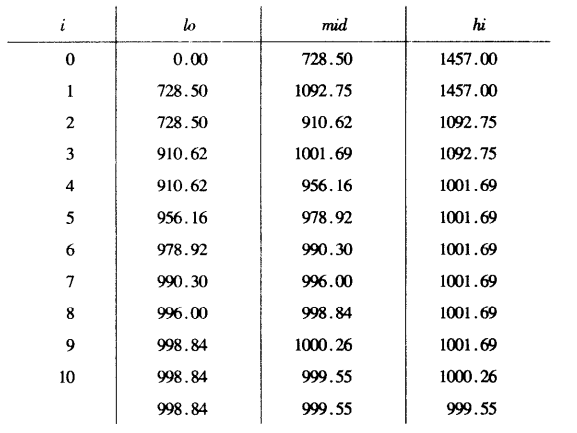
等等，因此我们利用二分检索技巧来找到x，这就是第二个for循环中完成的。下面用一个小例子来说明。 例 假定n=1457,b=779，且我们有一个密文y=722。然后假定，我们利用预言Half，我们得到如下hi值：

然后我们利用二分查索过程，如下表所示，因此明文为y=?999.55?=999。

编程要求

根据提示，补全右侧编辑器中 Begin-End 区间的代码，给定h表和n的值，利用二分搜索求解出明文。具体要求如下：

• 从后台获取一个字符串

  h
  

  和一个整数

  n
  

  ，利用二分搜索求解明文并输出。

  测试说明

平台会对你编写的代码进行测试：

测试输入：

10101111100
1457

预期输出：

999

思路

字符串是h表，题目已经给出了，我们只需要二分查找y的值即可，向下取整。

过程就是下面这个图，共二分h次，h=1时，l = mid，h=0，r = mid

代码

#include<bits/stdc++.h>
using namespace std;
#define ll  long  long
char h[100];

int main()
{
    int n;
    scanf("%s",h);
    scanf("%d",&n);

	int len = strlen(h);

	double l = 0, r = n, mid = 0;

	for (int i = 0; i < len; i++) {
		mid = l + (r - l) / 2;
		if (h[i] == '1') l = mid;
		else r = mid;
	}

	cout << int(floor(mid));
    return 0;
}