线性回归模型数值仿真
发布时间:2023年12月23日
设y=hθ(x)=a+bx+??是一个直线方程,其中𝜀 是高斯噪声。请采100个输入样本,计算出相应的输出样本,并利用线性回归模型拟合这些样本,利用最小二乘求解。可视化这两类算法的回归的结果
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
np.random.seed(42)
# 1. 生成100个输入样本
x = np.random.rand(100, 1) * 10 # 随机生成在0-10范围内的100个数
# 2. 根据方程 y = a + bx + epsilon 计算输出
# 生日: 12月
a = 2
b = 1
epsilon = np.random.randn(100, 1) # 生成高斯噪声
y = a + b*x + epsilon
# 3. 使用线性回归模型拟合这些样本
reg = LinearRegression().fit(x, y)
# 4. 获取拟合的参数
a_hat = reg.intercept_[0]
b_hat = reg.coef_[0][0]
# 5. 可视化原始数据和回归结果
plt.scatter(x, y, color='blue', label='Original Data with Noise')
plt.plot(x, reg.predict(x), color='red', label=f'Fitted Line: y = {a_hat:.2f} + {b_hat:.2f}x')
plt.title("Linear Regression Result")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()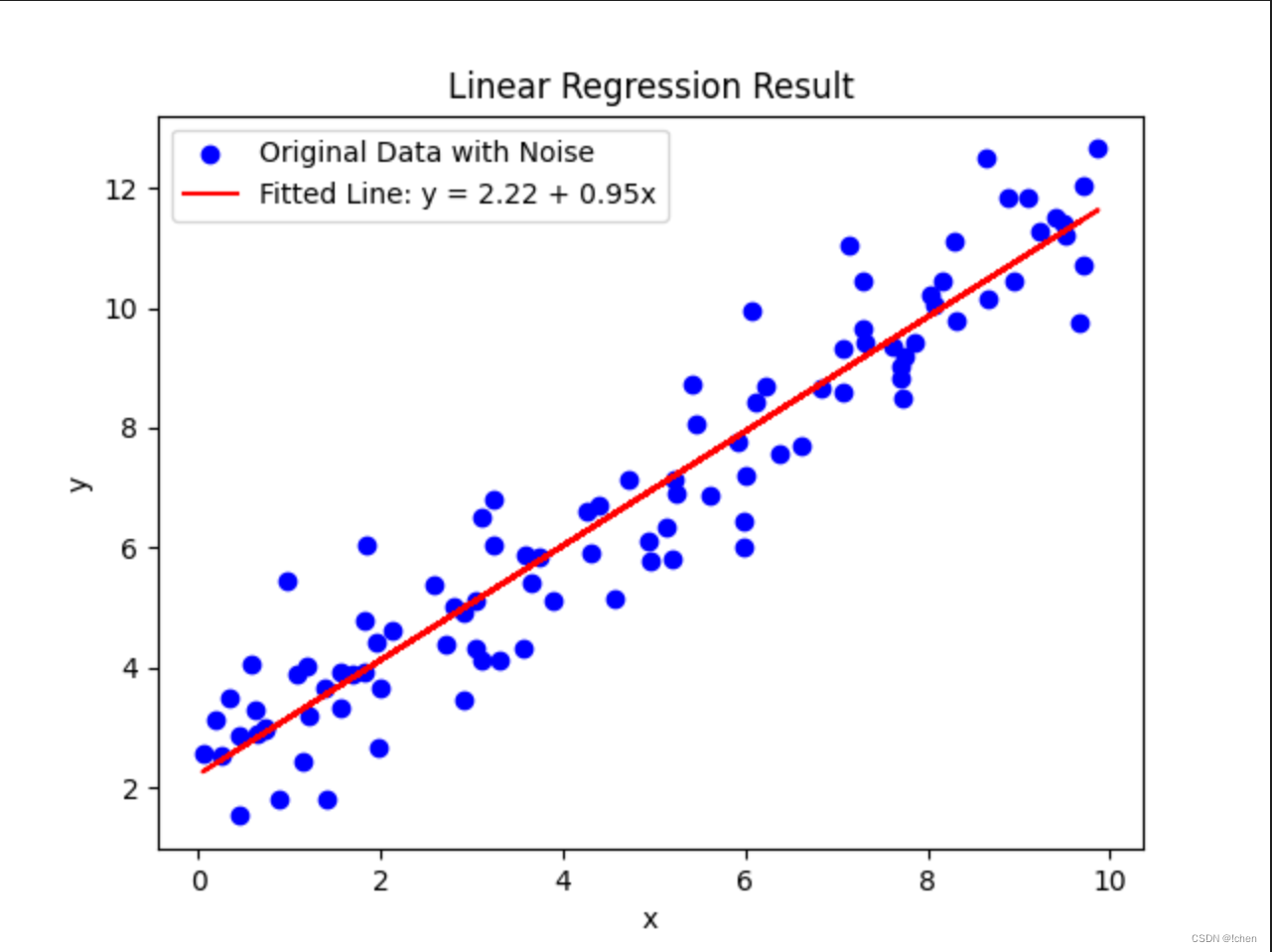
文章来源:https://blog.csdn.net/xdpcxq/article/details/135172759
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- NTP8835(30W+2X10W 2.1音箱专用D类功放IC)
- Maven高级篇
- jsoncpp学习
- quic协议及核心源码分析
- 腾讯云轻量2核2G3M应用服务器62元一年,阿里云63元选哪个?
- PayPal账户被封是因为什么?如何解决?
- 大数据人工智能在线实习项目:某实习网站招聘信息采集与分析
- Ai创建一个文档
- scrapy_redis原理分析并实现断点续爬以及分布式爬虫
- 【数据结构】哈希表详解,举例说明 java中的 HashMap