每日一练：LeeCode-111. 二叉树的最小深度【二叉树】

本文是力扣LeeCode-111. 二叉树的最小深度 学习与理解过程，本文仅做学习之用，对本题感兴趣的小伙伴可以出门左拐LeeCode。

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

示例 1：

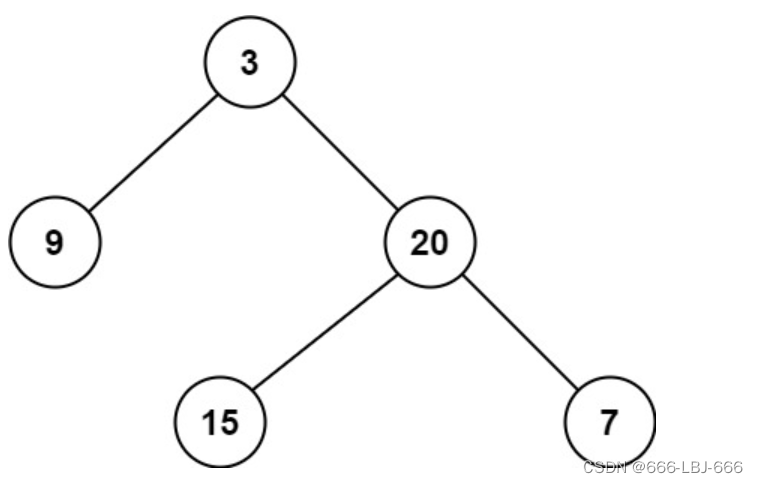
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

思路

这道题的思路和二叉树的最大深度的几乎一样，都是通过后序遍历的方式求解,，但是区别在于对叶子结点的判断上。叶子节点是指没有子节点的节点，即：叶子结点没有右左右孩子节点

递归法

• 确定递归函数的参数和返回值: int getDepth(TreeNode node)
• 确定终?条件: if(node==null)return 0;
• 确定单层递归的逻辑:
  最大深度中的单层代码逻辑

        int leftHeight = getDepth(node.left);	//左
        int rightHeight = getDepth(node.right);	//右
        int height = 1+Math.max(leftHeight,rightHeight);	//中
        return height;

此处和最大深度中的单层代码逻辑不太一样，需要考虑根节点一边节点为空的情况，因为这种情况会影响叶子结点的判断，最小深度应为1 + 根节点左/右?树的深度 。所以代码中需要额外考虑：1、当?个左?树为空，右?树不为空； 2、当?个右?树为空，左?树不为空

        int leftHeight = getDepth(node.left);	// 左
        int rightHeight = getDepth(node.right);// 右
		// 当?个左?树为空，右不为空，这时并不是最低点
        if(node.left==null&&node.right!=null){	// 中
            return 1+rightHeight;
        }
        // 当?个右?树为空，左不为空，这时并不是最低点
        if(node.left!=null&&node.right==null){
            return 1+leftHeight;
        }

        int height = 1+Math.min(leftHeight,rightHeight);
        return height;

代码实现

class Solution {
    public int minDepth(TreeNode root) {
        return getDepth(root);
    }

    private int getDepth(TreeNode node){
        if(node==null)return 0;
        int leftHeight = getDepth(node.left);	// 左
        int rightHeight = getDepth(node.right);// 右
		// 当?个左?树为空，右不为空，这时并不是最低点
        if(node.left==null&&node.right!=null){	// 中
            return 1+rightHeight;
        }
        // 当?个右?树为空，左不为空，这时并不是最低点
        if(node.left!=null&&node.right==null){
            return 1+leftHeight;
        }

        int height = 1+Math.min(leftHeight,rightHeight);
        return height;
    }
}

最终要的一句话：做二叉树的题目，首先需要确认的是遍历顺序

大佬们有更好的方法，请不吝赐教，谢谢