状态压缩dp模型整理

状态压缩dp的核心在于将每一层视为一个状态，这些状态用二进制来表示，每一层由上一层转移而来，那么这么来看的话，我们只用预处理本层的每一个状态可以由上一层的哪些状态转移而来，然后由此来更新本层每个状态即可。这种一般由于状态不能选满，所以看似时间复杂度很高，但实际循环跑不满。

我们结合实际的例子来看一下这种题比较套路的解法：

基于连通的状态压缩dp

1064. 小国王（活动 - AcWing）

思路：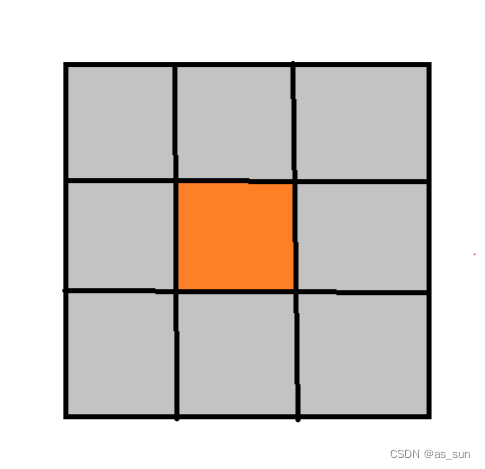

如图，在中间格子放上一个国王之后，周围八个位置都不能再放了，由于我们这里划分是一层一层划分的，所以本层是由上一层转移而来，那么先只看相邻的两行，那就是图1，然后我们保证每行行内是有效的，那就是2,3,4，然后我们就可以据此找出行与行之间可以成立的条件。

总结一下就是满足三个个条件：

1.每行内部不能有两个相邻的

2.两行之间对应位置求&结果是0

3.两行之间对应位置求异或，得到的结果也不能有两个相邻位置都是1

会发现1和3都要判断二进制数的相邻位置的情况，所以我们可以单独写一个函数来实现。

然后整体思路就是，我们先预处理出来每行可以放的合法方案，然后再预处理一下每个状态可以由哪些状态转移而来。

定义dp[i][j][a]为已经填完i行，用了j个国王，第i行的状态为a

据此dp[i-1][j-count(a)][b]则为已经填完i-1行，用了j-count(a)个国王，第i-1行的状态为b

很显然dp[i][j][a]可以由dp[i-1][j-count(a)][b]转移而来，而dp[i-1][j-count(a)][b]的前两维都确定了，只有第三维是不定的，第三维的所有合法情况都累加到dp[i][j][a]，则为dp[i][j][a]的结果。那么就是判断状态a和b是否可以共存的问题。如果可以就能累加，否则就不行。而经过预处理后，我们可以直接枚举可以使用的b，进一步优化。最后为了再优化一下，不然就要循环a的值来找结果，我们直接计算到dp[n+1][m][0],那么第n层的所有方案都可以累加给它，直接输出这个值即可。另外记得给初态赋值，dp[0][0][0]=1，因为一个都不选也是一种方案。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[12][120][1<<10];
vector<int>sta;
vector<int>h[1<<10];
int n,m;

bool check(int s)
{
    for(int i=0;i<n;i++)
    {
        if((s>>i&1) && (s>>i+1&1)) return false;
    }
    return true;
}

int count(int x)
{
    int ans=0;
    for(int i=0;i<n;i++) ans += x>>i&1;
        //if(x>>i&1) ans++;
    return ans;
}

int cnt[1<<10];
int main()
{
    
    scanf("%d%d",&n,&m);//n是行数和列数
    for(int i=0 ; i<1<<n ; i++)
    {
        if(check(i)) 
        {
            sta.push_back(i);
            cnt[i]=count(i);
        }
    }
    

    for(int i=0;i<sta.size();i++)
    {
        for(int j=0;j<sta.size();j++)
        {
            int a=sta[i],b=sta[j];
            if(a&b) continue;
            if(check(a|b)) h[i].push_back(j);
        }
    }
    
    dp[0][0][0]=1;//
    for(int i=1;i<=n+1;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<sta.size();k++)
            {
                for(auto it:h[k])
                {
                    int a=sta[k],b=sta[it];
                    if(j>=cnt[a])dp[i][j][a]+=dp[i-1][j-cnt[a]][b];
                }
            }
        }
    }
    cout<<dp[n+1][m][0];
}

327. 玉米田（327. 玉米田 - AcWing题库）?

思路：这里还是一行一行种，所以我们要看每行内部以及行与行之间的合法情况。

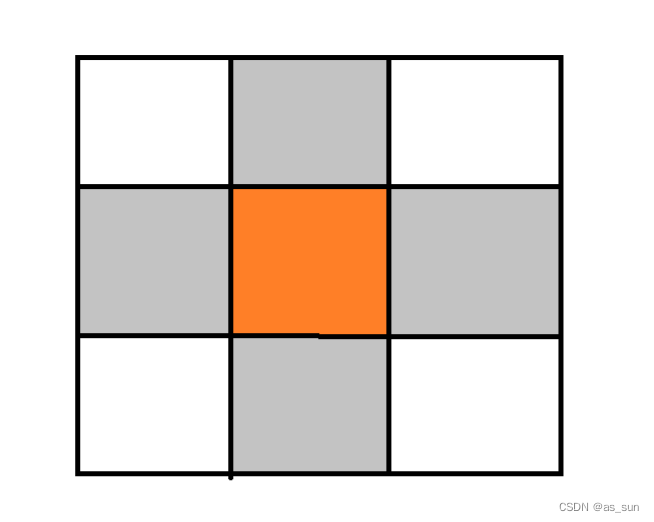
这个画出来就很清楚了，而且比上一种实际简单一点，因为每行内部考虑一下，然后行与行之间只要取&结果不为1即可。

那么就类似上面的思路，先将合法的状态预处理出来，再将合法转移预处理出来，然后推出来的表达式更新每一层每个状态时的值，而且由于这里没有数量上限，比上面还少一维。不过这里有一点要注意，每一行中有些地方不能种，那么其实我们也可以用把土地状况转化成一个二进制的数，然后在计算的时候与我们选择的状态取&来判断是否合法，如果合法再转移。

定义dp[i][a]表示填完第i行且第i行的状态为a时，能种的最大玉米数

dp[i-1][b]为填完i-1行且第i-1行状态为b时，能种的最大玉米数，

g[i]表示第i行的土地状态，如果不能种则对应的二进制位为1

if(!(a&g[i]))dp[i][a]+=dp[i-1][b]),枚举a,b(b可以直接用预处理出来的值)

也同上面一样，我们多处理一行，输出dp[n+1][0]的值

另外因为求和，所以需要对dp[0][0]预处理，dp[0][0]=1;

#include<bits/stdc++.h>
using namespace std;
const int M=1<<12;
vector<int>h[M];
vector<int>sta;
int g[20],dp[20][M];
int n,m;
const int mod=1e8;
int check(int sta)
{
    for(int i=0;i<m;i++)
    {
        if((sta>>i&1) && (sta>>i+1&1)) return 0;
    }
    return 1;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<m;j++)//二进制从第0位开始
        {
            int c;
            scanf("%d",&c);
            if(!c) g[i] += (1<<j); 
        }
    }
    for(int i=0;i < 1<<m;i++)
    {
        if(check(i))
        {
            sta.push_back(i);
        }
    }
    for(int i=0;i<sta.size();i++)
    {
        for(int j=0;j<sta.size();j++)
        {
            int a=sta[i],b=sta[j];
            if(a&b) continue;
            h[i].push_back(j);
        }
    }
    dp[0][0]=1;
    for(int i=1;i<=n+1;i++)
    {
        for(int j=0;j<sta.size();j++)
        {
            for(auto it:h[j])
            {
                int a=sta[j],b=sta[it];
                if(!(g[i]&a)) dp[i][a] = (dp[i][a]+dp[i-1][b])%mod;
            }
        }
    }
    cout<<dp[n+1][0];
}

?292. 炮兵阵地(292. 炮兵阵地 - AcWing题库)

这个题很像上面两个题的综合，或是说玉米田的进阶版，因为它的范围扩大了，我们不能只考虑上一行，需要考虑前两行，另外有些地方不能放。对于不能放的位置的处理和玉米田的处理一样，关键在于前两行这个转移该怎么看。

这里再引入一种集合定义方式，dp[i][a][b]表示填完第i行，第i-1行的状态为a,第i行的状态为b的情况。

那么它可以由什么转移而来呢，很显然是dp[i-1][c][b],只要a,b,c三者关系是合法的即可。

合法即(a&b)|(a&c)|(b&c) != 1

那么实际上就可以写了，我们只需要预处理每一行即可。??

而且我们注意到这里是求最多能放多少个，c有很多个状态，但我们实际上只能取使结果最大的一种，而且我们要注意到我们实际是用下标来表示状态的，而不是直接用a,b,c

因为我们求的不是方案数，所以不能相加。

#include<bits/stdc++.h>
using namespace std;
const int M=1<<10;
vector<int>sta;
int g[120];
int dp[2][M][M];
int n,m;
int cnt[M];
int check(int sta)
{
    for(int i=0;i<m;i++)
    {
        if( (sta>>i&1) && ( (sta>>i+1&1)||(sta>>i+2&1) ) ) return 0;
    }
    return 1;
}
int count(int x)
{
    int ans=0;
    for(int i=0;i<m;i++) ans+= (x>>i)&1;
    return ans;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        string s;
        cin>>s;
        for(int j=0;j<m;j++)
        {
            if(s[j]=='H') g[i] += 1<<j;
        }
    }
    
    for(int i=0;i< 1<<m;i++)
        if(check(i))
        {    
            sta.push_back(i);
            cnt[i]=count(i);
        }   
    for(int i=1;i<=n;i++)
    {
        for(int x=0;x<sta.size();x++)//i
        {
            for(int y=0;y<sta.size();y++)//i-1
            {
                for(int z=0;z<sta.size();z++)//i-2
                {
                    int a=sta[x],b=sta[y],c=sta[z];
                    if(a&b | b&c | a&c ) continue;
                    if(g[i]&a | g[i-1]&b) continue;
                    dp[i&1][y][x]=max(dp[i&1][y][x],dp[i-1&1][z][y]+cnt[a]);
                }
            }
        }
    }
    int ans=0;
    for(int x=0;x<sta.size();x++)//i
    {
        for(int y=0;y<sta.size();y++)//i-1
        {
            ans = max(ans,dp[n&1][x][y]);
        }
    }
    cout<<ans;
}

基于集合的状态压缩dp

524. 愤怒的小鸟（524. 愤怒的小鸟 - AcWing题库）

思路：我们先来理解下题目的意思，在平面直角坐标系的第一象限有若干个点，我们要用尽可能少的过原点且开口向下的抛物线去覆盖它们，问最少需要多少条。

所以首先我们要将所有有效的抛物线算出来，根据抛物线的式子，可以发现两点就能算出来一条抛物线，所以总共有n*n条抛物线。然后算出来的抛物线可能不仅仅经过这两个点，还能经过其他点，所以我们固定两个点，去计算经过它们的抛物线可以经过哪些点，作为状态记录下来。

然后我们用第i位上的0或者1表示第i个点有没有选上。那么状态就从0->111...1(n个1，转成十进制数就是2^n-1)。

这里我们定义dp[i]表示当前n个点的状态，然后从中找到一个没有被覆盖的点，然后去找经过这个点的抛物线，通过那条抛物线的状态得到当前的状态。然后去更新。?

#include<bits/stdc++.h>
using namespace std;
#define x first 
#define y second
typedef pair<double,double> pdd;
pdd q[20];//如果定义vector<pdd>记得清空
const int N=1<<18;
int f[N];
int p[20][20];
const double eps=1e-8;
int cmp(double a,double b)
{
    if(fabs(a-b)<eps) return 0;
    if(a<b) return -1;
    else return 1;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=0;i<n;i++) 
        {
            double x,y;
            scanf("%lf%lf",&x,&y);
            q[i].x=x,q[i].y=y;
        }
        memset(p,0,sizeof p);
        for(int i=0;i<n;i++)
        {
            p[i][i]=1<<i;
            for(int j=0;j<n;j++)
            {
                double x1=q[i].x,y1=q[i].y;
                double x2=q[j].x,y2=q[j].y;
                if(!cmp(x1,x2)) continue;
                double a=(y1/x1-y2/x2)/(x1-x2);
                double b=y1/x1-a*x1;
                if(cmp(a,0)>=0) continue;
                int s=0;
                for(int k=0;k<n;k++)
                {
                    double x=q[k].x,y=q[k].y;
                    if(!cmp(a*x*x+b*x,y))
                        s += 1<<k;
                }
                p[i][j]=s;
            }
        }
        memset(f,0x3f,sizeof f);
        f[0]=0;
        for(int i=0;i+1 < 1<<n;i++)//11..11不用循环
        {
            int x=0;
            for(int j=0;j<n;j++)
                if(!(i>>j&1))
                {
                    x=j;
                    break;
                }

            for(int j=0;j<n;j++)
                f[i|p[x][j]]=min(f[i]+1,f[i|p[x][j]]);
        }
        cout<<f[(1<<n)-1]<<endl;
    }
}

ps:另外这里有一点要注意，因为浮点数储存可能会出现误差，所以判断等于不等需要加上容错?

?