数据结构——二叉树的操作
发布时间：2024年01月07日
一、实验目的（本次实验所涉及并要求掌握的知识点）
?????? 1.领会二又链存储结构;掌握二又树的各种基本运算和构造二叉树的算法设计。
?????? 2.领六线索二又树的构造过程以及构造线索二又树的算法设计。
二、实验内容与设计思想（设计思路、主要数据结构、主要代码结构、主要代码段分析）
1. 实验内容
2. 抽象数据类型定义
ADT Tree
{
数据对象：
??? D = {ai | 1 <= i <= n, n >= 0,ai 为ElemType类型}
数据关系：
??? R = {<ai,aj> | ai,aj∈D,1 <= i,j <= n,其中有且仅有一个节点没有前驱节点，其余每一个节点只有一个前驱节点，但可以有零个或多个后继节点}
基本运算：
TreeNode * createBinaryTree(); // 创建二叉树的二叉链存储结构
void freeBinaryTree(TreeNode* root); // 释放二叉树的内存
int getHeight(TreeNode* root); // 获取树的高度
void printParenthesisTree(TreeNode* root); // 输出二叉树的括号表示法
void printIndentedTree(TreeNode* root, int level); // 输出二叉树的凹入表示法
void printChildNodes(TreeNode* root, char target); // 输出结点的左、右孩子结点值
void preorderTraversal(TreeNode* root); // 先序遍历二叉树
void inorderTraversal(TreeNode* root); // 中序遍历二叉树
TreeNode* constructTree(char* preorder, char* inorder, int len); // 构造二叉树（根据先序序列和中序序列）
void inorderThreading(TreeNode* root, TreeNode** prev); // 中序线索化二叉树
void inorderThreadedTraversal(TreeNode* root); // 非递归方式遍历输出中序线索二叉树的中序序列
void postorderTraversal(TreeNode* root); // 后序遍历二叉树
}
3. 设计思路
- 数据结构设计：
- 定义二叉树结点的数据结构 TreeNode，包含数据域 data、左孩子指针 left、右孩子指针 right，以及左右孩子标志 ltag 和 rtag。
- ltag 和 rtag 用于线索化二叉树时标记结点的左右孩子指针是否为实际孩子（0表示实际孩子，1表示前驱/后继线索）。
- 二叉树的创建：
- 先依次开辟内存
- 直接用指针逐个指定他们的左右孩子值
- 二叉树的释放：
- 使用递归方式实现 freeBinaryTree 函数，先释放左子树，再释放右子树，最后释放根结点的内存空间。
- 二叉树的高度计算：
- 使用递归方式实现 getHeight 函数，计算左子树和右子树的高度，并返回较大值加1作为树的高度。
- 二叉树的括号表示法输出：
- 使用递归方式实现 printParenthesisTree 函数，先输出当前结点的数据域，再判断是否有子树。
- 如果存在左子树或右子树，则在括号内递归输出左子树和右子树。
- 二叉树的凹入表示法输出：
- 使用递归方式实现 printIndentedTree 函数，根据当前层级的值，输出对应数量的空格，然后输出当前结点的数据域，并换行。
- 递归输出左子树和右子树时，层级加1。
- 结点的左右孩子结点输出：
- 使用递归方式实现 printChildNodes 函数，在遍历过程中，如果当前结点的数据域与目标值相等，输出左孩子和右孩子的值。
- 二叉树的先序、中序、后序遍历：
- 使用递归方式实现 preorderTraversal、inorderTraversal 和 postorderTraversal 函数，按照先序、中序和后序遍历的顺序递归输出结点的值。
- 先序、中序构造二叉树：
- 使用递归方式实现 constructTree 函数，根据给定的先序序列和中序序列构造二叉树。
- 先序序列中的第一个结点为根结点，在中序序列中找到该结点的位置，将中序序列分为左子树和右子树部分。
- 递归构造根结点的左子树和右子树，返回根结点。
- 中序线索化二叉树：
- 使用递归方式实现 inorderThreading 函数，中序遍历二叉树并进行线索化。
- 在中序遍历过程中，对于每个结点，判断其左孩子是否为空，如果为空，则将左孩子指针指向前驱结点，并设置线索标志。
- 如果前驱结点的右孩子为空，则将右孩子指针指向当前结点，并设置线索标志。
- 非递归方式遍历输出中序线索二叉树的中序序列：
- 使用非递归方式实现 inorderThreadedTraversal 函数，根据线索化的信息进行中序遍历。
- 从根结点开始，沿着左子树一直找到第一个被线索化的结点，输出其数据域。
- 如果该结点有右线索，移动到右孩子结点；否则，沿着右子树一直找到下一个被线索化的结点。
- 主菜单和选项处理：
- 在主函数 main 中，通过一个循环显示菜单，并根据用户选择的选项执行相应的操作。
- 每个选项对应一个函数调用，根据二叉树是否存在进行相应的操作或输出提示信息。
4. 数据结构定义
// 二叉树结点的定义
typedef struct TreeNode {
char data; // 结点数据
struct TreeNode* left; // 左孩子结点指针
struct TreeNode* right; // 右孩子结点指针
int ltag; // 左线索标志，0表示左子结点指向左孩子，1表示左子结点指向前驱
int rtag; // 右线索标志，0表示右子结点指向右孩子，1表示右子结点指向后继
} TreeNode;
TreeNode* createBinaryTree(); // 创建二叉树的二叉链存储结构
void freeBinaryTree(TreeNode* root); // 释放二叉树的内存
int getHeight(TreeNode* root); // 获取树的高度
void printParenthesisTree(TreeNode* root); // 输出二叉树的括号表示法
void printIndentedTree(TreeNode* root, int level); // 输出二叉树的凹入表示法
void printChildNodes(TreeNode* root, char target); // 输出结点的左、右孩子结点值
void preorderTraversal(TreeNode* root); // 先序遍历二叉树
void inorderTraversal(TreeNode* root); // 中序遍历二叉树
TreeNode* constructTree(char* preorder, char* inorder, int len); // 构造二叉树（根据先序序列和中序序列）
void inorderThreading(TreeNode* root, TreeNode** prev); // 中序线索化二叉树
void inorderThreadedTraversal(TreeNode* root); // 非递归方式遍历输出中序线索二叉树的中序序列
void postorderTraversal(TreeNode* root); // 后序遍历二叉树
5. 程序中各函数调用关系
1、createBinaryTree 函数：用于创建二叉树，根据给定的先序字符串和中序字符串构造二叉树的节点，返回根节点指针。
2、printChildNodes 函数：用于输出指定结点的左右孩子结点的值，接收二叉树的根节点指针和目标结点值作为参数。
3、getHeight 函数：?用于计算二叉树的高度，接收二叉树的根节点指针作为参数，返回树的高度。
4、printIndentedTree 函数：用于以凹入表示法输出二叉树，接收二叉树的根节点指针和层级作为参数。
5、printParenthesisTree 函数：用于以括号表示法输出二叉树，接收二叉树的根节点指针作为参数。
6、preorderTraversal 函数：用于先序遍历二叉树，接收二叉树的根节点指针作为参数。
7、inorderTraversal 函数：用于中序遍历二叉树，接收二叉树的根节点指针作为参数。
8、postorderTraversal 函数：用于后序遍历二叉树，接收二叉树的根节点指针作为参数。
9、freeBinaryTree 函数：用于释放二叉树的内存空间，接收二叉树的根节点指针作为参数。
10、constructTree 函数：用于根据给定的先序序列和中序序列构造二叉树，接收先序序列、中序序列和序列长度作为参数，返回根节点指针。
11、inorderThreading 函数：用于中序线索化二叉树，将二叉树中的结点进行线索化，接收二叉树的根节点指针和前驱结点指针的指针作为参数。
12、inorderThreadedTraversal 函数：用于非递归方式遍历输出中序线索化二叉树的中序序列，接收二叉树的根节点指针作为参数。
这些函数之间的调用关系如下：
- constructTree 函数内部会调用 createBinaryTree 函数来构建二叉树。
- constructTree 函数在构建完二叉树后，会调用 inorderThreading 函数对二叉树进行中序线索化。
- inorderThreadedTraversal 函数在遍历输出中序线索化二叉树的中序序列时，会调用 inorderThreading 函数来获取前驱结点。
其他函数之间没有直接的调用关系。
三、实验使用环境（本次实验所使用的平台和相关软件）??
Visual stdio
四、实验步骤和调试过程（实验步骤、测试数据设计、测试结果分析）
1. 测试数据
----------------------------------------------
二叉树的操作
----------------------------------------------
主菜单
1.创建二叉链存储结构 b
2.输出‘H’结点的左、右孩子结点
3.输出二叉树 b的高度
4.凹入表示法输出二叉树 b
5.括号表示法输出二叉树 b
6.先序遍历二叉树
7.中序遍历二叉树
8.后序遍历二叉树
9.释放二叉树
10.先序、中序构造二叉树 b
11.退出
-----------------------------------------------
请输入选项（1~11）：
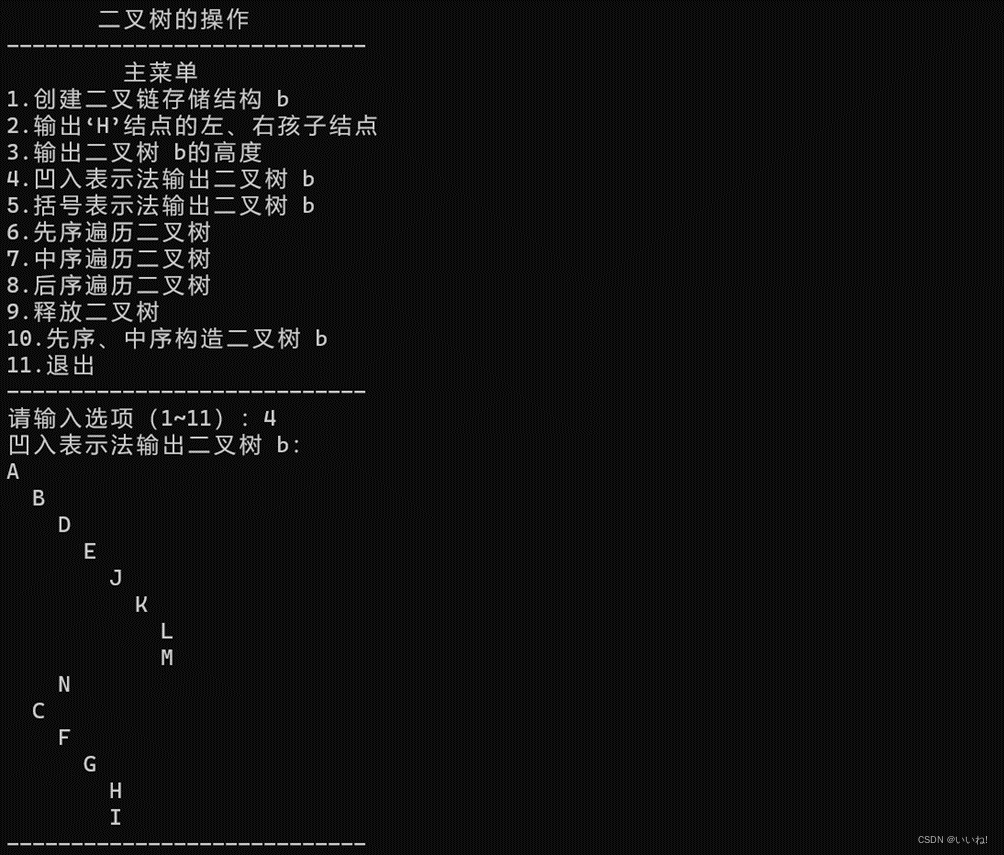
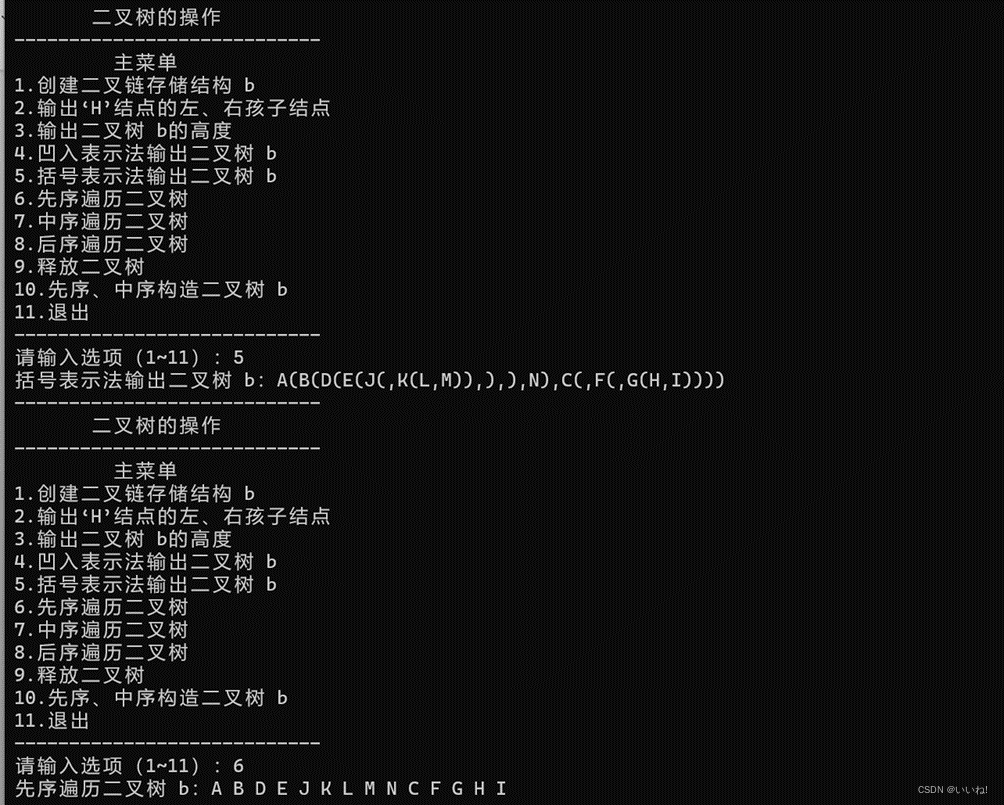
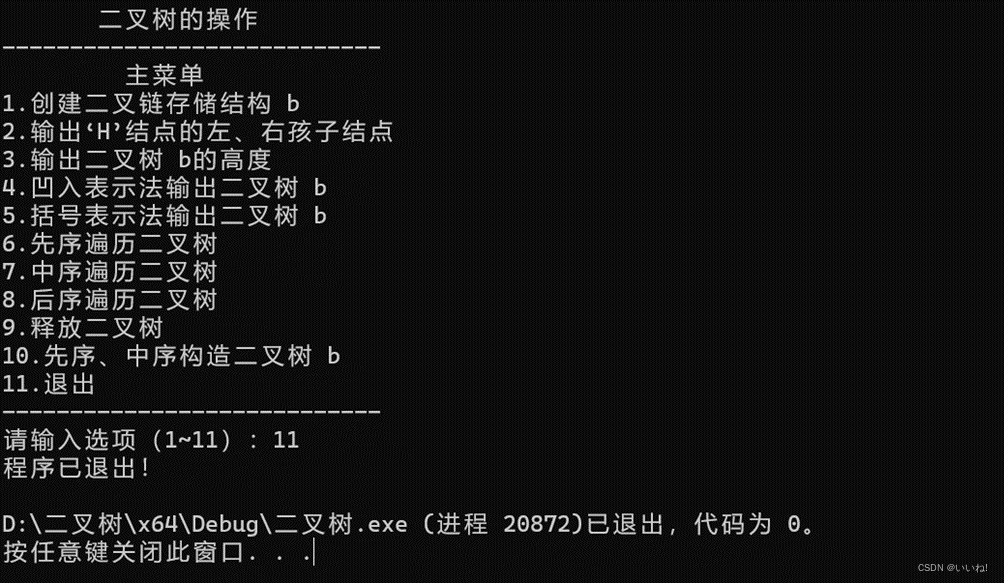
2. 程序运行结果截图
先序、中序构造二叉树之后：
五、附录代码
//btree.h
// 二叉树结点的定义
typedef struct TreeNode {
char data; // 结点数据
struct TreeNode* left; // 左孩子结点指针
struct TreeNode* right; // 右孩子结点指针
int ltag; // 左线索标志，0表示左子结点指向左孩子，1表示左子结点指向前驱
int rtag; // 右线索标志，0表示右子结点指向右孩子，1表示右子结点指向后继
} TreeNode;
TreeNode* createBinaryTree(); // 创建二叉树的二叉链存储结构
void freeBinaryTree(TreeNode* root); // 释放二叉树的内存
int getHeight(TreeNode* root); // 获取树的高度
void printParenthesisTree(TreeNode* root); // 输出二叉树的括号表示法
void printIndentedTree(TreeNode* root, int level); // 输出二叉树的凹入表示法
void printChildNodes(TreeNode* root, char target); // 输出结点的左、右孩子结点值
void preorderTraversal(TreeNode* root); // 先序遍历二叉树
void inorderTraversal(TreeNode* root); // 中序遍历二叉树
TreeNode* constructTree(char* preorder, char* inorder, int len); // 构造二叉树（根据先序序列和中序序列）
void inorderThreading(TreeNode* root, TreeNode** prev); // 中序线索化二叉树
void inorderThreadedTraversal(TreeNode* root); // 非递归方式遍历输出中序线索二叉树的中序序列
void postorderTraversal(TreeNode* root); // 后序遍历二叉树//btree.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "btree.h"
// 创建二叉树的二叉链存储结构
TreeNode* createBinaryTree() {
TreeNode* A = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* B = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* C = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* D = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* E = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* F = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* G = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* H = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* I = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* J = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* K = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* L = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* M = (TreeNode*)malloc(sizeof(TreeNode));
TreeNode* N = (TreeNode*)malloc(sizeof(TreeNode));
A->data = 'A';
B->data = 'B';
C->data = 'C';
D->data = 'D';
E->data = 'E';
F->data = 'F';
G->data = 'G';
H->data = 'H';
I->data = 'I';
J->data = 'J';
K->data = 'K';
L->data = 'L';
M->data = 'M';
N->data = 'N';
A->left = B;
A->right = C;
B->left = D;
B->right = E;
C->left = F;
C->right = G;
D->left = NULL;
D->right = NULL;
E->left = H;
E->right = NULL;
F->left = NULL;
F->right = NULL;
G->left = NULL;
G->right = I;
H->left = J;
H->right = K;
I->left = NULL;
I->right = NULL;
J->left = NULL;
J->right = NULL;
K->left = L;
K->right = M;
L->left = NULL;
L->right = NULL;
M->left = NULL;
M->right = N;
N->left = NULL;
N->right = NULL;
return A;
}
// 释放二叉树的内存
void freeBinaryTree(TreeNode* root) {
if (root == NULL) {
return;
}
freeBinaryTree(root->left);
freeBinaryTree(root->right);
free(root);
}
// 获取树的高度
int getHeight(TreeNode* root) {
if (root == NULL) {
return 0;
}
int leftHeight = getHeight(root->left);
int rightHeight = getHeight(root->right);
return (leftHeight > rightHeight) ? (leftHeight + 1) : (rightHeight + 1);
}
// 输出二叉树的括号表示法
void printParenthesisTree(TreeNode* root) {
if (root == NULL) {
return;
}
printf("%c", root->data);
if (root->left != NULL || root->right != NULL) {
printf("(");
printParenthesisTree(root->left);
printf(",");
printParenthesisTree(root->right);
printf(")");
}
}
// 输出二叉树的凹入表示法
void printIndentedTree(TreeNode* root, int level) {
if (root == NULL) {
return;
}
for (int i = 0; i < level; i++) {
printf(" ");
}
printf("%c\n", root->data);
printIndentedTree(root->left, level + 1);
printIndentedTree(root->right, level + 1);
}
// 输出结点的左、右孩子结点值
void printChildNodes(TreeNode* root, char target) {
if (root == NULL) {
return;
}
if (root->data == target) {
if (root->left != NULL) {
printf("左孩子：%c\n", root->left->data);
}
else {
printf("左孩子：无\n");
}
if (root->right != NULL) {
printf("右孩子：%c\n", root->right->data);
}
else {
printf("右孩子：无\n");
}
}
printChildNodes(root->left, target);
printChildNodes(root->right, target);
}
// 先序遍历二叉树
void preorderTraversal(TreeNode* root) {
if (root == NULL) {
return;
}
printf("%c ", root->data);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
// 中序遍历二叉树
void inorderTraversal(TreeNode* root) {
if (root == NULL) {
return;
}
inorderTraversal(root->left);
printf("%c ", root->data);
inorderTraversal(root->right);
}
// 后序遍历二叉树
void postorderTraversal(TreeNode* root) {
if (root == NULL) {
return;
}
postorderTraversal(root->left);
postorderTraversal(root->right);
printf("%c ", root->data);
}
// 构造二叉树（根据先序序列和中序序列）
TreeNode* constructTree(char* preorder, char* inorder, int len) {
if (len == 0) {
return NULL;
}
TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
root->data = preorder[0];
root->ltag = 0;
root->rtag = 0;
int rootIndex = 0;
for (int i = 0; i < len; i++) {
if (inorder[i] == root->data) {
rootIndex = i;
break;
}
}
root->left = constructTree(preorder + 1, inorder, rootIndex);
root->right = constructTree(preorder + rootIndex + 1, inorder + rootIndex + 1, len - rootIndex - 1);
if (root->left != NULL) {
root->ltag = 1;
}
if (root->right != NULL) {
root->rtag = 1;
}
return root;
}
// 中序线索化二叉树
void inorderThreading(TreeNode* root, TreeNode** prev) {
if (root == NULL) {
return;
}
inorderThreading(root->left, prev);
if (root->left == NULL) {
root->left = *prev;
root->ltag = 1;
}
if (*prev != NULL && (*prev)->right == NULL) {
(*prev)->right = root;
(*prev)->rtag = 1;
}
*prev = root;
inorderThreading(root->right, prev);
}
// 非递归方式遍历输出中序线索二叉树的中序序列
void inorderThreadedTraversal(TreeNode* root) {
if (root == NULL) {
return;
}
TreeNode* p = root;
while (p->ltag == 0) {
p = p->left;
}
while (p != NULL) {
printf("%c ", p->data);
if (p->rtag == 1) {
p = p->right;
}
else {
p = p->right;
while (p != NULL && p->ltag == 0) {
p = p->left;
}
}
}
}//main.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "btree.h"
int main() {
TreeNode* b = NULL;
int option;
char str[] = "A(B(D,E(H(J,K(L,M(,N))))),C(F,G(,I)))";
do {
printf("----------------------------\n");
printf(" 二叉树的操作\n");
printf("----------------------------\n");
printf(" 主菜单\n");
printf("1.创建二叉链存储结构 b\n");
printf("2.输出‘H’结点的左、右孩子结点\n");
printf("3.输出二叉树 b的高度\n");
printf("4.凹入表示法输出二叉树 b\n");
printf("5.括号表示法输出二叉树 b\n");
printf("6.先序遍历二叉树\n");
printf("7.中序遍历二叉树\n");
printf("8.后序遍历二叉树\n");
printf("9.释放二叉树\n");
printf("10.先序、中序构造二叉树 b\n");
printf("11.退出\n");
printf("----------------------------\n");
printf("请输入选项（1~11）：");
scanf("%d", &option);
switch (option) {
case 1:
if (b != NULL) {
printf("二叉树 b 已存在，请先释放再创建！\n");
}
else {
int index = 0;
b = createBinaryTree(str, &index);
printf("二叉树 b 创建成功！\n");
}
break;
case 2:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
printChildNodes(b, 'H');
}
break;
case 3:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
int height = getHeight(b);
printf("二叉树 b 的高度：%d\n", height);
}
break;
case 4:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
printf("凹入表示法输出二叉树 b：\n");
printIndentedTree(b, 0);
}
break;
case 5:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
printf("括号表示法输出二叉树 b：");
printParenthesisTree(b);
printf("\n");
}
break;
case 6:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
printf("先序遍历二叉树 b：");
preorderTraversal(b);
printf("\n");
}
break;
case 7:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
printf("中序遍历二叉树 b：");
inorderTraversal(b);
printf("\n");
}
break;
case 8:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
printf("后序遍历二叉树 b：");
postorderTraversal(b);
printf("\n");
}
break;
case 9:
if (b == NULL) {
printf("二叉树 b 不存在，请先创建！\n");
}
else {
freeBinaryTree(b);
b = NULL;
printf("二叉树 b 释放成功！\n");
}
break;
case 10:
if (b != NULL) {
printf("二叉树 b 已存在，请先释放再创建！\n");
}
else {
char preorder[] = "ABDEJKLMNCFGHI";
char inorder[] = "JLKMEDBNACFIGH";
int len = strlen(preorder);
b = constructTree(preorder, inorder, len);
printf("先序、中序构造二叉树 b 完成！\n");
}
break;
case 11:
printf("程序已退出！\n");
break;
default:
printf("无效的选项，请重新输入！\n");
break;
}
} while (option != 11);
return 0;
}
文章来源:https://blog.csdn.net/m0_73059486/article/details/135424922
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Edge扩展插件安装位置
- [云原生] Go 定时器
- 分类预测 | Matlab实现WOA(海象)-XGboost分类【24年新算法】基于海象优化算法(WOA)优化XGBoost的数据分类预测
- JavaScript 本地存储
- 企业微信开发：自建应用：接收消息（企业内部服务器）/回调配置
- java:解决SPI机制遇到的非典型问题-ServiceLoad.load(Class＜T＞ service)方法失效
- redis数据结构（二）—— 对象
- 什么是有机搜索引擎优化以及如何入门
- django工资管理系统(程序+开题)
- 分享5款简单实用的软件，值得收藏