Unity中Shader矩阵变换的几何体现

---

前言

我们在这篇文章中，了解一下矩阵的几何意义。

---

一、点 的 向量表达形式 和 矩阵表达形式

我们在图形计算器中，形象的看一下，这两种表达方式之间的关系

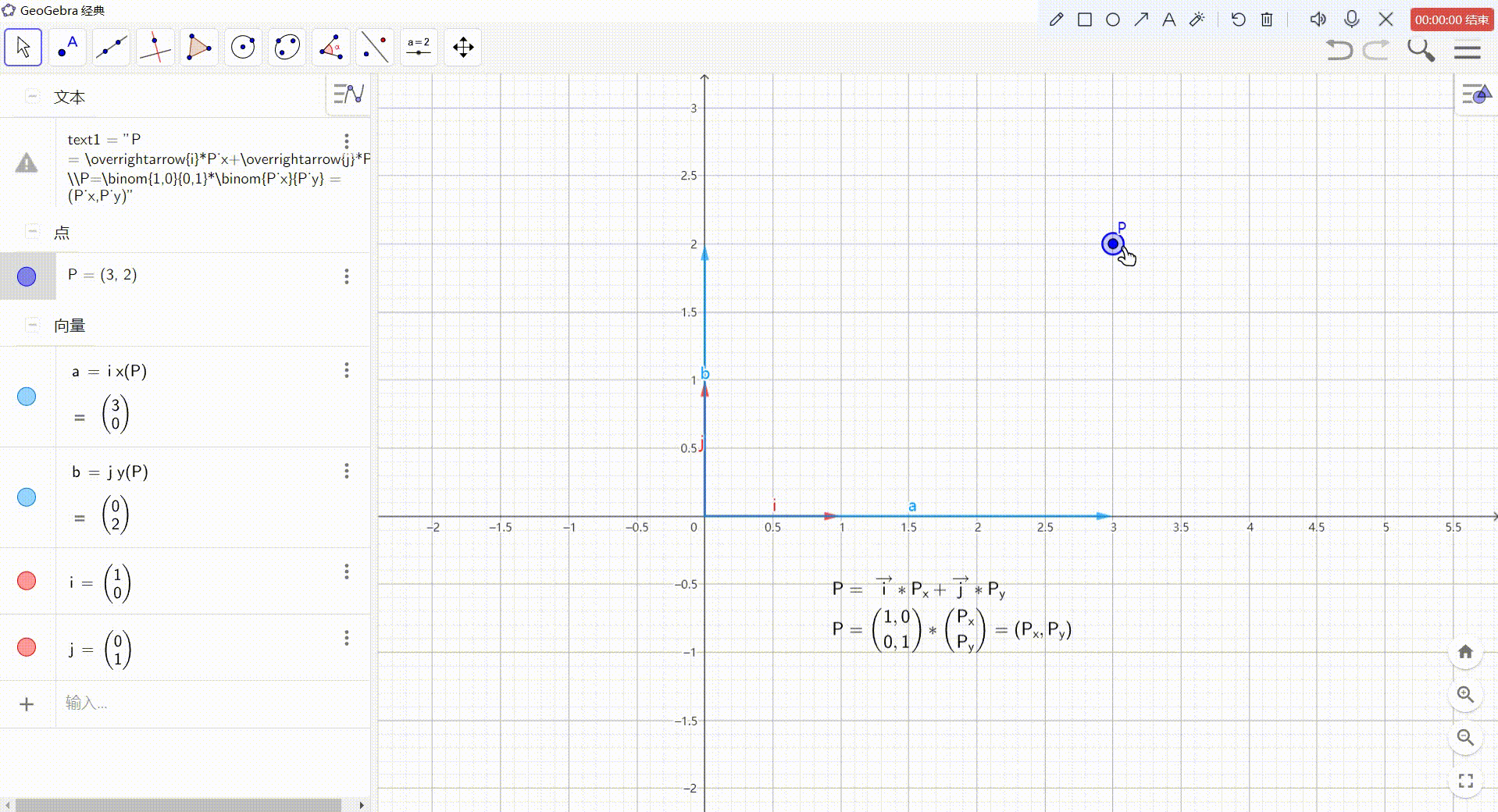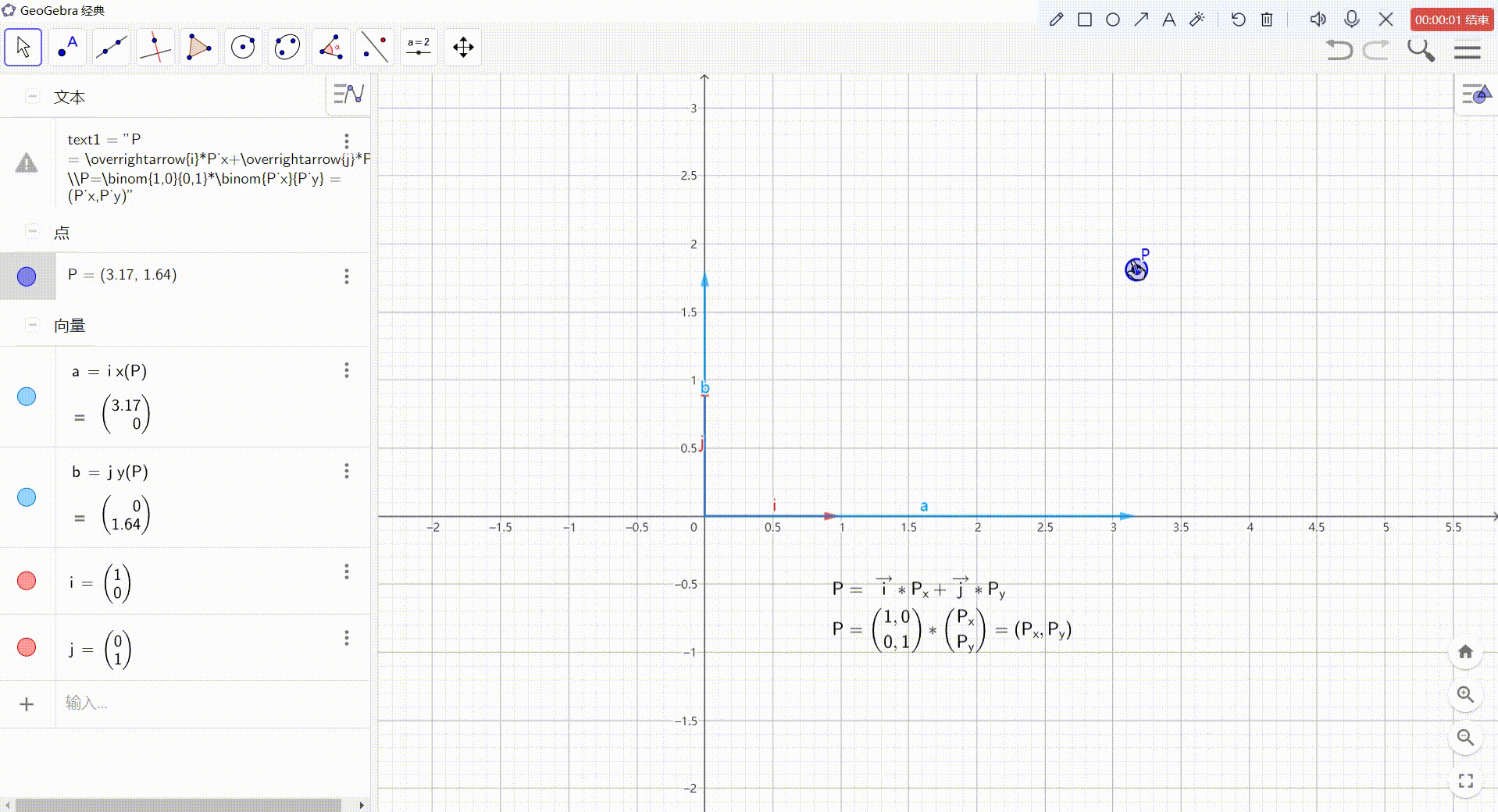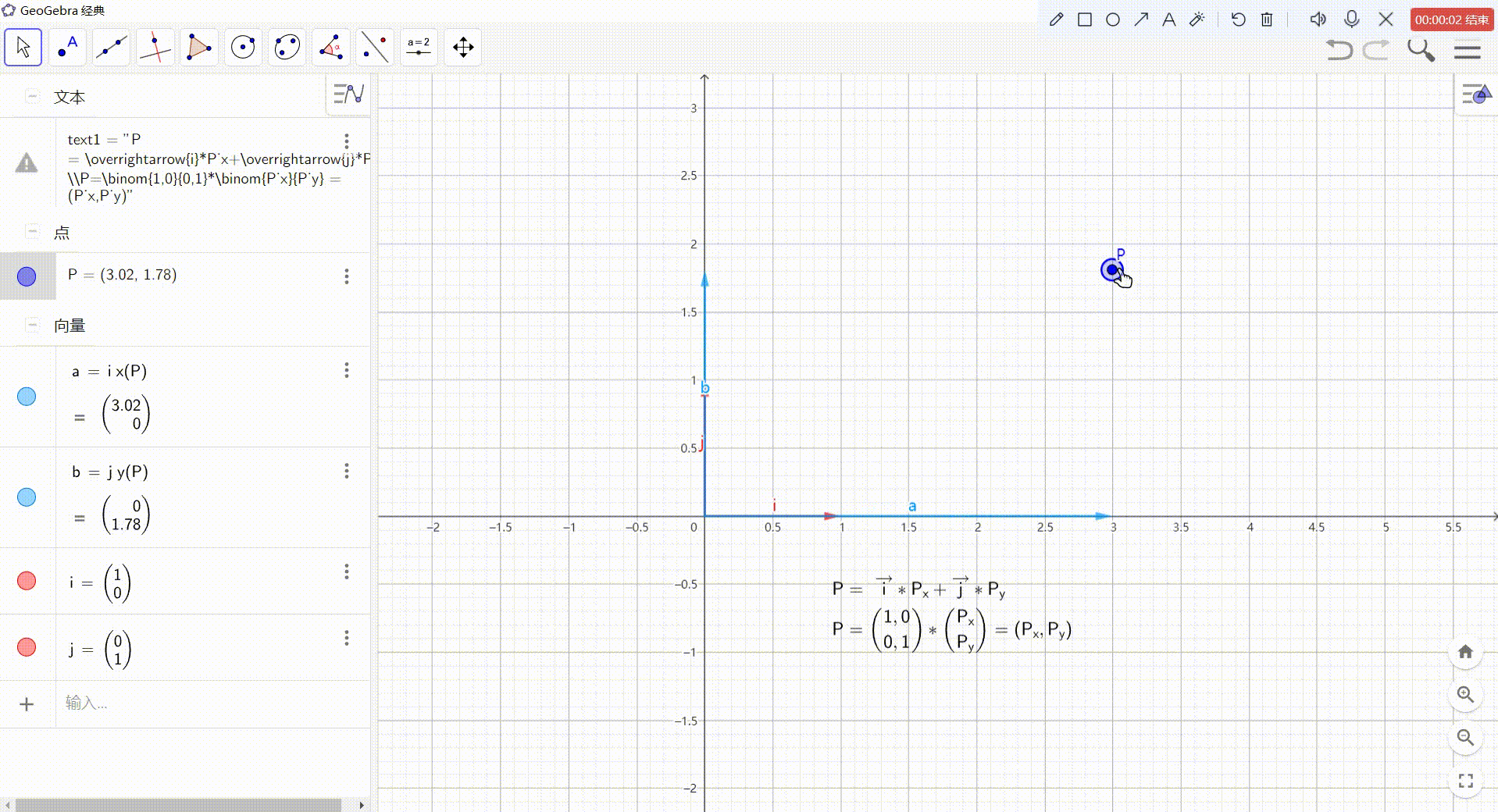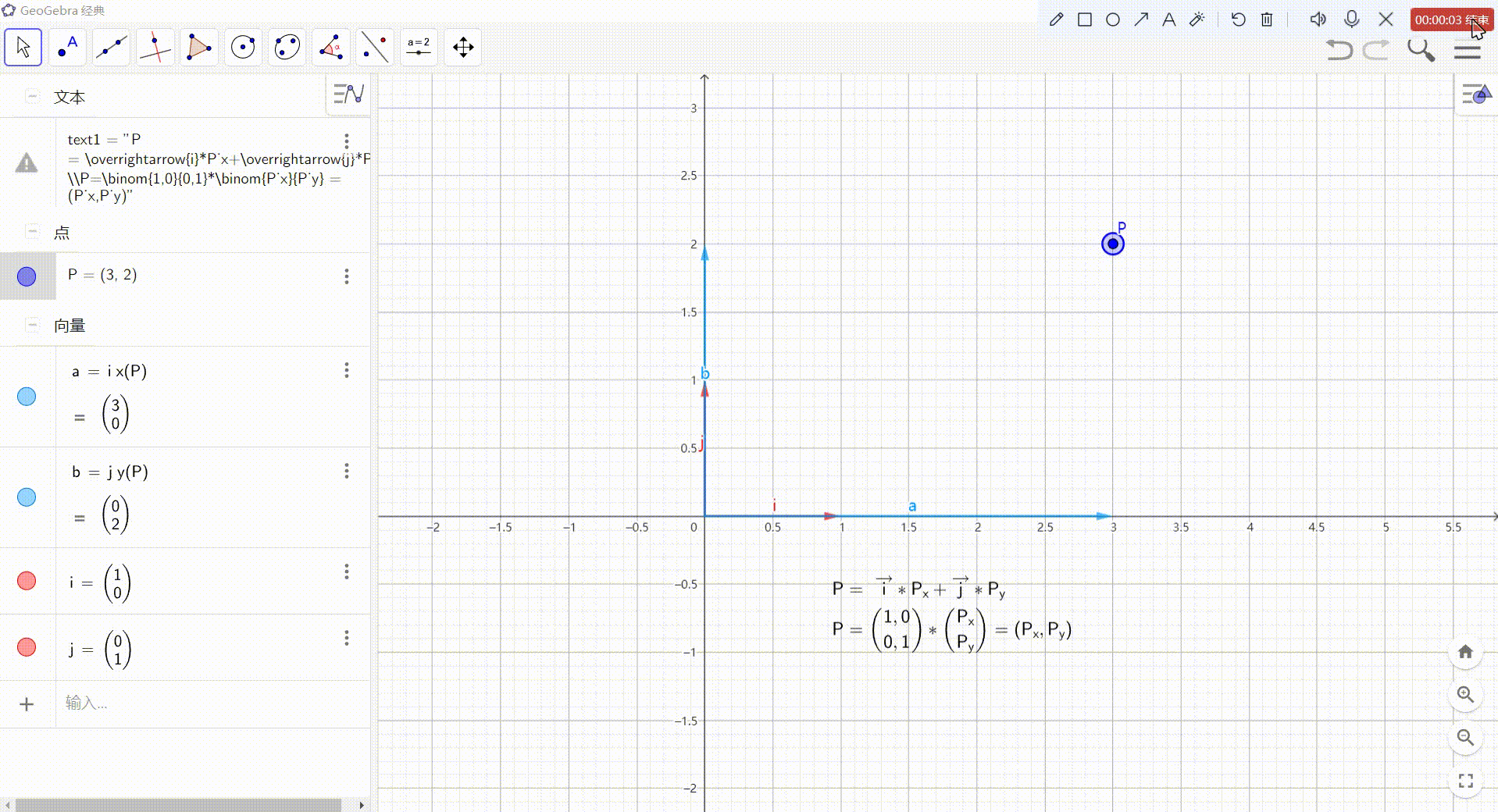
1、点 的 向量表达形式

• 点坐标 可以看作一个 从坐标原点 指向 点P的向量
• 可以把该向量分解为：两个坐标轴方向上的向量之和
• 坐标轴方向上的向量可以由：该坐标轴方向上的单位向量 乘以 P点对应的xy坐标值得到

这样就可以得到：P =$\vec{i}$ * P_x + $\vec{j}$ * P_y

2、点 的 矩阵表达形式

• P =$\vec{i}$ * P_x + $\vec{j}$ * P_y = (1,0) * P_x + (0,1) *P_y
  可以逆推理出：
• P =$\vec{i}$ * P_x + $\vec{j}$ * P_y = (1,0) * P_x + (0,1) *P_y

$$\begin{array}{cc}1& 0\\ 0& 1\end{array}$$
*
$$\begin{array}{c}Px\\ Py\end{array}$$

=
$$\begin{array}{c}PxPy\end{array}$$

= (P_x ,P_y)

---

二、使用二维旋转矩阵来旋转P点

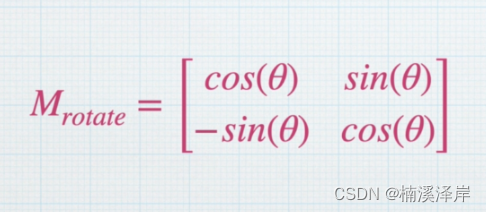
• P₃ = M_rotation * P₁
• P₄ = M_rotation * P₂
• c°是顺时针旋转的角度

---

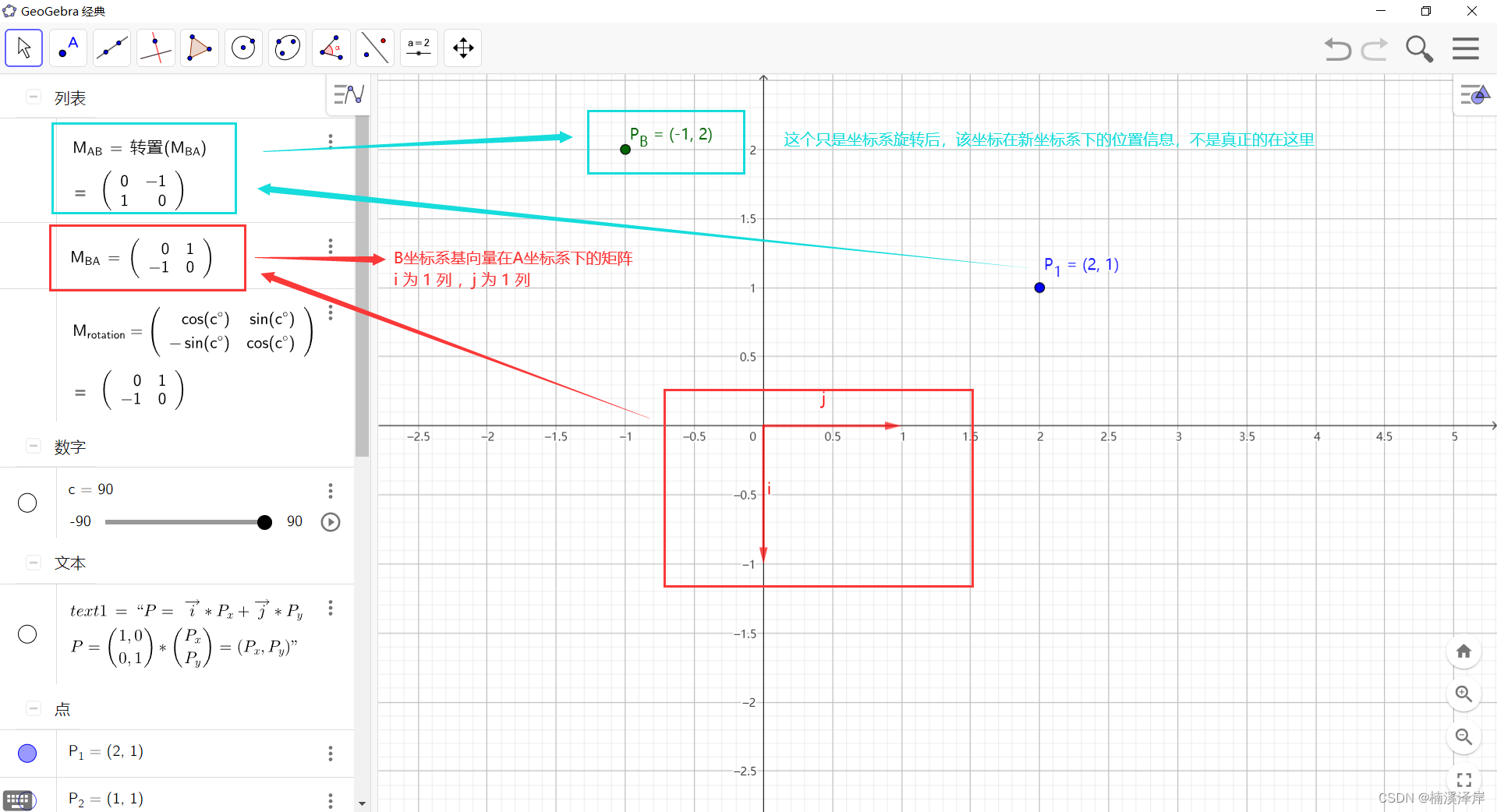
三、怎么求坐标系旋转后 P 点在新坐标系中的坐标

• [P_B] = [A_B] * [P_A]
  顶点P在B坐标系下的坐标 = A坐标系的基向量在B坐标系下的坐标所构成的矩阵 * 顶点P在A坐标系下的坐标
• [P_A] = [B_A] * [P_B]

顶点P在A坐标系下的坐标 = B坐标系的基向量在A坐标系下的坐标所构成的矩阵 * 顶点P在B坐标系下的坐标

• 因此，我们可以得出： A_B = B_A^-1

那么，我们要求 P 点在旋转后坐标系B下的坐标，可以这样求：

• 坐标系的基向量是互相垂直的单位向量，构成的矩阵刚好为正交矩阵
• 正交矩阵性质：逆矩阵 = 转置矩阵
• [P_B] = [B_A]^-1*[P_A]

1、我们求出 B 坐标系的基向量在 A 坐标系下的矩阵

B坐标系相对于A坐标系顺时针旋转了90°

• 基向量矩阵的构成方法：i 为一列，j为一列

2、求 B 坐标系的基向量在 A 坐标系下的矩阵的逆矩阵（转置矩阵）

3、[P_B] = [B_A]^-1*[P_A]

• P₁在B坐标系下看为（-1，2）
• P_B就是我们所求的结果