蓝桥杯--数的拆分
发布时间:2023年12月17日
蓝桥杯省赛 数的拆分,应该是一道数论的题目
连接:数的拆分

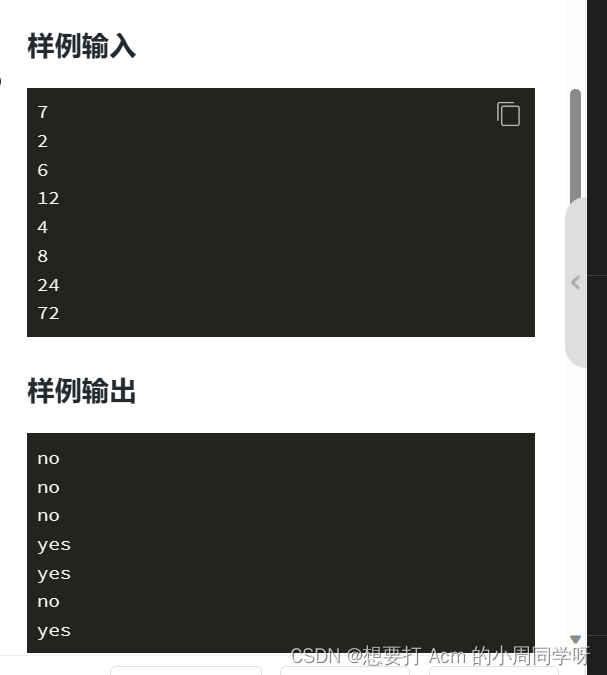

对有所有的样例,应该用long long 来表示。
n的范围是1e18次方,暴力绝对是行不通的,不能用暴力来解决。
这是一道数学的题目,需要对题目进行分析。因为要求y1 y2大于2。
关键点看出来 y1=2和y2等于3这种情况是一定符合的,所以我们对n进行质因数分解。
只要求出1e18开五次根号下面的是所有素数即可,大概400多,如果一个数字分解质因数,只出现了一次,输出no,因为此时不符合y2和y1都大于等于2的条件。当质因数分解完之后,需要判断n是否为平方数或者立方数即可,因为前面的质因数分解都是符合条件的,当一共数在n出现x次,那么肯定能拆分为2a+3b的形式,所以不管前面有多少组质因数,只要是符合条件的最后指数一定会是y1=2,y2=3的形式。
欧拉筛求质数,时间复杂度是on,速度快
void getprime()
{
int i, j;
for (i = 2; i <= 4500; i++)
{
if (!st[i])
{
prime.push_back(i);
}
for (j = 0; i * prime[j] <= 4500; j++)
{
st[i * prime[j]] = 1;
if (i % prime[j] == 0)
{
break;
}
}
}
}
求三次方的
int cbr(int x)
{
return x * x * x;
}
校验是否为一个数字的三次方或者平方
bool check(int x)
{
int a = (int)sqrt(x);
if (a * a == x) // 说明是一个数字的平方
{
return 1; // 是整数
}
int y = (int)cbrt(x); // 立法跟
if (cbr(y) == x || cbr(y + 1) == x || cbr(y - 1) == x)
{ // 数字太大有误差
return 1;
}
return 0;
}
主要逻辑方法
void solve()
{
int n;
cin >> n;
for (int i = 0; i < prime.size(); i++)
{
int x = prime[i]; // 得到对应的质数
int cur = 0;
if (n % x == 0)
{
while (n % x == 0)
{
n /= x;
cur++;
}
}
if (cur == 1)
{
cout << "no" << endl;
return;
}
}
// n已经变小了
if (check(n))
{
cout << "yes" << endl;
}
else
{
cout << "no" << endl;
}
}
main方法
signed main()
{
// 模板而已
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t = 1;
cin >> t;
getprime();
while (t--)
{
solve();
}
return 0;
}
全代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
vector<int> prime;
int st[5000];
// 线性筛保证时间是ON
void getprime()
{
int i, j;
for (i = 2; i <= 4500; i++)
{
if (!st[i])
{
prime.push_back(i);
}
for (j = 0; i * prime[j] <= 4500; j++)
{
st[i * prime[j]] = 1;
if (i % prime[j] == 0)
{
break;
}
}
}
}
int cbr(int x)
{
return x * x * x;
}
// 检验上是否为某个数字的立方根 平方跟或者其他的
bool check(int x)
{
int a = (int)sqrt(x);
if (a * a == x) // 说明是一个数字的平方
{
return 1; // 是整数
}
int y = (int)cbrt(x); // 立法跟
if (cbr(y) == x || cbr(y + 1) == x || cbr(y - 1) == x)
{ // 数字太大有误差
return 1;
}
return 0;
}
void solve()
{
int n;
cin >> n;
for (int i = 0; i < prime.size(); i++)
{
int x = prime[i]; // 得到对应的质数
int cur = 0;
if (n % x == 0)
{
while (n % x == 0)
{
n /= x;
cur++;
}
}
if (cur == 1)
{
cout << "no" << endl;
return;
}
}
// n已经变小了
if (check(n))
{
cout << "yes" << endl;
}
else
{
cout << "no" << endl;
}
}
signed main()
{
// 模板而已
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t = 1;
cin >> t;
getprime();
while (t--)
{
solve();
}
return 0;
}
文章来源:https://blog.csdn.net/ngczx/article/details/134954032
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【JavaEE进阶】 SpringBoot配置?件
- 助力城市部件[标石/电杆/光交箱/人井]精细化管理,基于YOLOv8全系列模型【n/s/m/l/x】开发构建生活场景下城市部件检测识别系统
- vue3-模版引用ref
- 更新钉钉文档封装好的代码
- 起点:如何成为一名黑客?
- 深入浅出AI落地应用分析:国内Top10应用
- leetcode | go | 第600题 | 不含连续1的非负整数
- 在香橙派5 Plus上搭建Gitlab
- MyBatis见解4
- 学习调整echarts中toolbox位置toolBox工具栏属性