175. 电路维修(BFS,双端队列)
发布时间:2023年12月18日
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。
翰翰的家里有一辆飞行车。
有一天飞行车的电路板突然出现了故障,导致无法启动。
电路板的整体结构是一个?R?行?C?列的网格(R,C≤500),如下图所示。
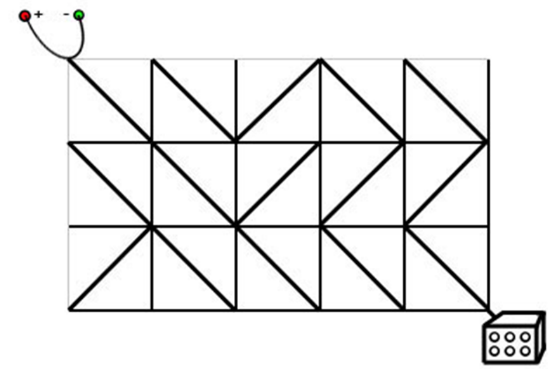
每个格点都是电线的接点,每个格子都包含一个电子元件。
电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。
在旋转之后,它就可以连接另一条对角线的两个接点。
电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。
达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。
她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。
不过,电路的规模实在是太大了,达达并不擅长编程,希望你能够帮她解决这个问题。
注意:只能走斜向的线段,水平和竖直线段不能走。
输入格式
输入文件包含多组测试数据。
第一行包含一个整数?T,表示测试数据的数目。
对于每组测试数据,第一行包含正整数?R?和?C,表示电路板的行数和列数。
之后?R?行,每行?C?个字符,字符是"/"和"\"中的一个,表示标准件的方向。
输出格式
对于每组测试数据,在单独的一行输出一个正整数,表示所需的最小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出?NO SOLUTION。
数据范围
1≤R,C≤500
1≤T≤5
输入样例:
1
3 5
\\/\\
\\///
/\\\\
输出样例:
1
样例解释
样例的输入对应于题目描述中的情况。
只需要按照下面的方式旋转标准件,就可以使得电源和发动机之间连通。
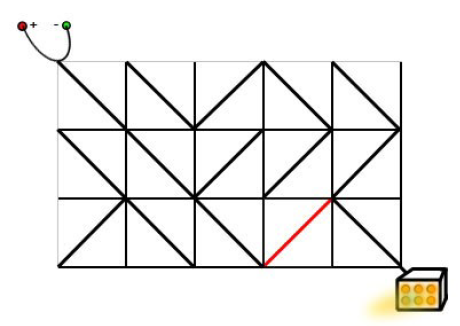
解析 :
性质:坐标和位偶数的点能走到,为奇数的点无法走到?
可以使用双端队列和bfs进行遍历,和迪杰斯特拉算法类似
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
using namespace std;
typedef long long LL;
const int N = 5e2 + 3;
typedef pair<int, int> PII;
int n, m;
char g[N][N];
int d[N][N];
int vis[N][N];
int bfs() {
memset(d, 0x3f, sizeof d);
memset(vis, 0, sizeof vis);
deque<PII>q;
char cs[5] = "\\/\\/";
int dx[] = { -1,-1,1,1 }, dy[] = { -1,1,1,-1 };
int ix[] = { -1,-1,0,0 }, iy[] = { -1,0,0,-1 };
d[0][0] = 0;
q.push_back({ 0,0 });
while (q.size()) {
int x = q.front().first;
int y = q.front().second;
q.pop_front();
if (x == n && y == m)return d[x][y];
if (vis[x][y])continue;
vis[x][y] = 1;
for (int i = 0,w; i < 4; i++) {
int a = x + dx[i], b = y + dy[i];
if (a<0 || a>n || b<0 || b>m)continue;
int ga = x + ix[i], gb = y + iy[i];
if (g[ga][gb] != cs[i])w = 1;
else w = 0;
if (d[x][y] + w <= d[a][b]) {
d[a][b] = d[x][y] + w;
if (!w)q.push_front({ a, b });
else q.push_back({ a,b });
}
}
}
return -1;
}
int main() {
int T;
cin >> T;
while (T--) {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
scanf("%s", g[i]);
}
if ((n + m) % 2 != 0) {
printf("NO SOLUTION\n");
}
else {
printf("%d\n", bfs());
}
}
return 0;
}?
文章来源:https://blog.csdn.net/Landing_on_Mars/article/details/135072503
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【笔试强训】Day1选择题
- 03_Web开发基础之综合应用
- ssh免密登录 ssh公钥分发 ssh密钥生成
- 基于LLaMA Factory,单卡3小时训练专属大模型 Agent
- 2024.1.14~1.20 周内刷题总结
- 仿真机器人-深度学习CV和激光雷达感知(项目2)day01
- 苏州和数荣获苏州市软件行业协会“杰出贡献理事单位”
- Python搭建代理IP池实现存储IP的方法
- Spring MVC 参数接收
- Python进阶-Anaconda使用总结