Codeforces Round 890 (Div. 2) supported by Constructor Institute补题

Tales of a Sort（Problem - A - Codeforces）

题目大意：给定一个n长数组a[],我们可以进行若干次操作，每次操作可以将数组中所有的a[i]执行操作：a[i]=max(a[i]-1,0);最后要得到一个n非递减数组，问最少需要操作多少次。

思路：显然数组中所有的数是同步变化的，所以相对大小不变，除非到0，那么不再变化。所以我们就得到第一条规律：如果数组中的数满足题目要求，那么就不用执行操作，如果一旦不满足条件，那么就要执行操作。然后就来考虑执行多少次呢？全变成0自然可以，但是有没有更少的次数呢，显然我们只要把不满足的位置处理成满足就可，不满足的位置就是前面比后面大，我们只要让前面变成0，那么后面一定也变成0了，那么满足条件了。所以我们只需要统计出所有不满足位置的最大值。

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		int mx=0;
		int flag=1,c;
		cin>>c;
		for(int i=1;i<n;i++)
		{
			int x;
			scanf("%d",&x);
			if(c>x) mx=max(mx,c),flag=0;
			c=x;
		}
		if(flag)printf("0\n");
		else printf("%d\n",mx);
	}
}

Good Arrays（Problem - B - Codeforces）

题目大意：现有一个正整数数组a[],我们要构造一个正整数数组b[],使得a[],b[]满足a[i]!=b[i],但sum(a[i])==sum(b[i]),问这样的b[]是否存在。

样例：

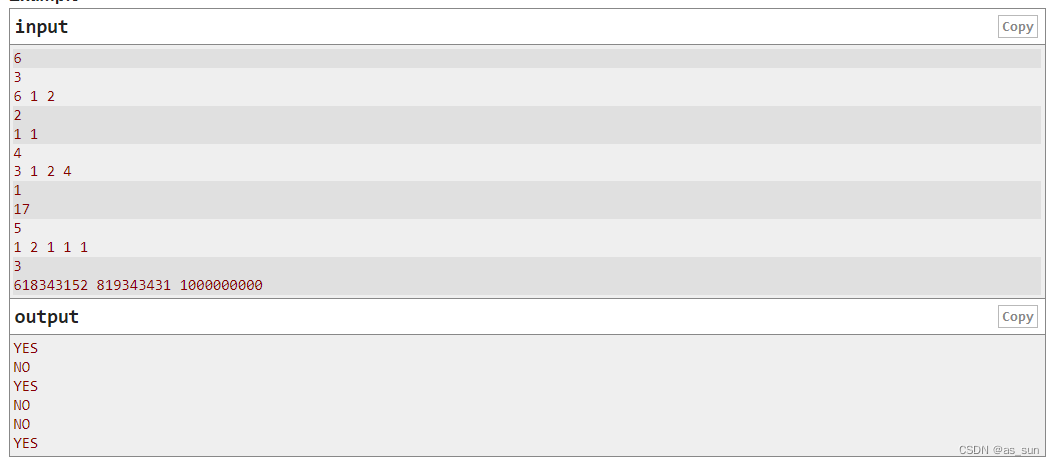
思路：我们根据样例来看，发现可以将所有非1的位置变成1，多余的数拿出来填给为1的位置，这样就可以实现，如果从非1的位置拿出来的数，不能保证每个1位置都补一个的话，那么一定不可以。

#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		int n;
		scanf("%lld",&n);
		int sum=0,x,c=0;
		for(int i=1;i<=n;i++) scanf("%lld",&x),sum += (x-1),c += x==1?1:0;
		if(n==1) printf("NO\n");
		else
		{
			if(sum>=c) printf("YES\n");
			else printf("NO\n");
		}
	}
}

To Become Max（Problem - C - Codeforces）

题目大意：现有一个数组a[]，我们最多可以执行k次以下操作：

1.选一个位置i且保证a[i]<=a[i+1]

2.a[i]+=1;

需要求出最后的max(a[i]).

思路：这道题我首先想用动态规划，从后往前，定义dp[i][j]表示已经访问i个了，用的操作数不超过j的情况下，得到的最大值。然后枚举每个位置的最大操作次数，来更新k，但很显然每个位置的操作与上个位置有关，我们dp[i][j]没办法得到当前位置更新成什么数了，所以没办法确定下个位置可以更新成什么数。后来又想着用dfs来写，虽然可以把情况考虑清楚，但是很明显超时了。所以也不行。

然后我去看了题解，题解的方法很妙，因为k的范围很大，进而可以进行的操作就很多，但实际上我们有一个最大上限，将k累加到原数组的最大值上，就能得到上限，为0的时候就是下限。那么显然这里可以直接二分来写，我们从这个范围内找一个数作为最大值tm，然后循环n位，判断这个最大值出现在第i位上时，需要进行的操作数，这里我们可以从i往后找，因为第i位的操作次数就是tm-a[i],下一位最大只用到tm-1即可，依次往后找，找到操作数超过或者找到当前的数大于等于目标数(大于等于目标数的话实际就不用变，后面的自然也不用更改了)停。判断操作次数是否符合要求，然后更改边界继续二分。另外数据范围可能会爆，要用longlong

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,k,a[4000];
int check(int u)
{
	for(int i=1;i<=n;i++)
	{
		int t=u,c=0;
		for(int j=i;j<=n;j++)
		{
			if(a[j]>=t) break;
			if(j==n) 
			{
				c=k+1;
				break;//第n位不能动，后面没有数了
			}
			c+=t-a[j];
			t=max(0ll,t-1);
		}
		if(c<=k) return 1;
	}
	return 0;
}
signed main()
{
	int t;
	scanf("%lld",&t);
	while(t--)
	{
		scanf("%lld%lld",&n,&k);
		int mx=0;
		for(int i=1;i<=n;i++) scanf("%lld",&a[i]),mx=max(mx,a[i]);
		int l=0,r=mx+k;
		while(l<r)
		{
			int mid=(l+r+1)/2;
			if(check(mid))l=mid;
			else r=mid-1;
		}
		cout<<l<<endl;
	}
}

?More Wrong（Problem - D - Codeforces）

题目大意：交互题，内置一个长为n的排列，我们每次可以询问[l,r]区间中逆序对的数量，要在5*n*n次询问内找出最大数的下标。

思路：很容易发现如果[l,r]中的逆序对数量和[l,r-1]中的逆序对数量相同，那么r处应该是[l,r]区间中的最大数，但它未必是整个排列的最大数，所以我最开始想的是先找[1,r-1]和[1,r]，再看r的后面，求[r,n]和[r+1,n]如果差值刚好是（n-r）的话，那么就说明r前面的数都比它小，后面的数都比它大，那么它就是最大数，但是如果从后往前遍历，在可能的位置访问一下后缀是会超时的。

所以这道题不能暴力，逆序对可以联想到归并排序，那么这题实际可以用分治的思路来写，不断分小。核心思想就是分治，找出每个区间内的最大的数，然后再找区间与区间之间的最大的数，难点在于区间与区间之间最大的数怎么找，我们只要让两个区间中的最大的数分别为头和尾进行区间查询，在这个区间中最大的数要么在开头，要么在结尾，那么只要判断结尾的数是不是，如果是，那么就是，否则就在开头。

a,b,c,d

首先进行a,b的比较判断出a更大（[a,b]>[a,a],[a,a]返回0）

然后c,d也会在同一层进行比较，([c,d]==[c,c],[c,c]同上)

回到上一层那么就是[a,d]与[a,d-1]比较

返回a或者d

#include<bits/stdc++.h>
using namespace std;
int query(int a,int b)
{
	if(a==b) return 0;//这里一定要记得处理，相同的是无法进行询问的
	printf("? %d %d\n",a,b);
	fflush(stdout);
	int c;
	scanf("%d",&c);
	return c;
}
int fz(int a,int b)//分治函数，将区间拆开
{
	if(a==b) return a;
	int mid=(a+b)/2;
	int l=fz(a,mid),r=fz(mid+1,b);
	int x=query(l,r);
	int y=query(l,r-1);
	//根据查询值判断当前区间的返回值
	if(x==y) return r; 
	else return l;
}
int main()
{
	int t;
	scanf("%d",&t);
	while(t--)
	{
		int n;
		scanf("%d",&n);
		int ans=fz(1,n);
		printf("! %d\n",ans);
		fflush(stdout);
	}
}

PermuTree (easy version)（Problem - E1 - Codeforces）

题目大意：现有一个n长排列，同时是一棵以1为根节点的树，我们同时知道每个点的父节点，要求给出排列的顺序，求满足a[l]<a[lca(l,r)]<ar的(l,r)对数的和的最大值。

思路：

我们先来看第一个样例，据此理解下题意：

我们以这个图为例，显然就是让根节点在中间，然后左边子树的节点个数*右边子树的节点个数就是我们要求的点对数。?那么我们只用dfs求出子树中点的个数，然后再直接相乘？当然不是，这只是个特例，因为在这个例子中构成的是一棵二叉树，

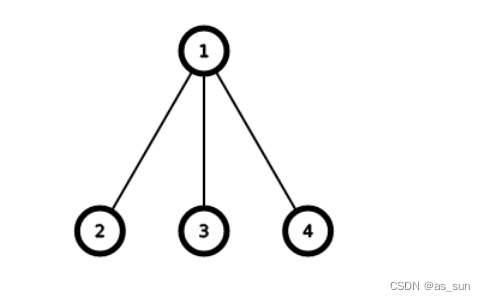
这个例子中就只有两对，因为在排列中1只能在2,3或者3,4之间，那么问题就转换成了如果分配使得左边所有子树的节点和*右边所有子树的节点和的值最大，显然两边总的节点数一定为all,那么假设左边是l,右边就是all-l,乘积最大的话l*(all-l)最大，那么l应该尽量离all/2更近。我本来就是用这个思路贪心来写，也就是排序，然后累加，在all/2左右计算一下结果，但是不太凑巧，第七个样例过不了。然后看了题解发现，这里是将问题转化成01背包问题，就是求总个数一定的情况下，将每棵子树视为一个物品，求这些物品能凑出的节点和，实际就是求若干个数能凑出哪些数，通过凑出的这些数来求能得到的最大值，把它加进结果中去。

#include<bits/stdc++.h>
using namespace std;
int h[1000010],e[1000010],ne[1000010],dp[1000010],idx;
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int ans,n;
int dfs(int u)
{
	int c=1;
	vector<int>p;
	p.push_back(0);
	for(int i=h[u];i!=-1;i=ne[i])
	{
		int j=e[i];
		int t=dfs(j);
		p.push_back(t);
		c += t;
	}
	if(c==1) return 1;
	sort(p.begin(),p.end());
	int mx=0,all=c-1;
	memset(dp,0,sizeof dp);
	dp[0]=1;
	for(int i=1;i<p.size();i++)//枚举物品
	{
		for(int j=all;j>=p[i];j--)
		{
			dp[j]+=dp[j-p[i]];
			if(dp[j]) mx=max(j*(all-j),mx);
		}
	}
	/*int all=c-1;
	int s=0;
	int mx=0;
	for(int i=0;i<p.size();i++)
	{
		s+=p[i];
		mx=max(mx,(all-s)*s);
	}*/
	ans += mx;
	return c;
}
int main()
{
	memset(h,-1,sizeof h);
	scanf("%d",&n);
	for(int i=2;i<=n;i++)
	{
		int x;
		scanf("%d",&x);
		add(x,i);
	}
	ans=0;
	dfs(1);
	cout<<ans<<endl;
}

?PermuTree (hard version)（Problem - E2 - Codeforces）

等我dp全部学完再来填这个坑，这里和上题的主要思路大差不差，主要是用到二进制优化。