【学习总结】地面路谱分析

本文仅用于记录自己的学习总结，包括个人理解。不保证内容严格正确。

0. 参考资料

• [1] 国标GB/T 703-2005/ISO 8608:1995。
• [2] Bilibili 路面不平度统计特性
• [3] 网络参考文档.

网盘：https://pan.baidu.com/s/1ameuQwdOquCrk2V1PIS-Xw?pwd=ut9m

1. 路面空间功率谱密度 $G_q(n)$

$G_q(n)=G_q(n_0)(\frac{n}{n_0}{)}^{?w}$
n：空间频率，单位 $m^{?1}$，表示“每米长度有几个波长”，对应常说的“时间频率”，及 $1/s,Hz$
n0：参考空间频率，为固定值，$n_0=0.1m^{?1}$
$G_q(n_0)$：参考空间频率下的路面功率谱密度，即“路面不平度系数”
W：频率指数，一般取 2。没什么原因，就是一般取2。

关于式子的理解：
当我们知道路面的不平度系数 $G_q(n_0)$ 后，可以计算出功率密度谱。

$G_q(n_0)$的取值？
根据路面分级，有几何平均值。

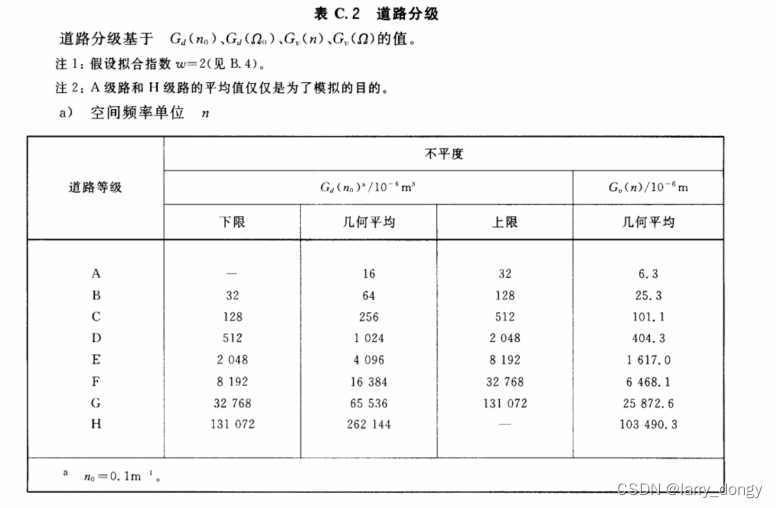
2. 速度/加速度功率谱密度

速度功率谱密度：$G_v(n)=(2\pi n{)}^2{G}_q(n)$
加速度功率谱密度：$G_a(n)=(2\pi n{)}^4{G}_q(n)$

当 $W=2$ 时，速度的表达式为：$G_v(n)=(2\pi n{)}^2{G}_q(n_0)$，此时与$n$无关了。很独特的情况。

3. 时间频率功率谱密度 $G_q(f)$

上述的谱密度是空间的，没有考虑车速。如果考虑到车速，应该有入如下表达式：
$f=vn$，即 “时间频率=车速*空间频率”，对应量纲 $Hz=m/s?m^{?1}$ 也是合理的。

此时，可以得到 位移/速度/加速度的时间频率功率谱密度分别为：
位移：$G_q(f)=\frac{1}{v}{G}_q(n_0)(\frac{n}{n_0}{)}^2=G_q(n_0)n_0^2\frac{v}{f^2}$
速度：$G_v(f)=4{\pi }^2{G}_q(n_0)n_0^{2}v$
加速度：$G_a(f)=16{\pi }^4{G}_q(n_0)n_0^{2}v{f}^2$
可以看出，速度的和$f$无关。

对功率谱密度，左右都取对数，可以得到一条直线；横轴是频率f，纵轴是$G_{q/v/a}(f)$，注意纵轴的单位也不一样。

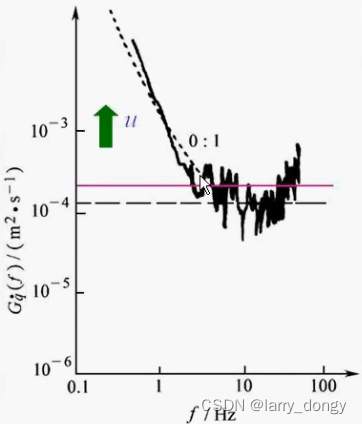
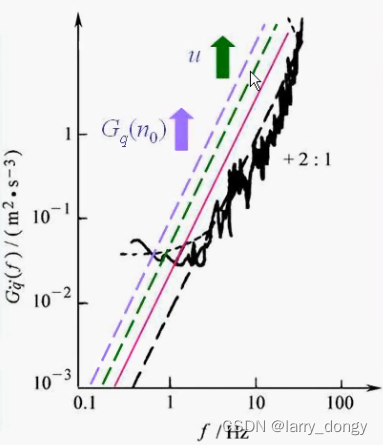
4. 关于拟合

国际/国标中，考虑的是空间频率 $n=0.0112.83$ 之间的曲线，这个数值应该是经验值。

一些论文中，可能有分段拟合，对测得的 $G_p(n)$ 进行拟合，可以得到$W$和$G_d(n_0)$，后者可以结合上面的表格，判断所属的地面等级。或者画出曲线，和 A~H 这几个国家规定的等级对应的曲线进行比较，可以得出路面的等级。

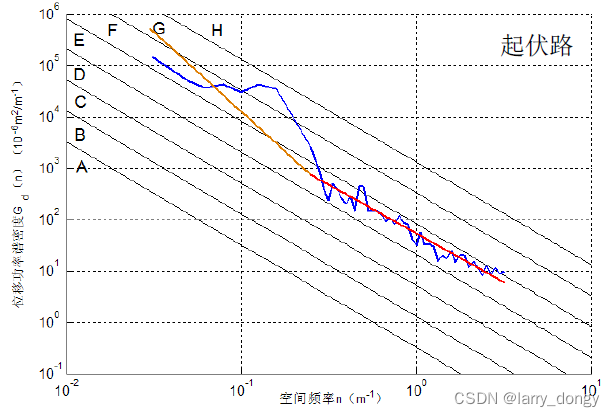
5. 一些其它操作

关于国标文件中一些计算/说明的理解：

倍频程带宽：
由于在计算功率密度时，需要选择一定的带宽，计算“落入”这个区间的功率，带宽的选择比较重要。国标给出了：倍频程带宽、1/3倍频程、和1/12倍频程，表示不断的精细，下面这个表就是不同选择下每个“中心频率”和左右两端频率的取值。