【算法与数据结构】474、LeetCode一和零

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

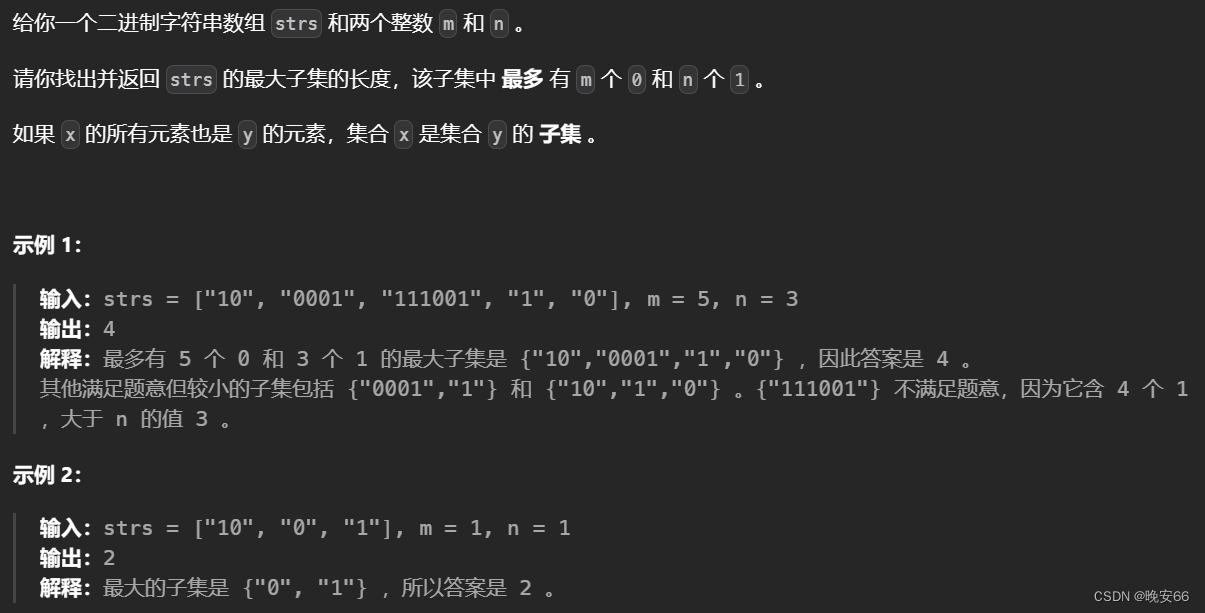
二、解法

??思路分析：本题要找strs数组的最大子集，这个子集最多含有$m$个0和$n$个1。本题也可以抽象成一个01背包的问题。其中，strs内的元素就是物品，而$m$和$n$就是背包的维度。$dp[i][j]$代表最多有i个0和j个1的strs的最大子集的大小。递归数组可以由$dp[i][j]=max(dp[i][j],dp[i?zeroNum][j?oneNum]+1)$得出。和文章【算法与数据结构】算法与数据结构知识点中的01背包滚动数组一样，循环需要从后往前进行，否则会将strs重复计算。
??程序如下：

class Solution {
public:
	int findMaxForm(vector<string>& strs, int m, int n) {
		vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));	// 默认初始化为0
		for (string str : strs) {	// 遍历物品
			int oneNum = 0, zeroNum = 0;
			for (char c : str) {
				if (c == '0') zeroNum++;
				else oneNum++;
			}
			for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
				for (int j = n; j >= oneNum; j--) {
					dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
				}
			}
		}
		return dp[m][n];
	}
};

复杂度分析：

• 时间复杂度： $O(K?m?n)$，K为strs的长度。
• 空间复杂度：$O(m?n)$。

三、完整代码

# include <iostream>
# include <vector>
# include <string>
using namespace std;

class Solution {
public:
	int findMaxForm(vector<string>& strs, int m, int n) {
		vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));	// 默认初始化为0
		for (string str : strs) {	// 遍历物品
			int oneNum = 0, zeroNum = 0;
			for (char c : str) {
				if (c == '0') zeroNum++;
				else oneNum++;
			}
			for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历！
				for (int j = n; j >= oneNum; j--) {
					dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
				}
			}
		}
		return dp[m][n];
	}
};

int main() {
	Solution s1;
	vector<string> strs = { "10", "0001", "111001", "1", "0" };
	int m = 5;
	int n = 3;
	int result = s1.findMaxForm(strs, m, n);
	cout << result << endl;
	system("pause");
	return 0;
}

end