算法中的最优化方法课程复习
算法中的最优化方法课程复习
单模函数、拟凸函数、凸函数
单模函数
注意符号是小于等于，可以取等于号。
拟凸函数
凸函数
例子1
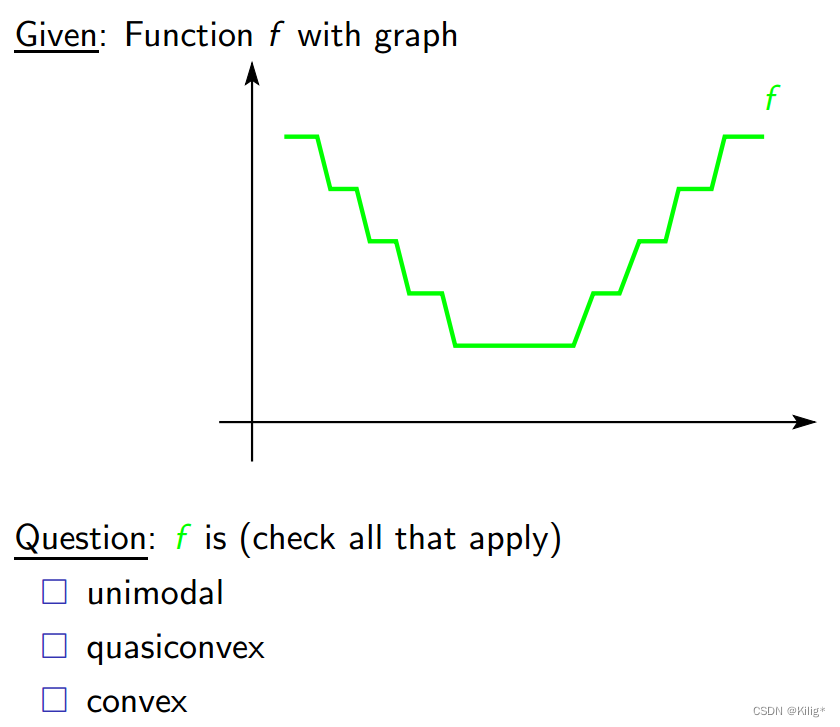
根据上面的性质判断，这个函数同时是拟凸函数、单模函数，但不是凸函数。
例子2
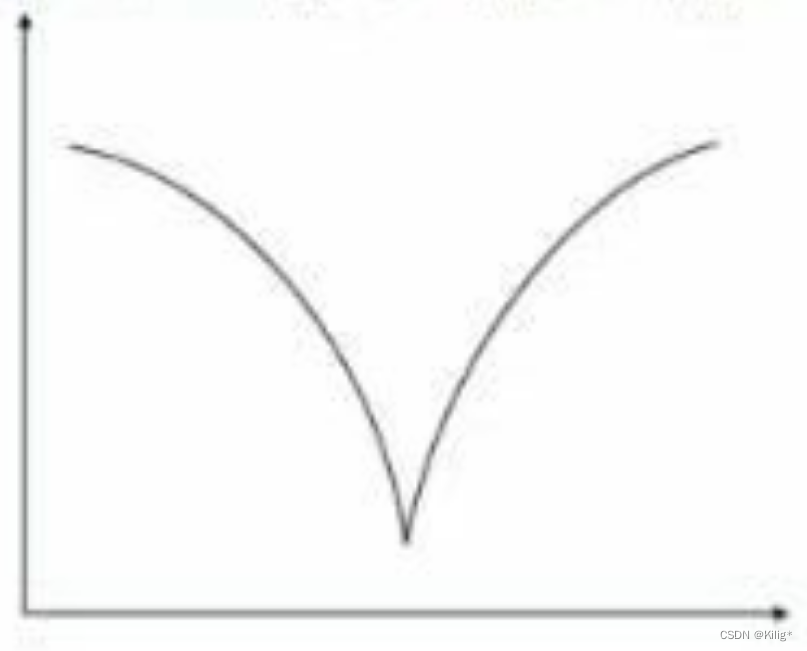
根据上面的性质判断，函数是单模函数、拟凸函数，但并不是凸函数。
证明
证明一个线性函数与一个凸函数的和也是凸的
设
f
(
x
)
=
g
(
x
)
+
h
(
x
)
f(x) = g(x) + h(x)
f(x)=g(x)+h(x)其中
g
(
x
)
g(x)
g(x)是一个凸函数
h
(
x
)
h(x)
h(x)是一个线性函数(下面我们可以看出，线性函数也是凸函数)。
因此有以下性质
g
(
λ
x
+
(
1
?
λ
)
y
)
<
=
λ
g
(
x
)
+
(
1
?
λ
)
g
(
y
)
g(\lambda x+(1-\lambda )y) <=\lambda g(x) + (1-\lambda)g(y)
g(λx+(1?λ)y)<=λg(x)+(1?λ)g(y)以及
h
(
λ
x
+
(
1
?
λ
)
y
)
<
=
λ
h
(
x
)
+
(
1
?
λ
)
h
(
y
)
h(\lambda x+(1-\lambda )y) <= \lambda h(x) + (1-\lambda)h(y)
h(λx+(1?λ)y)<=λh(x)+(1?λ)h(y)
开始证明:
f
(
λ
x
+
(
1
?
λ
)
y
)
=
g
(
λ
x
+
(
1
?
λ
)
y
)
+
h
(
λ
x
+
(
1
?
λ
)
y
)
<
=
λ
g
(
x
)
+
(
1
?
λ
)
g
(
y
)
+
λ
h
(
x
)
+
(
1
?
λ
)
h
(
y
)
=
λ
(
g
(
x
)
+
h
(
x
)
)
+
(
1
?
λ
)
(
g
(
y
)
+
h
(
y
)
)
=
λ
(
f
(
x
)
)
+
(
1
?
λ
)
(
f
(
y
)
)
f(\lambda x+(1-\lambda )y) \\ \qquad \qquad \qquad = g(\lambda x+(1-\lambda )y) + h(\lambda x+(1-\lambda )y) \\ \qquad \qquad \qquad \qquad \quad <=\lambda g(x) + (1-\lambda)g(y) +\lambda h(x) + (1-\lambda)h(y) \\ \qquad \qquad \qquad = \lambda (g(x)+h(x)) + (1-\lambda)(g(y)+h(y)) \\ = \lambda (f(x)) + (1-\lambda)(f(y))
f(λx+(1?λ)y)=g(λx+(1?λ)y)+h(λx+(1?λ)y)<=λg(x)+(1?λ)g(y)+λh(x)+(1?λ)h(y)=λ(g(x)+h(x))+(1?λ)(g(y)+h(y))=λ(f(x))+(1?λ)(f(y))得证
其他如凸函数于凸函数的和仍为凸函数，也是如此证明。
梯度
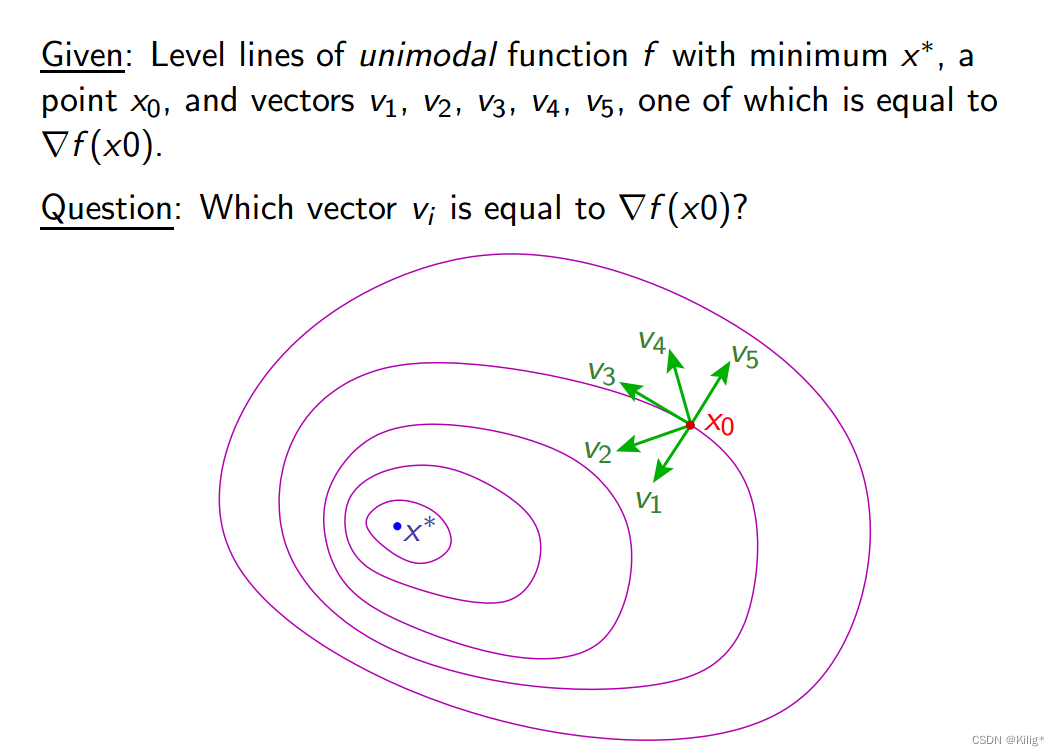
负梯度方向是从当前来看函数值下降最快的方向，所以V1是负梯度方向，而梯度方向与负梯度方向相反。所以V5是梯度方向。（梯度方向与负梯度方向垂直于等值线的切线）
线性规划标准形式以及如何标准化
标准形式
目标函数：最小化
Minimize
c
?
x
\text{Minimize} \quad \mathbf{c}^\top \mathbf{x}
Minimizec?x
约束条件：
Subject?to
A
x
=
b
x
≥
0
\begin{align*} \text{Subject to} \quad & \mathbf{Ax} = \mathbf{b} \\ & \mathbf{x} \geq \mathbf{0} \end{align*}
Subject?to?Ax=bx≥0?
其中，
- c \mathbf{c} c 是目标函数的系数向量；
- x \mathbf{x} x 是决策变量向量；
- A \mathbf{A} A 是约束系数矩阵；
- b \mathbf{b} b 是约束右端项向量。
常见标准化方法
接下来以几个例子说明常见的标准化方法
m
a
x
7
x
1
+
2
x
2
?
2
x
3
+
8
s
.
t
.
x
1
?
2
x
2
+
3
x
3
?
8
x
4
<
=
6
x
1
?
x
3
<
=
5
0
<
=
x
1
<
=
9
x
2
<
=
1
max \qquad 7x_1 + 2x_2 - 2x_3 + 8 \\s.t. \qquad x_1-2x_2+3x_3-8x_4<=6 \\ \qquad x_1 - x_3<=5 \\ \qquad 0<=x_1<=9 \\ \qquad x_2<=1
max7x1?+2x2??2x3?+8s.t.x1??2x2?+3x3??8x4?<=6x1??x3?<=50<=x1?<=9x2?<=1
- 通过目标函数统一乘以-1将max优化问题转为min优化问题
- 对于<=的不等式约束，加上一个非负的变量使其变为等式约束
- 对于>=的不等式约束，减去一个非负的变量使其变为等式约束
- 对于x<=0之类的约束，变为 -x>=0
- 对于x正负无限制的变量，利用两个非负变量令
x
=
x
1
?
x
2
,
x
1
>
=
0
,
x
2
>
=
0
x = x_1-x_2 ,x_1>=0,x_2>=0
x=x1??x2?,x1?>=0,x2?>=0化为非负变量
因此上面的线性规划问题可以标准化如下
m a x 7 x 1 + 2 x 2 ? 2 x 3 + 8 s . t . x 1 ? 2 x 2 + 3 x 3 ? 8 x 4 + x 5 = 6 x 1 ? x 3 + x 6 = 5 x 1 + x 7 = 9 x 2 + x 8 = 1 x 1 , x 5 , x 6 , x 7 , x 8 > = 0 max \qquad 7x_1 + 2x_2 - 2x_3 + 8 \\s.t. \qquad x_1-2x_2+3x_3-8x_4+x_5=6 \\ \qquad x_1 - x_3 + x_6=5 \\ \qquad x_1 + x_7=9 \\ \qquad x_2 + x_8=1 \\ \qquad x_1,x_5,x_6,x_7,x_8>=0 max7x1?+2x2??2x3?+8s.t.x1??2x2?+3x3??8x4?+x5?=6x1??x3?+x6?=5x1?+x7?=9x2?+x8?=1x1?,x5?,x6?,x7?,x8?>=0
由于 x 2 , x 3 , x 4 x_2,x_3,x_4 x2?,x3?,x4?并没有非负性的限制，因此需要把这些变量也做一定的变换。
令 x 2 = x 9 ? x 10 , x 3 = x 11 ? x 12 , x 4 = x 13 ? x 14 x_2 = x_9 - x_{10},x_3 = x_{11}-x_{12},x_4 = x_{13}-x_{14} x2?=x9??x10?,x3?=x11??x12?,x4?=x13??x14?且有 x 9 . . . x 14 > = 0 x_9...x_{14}>=0 x9?...x14?>=0
原线性规划问题可以变为
m a x 7 x 1 + 2 ( x 9 ? x 10 ) ? 2 ( x 11 ? x 12 ) + 8 s . t . x 1 ? 2 ( x 9 ? x 10 ) + 3 ( x 11 ? x 12 ) ? 8 ( x 13 ? x 14 ) + x 5 = 6 x 1 ? ( x 11 ? x 12 ) + x 6 = 5 x 1 + x 7 = 9 ( x 9 ? x 10 ) + x 8 = 1 x 1 , x 5 , x 6 , x 7 , x 8 , x 9 . . . x 14 > = 0 max \qquad 7x_1 + 2(x_9 - x_{10}) - 2(x_{11}-x_{12}) + 8 \\s.t. \qquad x_1-2(x_9 - x_{10})+3(x_{11}-x_{12})-8(x_{13}-x_{14})+x_5=6 \\ \qquad x_1 - (x_{11}-x_{12})+ x_6=5 \\ \qquad x_1 + x_7=9 \\ \qquad (x_9 - x_{10}) + x_8=1 \\ \qquad x_1,x_5,x_6,x_7,x_8,x_9...x_{14}>=0 max7x1?+2(x9??x10?)?2(x11??x12?)+8s.t.x1??2(x9??x10?)+3(x11??x12?)?8(x13??x14?)+x5?=6x1??(x11??x12?)+x6?=5x1?+x7?=9(x9??x10?)+x8?=1x1?,x5?,x6?,x7?,x8?,x9?...x14?>=0
线性化技巧
有待更新
单纯形法
二次规划
有待更新
无约束优化
多维无约束优化（牛顿法、BFGS、DFP、Levenberg-Marquardt）
Nelder-Mead
Nelder-Mead方法在优化过程中不需要用到导数，但是在优化变量个数较多时相对没那么高效。
线搜索
FR共轭梯度法
例题
什么是最速下降法?最速下降法的步聚是什么?最速下降法是不是一定能够最快搜索到最优解?如果是请阐述原因，如果不是，请说明什么情况下不能，可以采用什么方法更高效，为什么?
最速下降法用于寻找多元函数的局部最小值。它的核心思想是沿着目标函数的梯度方向迭代地调整参数值，以达到逐渐接近最优解的目的。
步骤：
- 初始值设置： 选择初始点 x 0 \mathbf{x}_0 x0?。
- 计算梯度： 在当前点计算目标函数的梯度 ? f ( x ) \nabla f(\mathbf{x}) ?f(x)。
- 更新参数： 沿着负梯度方向调整参数值，计算下一个点的位置 x k + 1 = x k ? α k ? f ( x k ) \mathbf{x}_{k+1} = \mathbf{x}_k - \alpha_k \nabla f(\mathbf{x}_k) xk+1?=xk??αk??f(xk?)，其中 α k \alpha_k αk? 是步长（学习率）。
- 重复迭代： 重复步骤 2 和步骤 3，直到满足收敛条件或达到迭代次数上限。
最速下降法的步骤通常是沿着梯度方向最陡峭的下降方向更新参数。但它不一定能够最快地搜索到最优解。这是因为最速下降法可能会受到以下几个限制或问题的影响：
- 初始点选择：若初始点选择不当，可能会导致收敛到局部最优解而非全局最优解。
- 学习率的选取：学习率过大或过小都可能导致算法的性能不佳。过大的学习率可能导致振荡或错过最优解，而过小的学习率会导致收敛速度慢。
- 目标函数的形状：在目标函数非凸或存在高度不规则的情况下，最速下降法可能陷入局部最优解，而无法到达全局最优解。
在存在这些问题的情况下，可以考虑使用其他更高效的优化算法，例如：
- 牛顿法和拟牛顿法：这些方法利用了目标函数的二阶导数信息，能够更快地收敛，并且对于某些情况下，能够避免最速下降法所遇到的问题。
- 启发式算法：使用模拟退火算法、遗传算法等启发式算法可以消除局部最优点的影响。也可以在启发式算法结果的基础上进一步做基于梯度的精确优化算法。
- 多起点局部优化：选择多个初始点，分别基于这些初始点进行优化。
因此，最速下降法并不总是能够最快搜索到最优解，特别是在目标函数复杂、非凸或存在不良条件数的情况下。针对不同的问题，需要综合考虑目标函数的特性，并根据实际情况选择合适的优化算法。
优化算法的选择、停止准则
算法选择
- 目标函数和约束都是线性的：单纯形法或者内点法（变量或者约束个数>1000）
- 目标函数二次的（凸）线性约束：改进的单纯形法或者内点法
- 目标函数和约束都是凸的：椭圆法、割平面法、内点法
- 有多个局部极小点:多初始值优化、模拟退火算法、遗传算法
- 非线性、非凸优化、无约束：Levenberg-Marquardt 、Newton、quasi-Newton 、steepest descent、 Powell’s perpendicular method (or Nelder-Mead)
- 非线性、非凸优化、有约束：
- 等式约束:elimination, Lagrange method
- 线性约束:gradient projection or SQP
- 非线性约束:SQP,or penalty or barrier function
停止准则
- 单纯形法:可以在有限步迭代内收敛
- 凸优化算法:
∣ f ( x ? ) ? f ( x k ) ∣ ? ε f , g ( x k ) ? ε g ∥ x ? ? x k ∥ 2 ? ε x ?(for?ellipsoid)? \begin{aligned} \left|f\left(x^*\right)-f\left(x_k\right)\right| & \leqslant \varepsilon_f, \quad g\left(x_k\right) \leqslant \varepsilon_g \\ \left\|x^*-x_k\right\|_2 & \leqslant \varepsilon_x \quad \text { (for ellipsoid) } \end{aligned} ∣f(x?)?f(xk?)∣∥x??xk?∥2???εf?,g(xk?)?εg??εx??(for?ellipsoid)?? - 无约束非线性优化: ∥ ? f ( x k ) ∥ 2 ? ε ? \left\|\nabla f\left(x_k\right)\right\|_2 \leqslant \varepsilon_{\nabla} ∥?f(xk?)∥2??ε??
- 有约束非线性优化:
∥ ? f ( x k ) + ? g ( x k ) μ + ? h ( x k ) λ ∥ 2 ? ε K T , 1 ∣ μ T g ( x k ) ∣ ? ε K T , 2 μ ? ? ε K T , 3 ∥ h ( x k ) ∥ 2 ? ε K T , 4 g ( x k ) ? ε K T , 5 \begin{aligned} \left\|\nabla f\left(x_k\right)+\nabla g\left(x_k\right) \mu+\nabla h\left(x_k\right) \lambda\right\|_2 & \leqslant \varepsilon_{\mathrm{KT}, 1} \\ \left|\mu^T g\left(x_k\right)\right| & \leqslant \varepsilon_{\mathrm{KT}, 2} \\ \mu & \geqslant-\varepsilon_{\mathrm{KT}, 3} \\ \left\|h\left(x_k\right)\right\|_2 & \leqslant \varepsilon_{\mathrm{KT}, 4} \\ g\left(x_k\right) & \leqslant \varepsilon_{\mathrm{KT}, 5} \end{aligned} ∥?f(xk?)+?g(xk?)μ+?h(xk?)λ∥2? ?μTg(xk?) ?μ∥h(xk?)∥2?g(xk?)??εKT,1??εKT,2???εKT,3??εKT,4??εKT,5?? - 模拟退火、遗传算法:达到最大迭代次数。
例题
max
?
x
∈
R
3
4
x
1
+
5
x
2
?
6
x
3
?s.t.?
log
?
∣
2
x
1
+
7
x
2
+
5
x
3
∣
?
1
x
1
,
x
2
,
x
3
?
0
\begin{aligned} & \max _{x \in \mathbb{R}^3} 4 x_1+5 x_2-6 x_3 \\ & \text { s.t. } \log \left|2 x_1+7 x_2+5 x_3\right| \leqslant 1 \\ & x_1, x_2, x_3 \geqslant 0 \\ \end{aligned}
?x∈R3max?4x1?+5x2??6x3??s.t.?log∣2x1?+7x2?+5x3?∣?1x1?,x2?,x3??0?
约束可以逐步简化
先简化为
∣
2
x
1
+
7
x
2
+
5
x
3
∣
?
e
\left|2 x_1+7 x_2+5 x_3\right| \leqslant e
∣2x1?+7x2?+5x3?∣?e
在简化为
2
x
1
+
7
x
2
+
5
x
3
?
e
?
2
x
1
?
7
x
2
?
5
x
3
?
e
2 x_1+7 x_2+5 x_3 \leqslant e \\ -2 x_1-7 x_2-5 x_3 \leqslant e
2x1?+7x2?+5x3??e?2x1??7x2??5x3??e
这样约束就变为了一个线性化约束，可以在化为标准型之后用单纯性法求解，也可以用内点法求解。
单纯形法在有限步会求得最终结果，而内点法收敛条件为
∣
f
(
x
?
)
?
f
(
x
k
)
∣
?
ε
f
\left|f\left(x^*\right)-f\left(x_k\right)\right|\leqslant \varepsilon_f
∣f(x?)?f(xk?)∣?εf?
min
?
x
∈
R
3
max
?
(
cosh
?
(
x
1
+
x
2
+
x
3
)
,
(
5
x
1
?
6
x
2
+
7
x
3
+
6
)
2
)
?s.t.?
∥
x
∥
2
?
10
R
e
m
a
r
k
:
cosh
?
x
=
e
x
+
e
?
x
2
\begin{aligned} & \min _{x \in \mathbb{R}^3} \max \left(\cosh \left(x_1+x_2+x_3\right),\left(5 x_1-6 x_2+7 x_3+6\right)^2\right) \\ & \text { s.t. }\|x\|_2 \leqslant 10 \end{aligned} \\Remark: \cosh x=\frac{e^x+e^{-x}}{2}
?x∈R3min?max(cosh(x1?+x2?+x3?),(5x1??6x2?+7x3?+6)2)?s.t.?∥x∥2??10?Remark:coshx=2ex+e?x?
问题仍然可以做简化令
t
>
=
cosh
?
(
x
1
+
x
2
+
x
3
)
t
>
=
(
5
x
1
?
6
x
2
+
7
x
3
+
6
)
2
t >= \cosh \left(x_1+x_2+x_3\right)\\ t>=\left(5 x_1-6 x_2+7 x_3+6\right)^2
t>=cosh(x1?+x2?+x3?)t>=(5x1??6x2?+7x3?+6)2化为
min
?
x
∈
R
3
t
?s.t.?
∥
x
∥
2
?
10
t
>
=
cosh
?
(
x
1
+
x
2
+
x
3
)
t
>
=
(
5
x
1
?
6
x
2
+
7
x
3
+
6
)
2
\begin{aligned} & \min _{x \in \mathbb{R}^3} t \\ & \text { s.t. }\|x\|_2 \leqslant 10\\ & t >= \cosh \left(x_1+x_2+x_3\right)\\& t>=\left(5 x_1-6 x_2+7 x_3+6\right)^2 \end{aligned}
?x∈R3min?t?s.t.?∥x∥2??10t>=cosh(x1?+x2?+x3?)t>=(5x1??6x2?+7x3?+6)2?
问题变为了常见的含约束凸优化问题，可以用切平面法、椭球法、内点法
收敛条件:
∣
f
(
x
?
)
?
f
(
x
k
)
∣
?
ε
f
,
g
(
x
k
)
?
ε
g
∥
x
?
?
x
k
∥
2
?
ε
x
?(for?ellipsoid)?
\begin{aligned} \left|f\left(x^*\right)-f\left(x_k\right)\right| & \leqslant \varepsilon_f, \quad g\left(x_k\right) \leqslant \varepsilon_g \\ \left\|x^*-x_k\right\|_2 & \leqslant \varepsilon_x \quad \text { (for ellipsoid) } \end{aligned}
∣f(x?)?f(xk?)∣∥x??xk?∥2???εf?,g(xk?)?εg??εx??(for?ellipsoid)??
max
?
x
∈
R
2
e
?
x
1
2
?
x
2
2
(
x
1
2
+
x
1
x
2
+
6
x
1
)
\max _{x \in \mathbb{R}^2} e^{-x_1^2-x_2^2}\left(x_1^2+x_1 x_2+6 x_1\right)
x∈R2max?e?x12??x22?(x12?+x1?x2?+6x1?)
无约束非线性问题，用LM，牛顿法，那几种共轭梯度法，最速下降法，方向+一维搜索法，NM法等
LM，牛顿法，那几种共轭梯度法，最速下降法，方向+一维搜索法收敛条件:
∥
?
f
(
x
k
)
∥
2
?
ε
?
\left\|\nabla f\left(x_k\right)\right\|_2 \leqslant \varepsilon_{\nabla}
∥?f(xk?)∥2??ε??
NM法收敛条件:
∣
f
(
x
?
)
?
f
(
x
k
)
∣
?
ε
f
,
∥
x
?
?
x
k
∥
2
?
ε
x
\begin{aligned} \left|f\left(x^*\right)-f\left(x_k\right)\right| & \leqslant \varepsilon_f,\\ \left\|x^*-x_k\right\|_2 & \leqslant \varepsilon_x \end{aligned}
∣f(x?)?f(xk?)∣∥x??xk?∥2???εf?,?εx??
max
?
x
∈
R
3
x
1
x
2
x
3
1
+
x
1
6
+
x
2
4
+
x
3
2
?s.t.?
x
1
+
x
2
+
x
3
=
1
\begin{aligned} & \max _{x \in \mathbb{R}^3} \frac{x_1 x_2 x_3}{1+x_1^6+x_2^4+x_3^2} \\ & \text { s.t. } x_1+x_2+x_3=1 \end{aligned}
?x∈R3max?1+x16?+x24?+x32?x1?x2?x3???s.t.?x1?+x2?+x3?=1?
由于有多个局部最优点，使用模拟退火算法、遗传算法、以及多起点优化算法（每个起点可分别用内点法之类的优化算法）。
模拟退火算法、遗传算法在达到最大迭代次数之后算法退出。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- JAVA_LinkedList添加元素源码分析（jdk17）
- 记录：零基础小白初学云计算 第五天
- vscode 同步插件
- C# 中，在字符串中设置变量
- L1-077 大笨钟的心情(Java)
- GBASE南大通用数据库分享访问多个数据库的 SQL 语句
- 【Vue原理解析】之虚拟DOM
- 【LeetCode】20. 有效的括号（简单）——代码随想录算法训练营Day11
- 链表存数相加算法(leetcode第2题)
- P1115 最大子段和