面试算法90:环形房屋偷盗
发布时间:2024年01月04日
题目
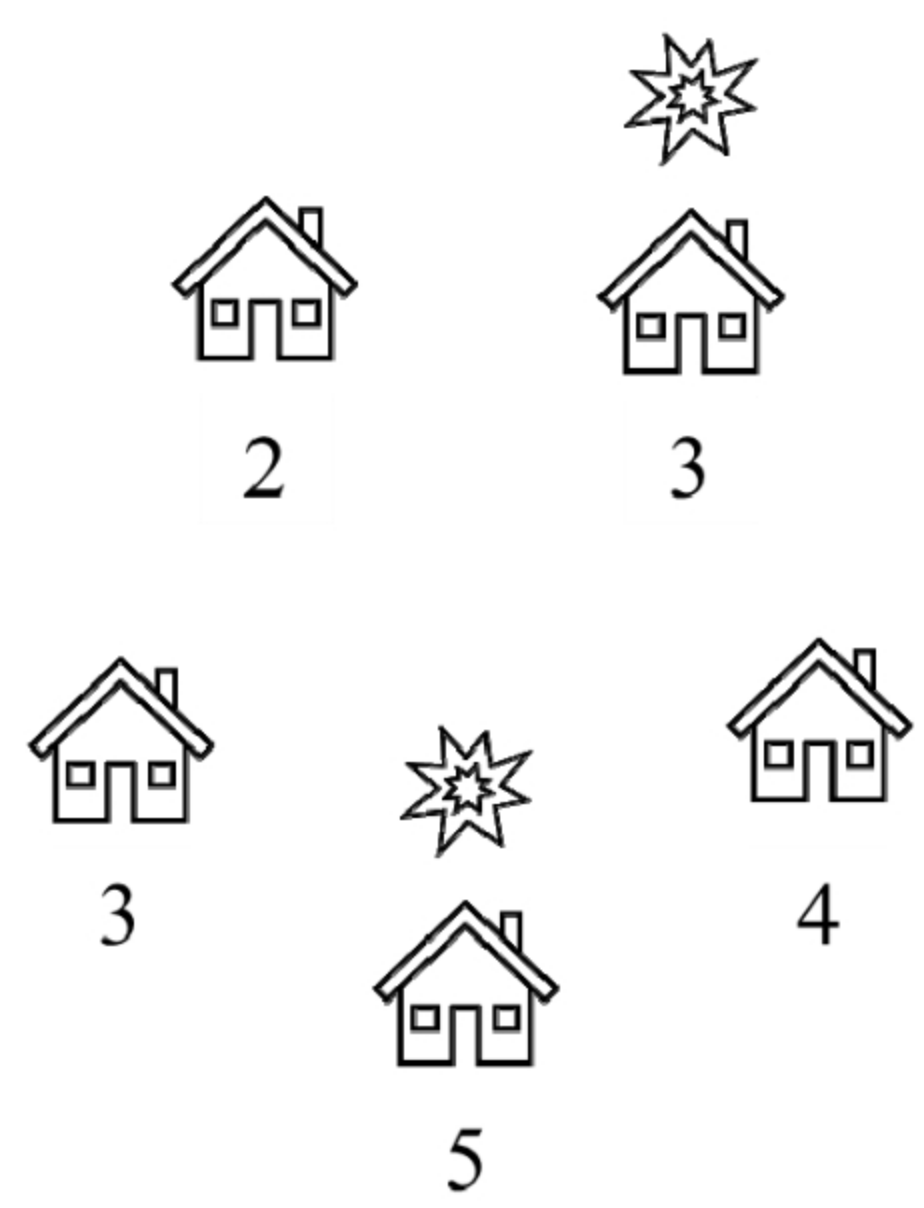
一条环形街道上有若干房屋。输入一个数组表示该条街道上的房屋内财产的数量。如果这条街道上相邻的两幢房屋被盗就会自动触发报警系统。请计算小偷在这条街道上最多能偷取的财产的数量。例如,街道上5家的财产用数组[2,3,4,5,3]表示,如果小偷到下标为1和3的房屋内盗窃,那么他能偷取到价值为8的财物,这是他在不触发报警系统的情况下能偷取到的最多的财物
分析
由于这个问题和面试题89的区别在于小偷不能同时到标号为0和n-1的两幢房屋内偷东西。如果他考虑去标号为0的房屋,那么他一定不能去标号为n-1的房屋;如果他考虑去标号为n-1的房屋,那么他一定不能去标号为0的房屋。因此,可以将这个问题分解成两个子问题:一个问题是求小偷从标号为0开始到标号为n-2结束的房屋内能偷得的最多财物数量,另一个问题是求小偷从标号为1开始到标号为n-1结束的房屋内能偷得的最多财物数量。小偷从标号为0开始到标号为n-1结束的房屋内能偷得的最多财物数量是这两个子问题的解的最大值。
解
public class Test {
public static void main(String[] args) {
int[] cost = {2, 3, 4, 5, 3};
int result = rob(cost);
System.out.println(result);
}
public static int rob(int[] nums) {
if (nums.length == 0) {
return 0;
}
if (nums.length == 1) {
return nums[0];
}
int result1 = helper(nums, 0, nums.length - 2);
int result2 = helper(nums, 1, nums.length - 1);
return Math.max(result1, result2);
}
private static int helper(int[] nums, int start, int end) {
int[] dp = new int[2];
dp[0] = nums[start];
if (start < end) {
dp[1] = Math.max(nums[start], nums[start + 1]);
}
for (int i = start + 2; i <= end; i++) {
int j = i - start;
dp[j % 2] = Math.max(dp[(j - 1) % 2], dp[(j - 2) % 2] + nums[i]);
}
return dp[(end - start) % 2];
}
}
文章来源:https://blog.csdn.net/GoGleTech/article/details/135387201
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 洛谷P1161 开灯
- 虚拟机安装&配置&winServer2012
- java web项目中的拦截器与过滤器区别及使用场景。
- c++/c对应内存分区
- fiddler根据规则替换本地文件
- 精细经营:为 Web3 游戏长期卓越奠定基石
- LoongArch指令集-特权指令系统——摘抄自胡伟武体系结构
- 用友crm客户关系管理pub/help2.php接口存在任意文件读取漏洞 附POC
- 软件测试卷王2024年第一天就开始卷?
- 刷脸消费进入机关单位、企业员工消费应用场景