Circles of Waiting洛谷黑题题解

Circles of Waiting

题面翻译

在平面直角坐标系上，有一个神奇的点，一开始在 $(0,0)$ 。每秒钟这个点都会随机移动：如果它在 $(x,y)$ ，下一秒它在 $(x?1,y)$ 的概率是 $p_1$ ，在 $(x,y?1)$ 的概率是 $p_2$ ，在 $(x+1,y)$ 的概率是 $p_3$ ，在 $(x,y+1)$ 的概率是 $p_4$ 。保证 $p_1+p_2+p_3+p_4=1$ ，各次移动互不关联。

求出这个点移动至距离原点距离为大于 $R$ 的点的期望步数。距离为欧几里得距离。

感谢@OrangeLee 提供的翻译

题目描述

A chip was placed on a field with coordinate system onto point $ (0,0) $ .

Every second the chip moves randomly. If the chip is currently at a point $ (x,y) $ , after a second it moves to the point $ (x-1,y) $ with probability $ p_{1} $ , to the point $ (x,y-1) $ with probability $ p_{2} $ , to the point $ (x+1,y) $ with probability $ p_{3} $ and to the point $ (x,y+1) $ with probability $ p_{4} $ . It’s guaranteed that $ p_{1}+p_{2}+p_{3}+p_{4}=1 $ . The moves are independent.

Find out the expected time after which chip will move away from origin at a distance greater than $ R $ (i.e. 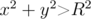will be satisfied).

输入格式

First line contains five integers $ R,a_{1},a_{2},a_{3} $ and $ a_{4} $ ( $ 0<=R<=50,1<=a_{1},a_{2},a_{3},a_{4}<=1000 $ ).

Probabilities $ p_{i} $ can be calculated using formula .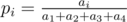

输出格式

It can be shown that answer for this problem is always a rational number of form 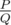, where .

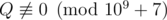Print $ P·Q^{-1} $ modulo $ 10^{9}+7 $ .

样例 #1

样例输入 #1

0 1 1 1 1

样例输出 #1

1

样例 #2

样例输入 #2

1 1 1 1 1

样例输出 #2

666666674

样例 #3

样例输入 #3

1 1 2 1 2

样例输出 #3

538461545

提示

In the first example initially the chip is located at a distance $ 0 $ from origin. In one second chip will move to distance $ 1 $ is some direction, so distance to origin will become $ 1 $ .

Answers to the second and the third tests: and .# Circles of Waiting

题面翻译

在平面直角坐标系上，有一个神奇的点，一开始在 $(0,0)$ 。每秒钟这个点都会随机移动：如果它在 $(x,y)$ ，下一秒它在 $(x?1,y)$ 的概率是 $p_1$ ，在 $(x,y?1)$ 的概率是 $p_2$ ，在 $(x+1,y)$ 的概率是 $p_3$ ，在 $(x,y+1)$ 的概率是 $p_4$ 。保证 $p_1+p_2+p_3+p_4=1$ ，各次移动互不关联。

求出这个点移动至距离原点距离为大于 $R$ 的点的期望步数。距离为欧几里得距离。

感谢@OrangeLee 提供的翻译

题目描述

A chip was placed on a field with coordinate system onto point $ (0,0) $ .

Every second the chip moves randomly. If the chip is currently at a point $ (x,y) $ , after a second it moves to the point $ (x-1,y) $ with probability $ p_{1} $ , to the point $ (x,y-1) $ with probability $ p_{2} $ , to the point $ (x+1,y) $ with probability $ p_{3} $ and to the point $ (x,y+1) $ with probability $ p_{4} $ . It’s guaranteed that $ p_{1}+p_{2}+p_{3}+p_{4}=1 $ . The moves are independent.

Find out the expected time after which chip will move away from origin at a distance greater than $ R $ (i.e. 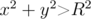will be satisfied).

输入格式

First line contains five integers $ R,a_{1},a_{2},a_{3} $ and $ a_{4} $ ( $ 0<=R<=50,1<=a_{1},a_{2},a_{3},a_{4}<=1000 $ ).

Probabilities $ p_{i} $ can be calculated using formula .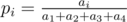

输出格式

It can be shown that answer for this problem is always a rational number of form 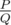, where .

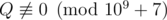Print $ P·Q^{-1} $ modulo $ 10^{9}+7 $ .

样例 #1

样例输入 #1

0 1 1 1 1

样例输出 #1

1

样例 #2

样例输入 #2

1 1 1 1 1

样例输出 #2

666666674

样例 #3

样例输入 #3

1 1 2 1 2

样例输出 #3

538461545

提示

In the first example initially the chip is located at a distance $ 0 $ from origin. In one second chip will move to distance $ 1 $ is some direction, so distance to origin will become $ 1 $ .

Answers to the second and the third tests: and .

题意
在平面直角坐标系上有一个初始在 (0,0)(0,0) 的点，每秒钟这个点都会随机移动 ，求出这个点移动至距离原点欧几里得距离大于 RR 的点的期望时间。

数据范围
0\leqslant R\leqslant500?R?50，0\leqslant p1,p2,p3,p40?p1,p2,p3,p4 ，答案对 10^9+710 9+7取模

分析
wxh论文中的例题。

本题有两种方法，O(R^4)O(R 4) 的直接消元和 O(R^3)O(R 3) 的主元法，本文主要介绍第二种方法。

设 f(i,j)f(i,j) 表示从 (i,j)(i,j) 出发走出圈的期望步数，那么根据题意，有：

对于在圈外面的点 f(i,j)=0f(i,j)=0。

这样就可以高斯消元做了，但由于方程数是 O(R^2)O(R 2 ) 的，朴素实现复杂度为 O(R^6)O(R 6 )，无法通过此题。

注意到原图为网格图，那么只要钦定一个方向和一组初始点的 ff 作为主元，就可以把所有的点的 ff 用主元表示出来，最后通过圈外点 f=0f=0 列方程，解出初始点的 ff 值，带入 f(0,0)f(0,0) 求解即可。

具体实现上钦定方向从左到右，将每行从左到右第一个点作为主元，共 2R+12R+1 个。转移到一个点时，其左边的点都是已知的，

这就可以直接转移了,转移到某个圈外点时就得到一个方程 f(i+1,j)=0f(i+1,j)=0，最后有 2*R+12?R+1 个未知数和方程，高斯消元的复杂度就降为 O(R^3)O(R 3)了。

代码
代码中为了方便使用优先队列来保证左边的点先被转移，不过不影响复杂度。

#include<bits/stdc++.h>
#define Mod 1000000007
#define _gc getchar()
#define ll long long
#define FOR(i,a,b) for(register int i=a;i<=b;i++)
#define ROF(i,b,a) for(register int i=b;i>=a;i--) 
using namespace std;
inline int read(){
	int x=0;char s=_gc;
	while('0'>s||s>'9')s=_gc;
	while('0'<=s&&s<='9'){x=x*10+s-48;s=_gc;}
	return x;
}
ll fast(ll x,ll p){ll now=1;while(p){if(p&1)now=now*x%Mod;x=x*x%Mod;p>>=1;}return now;}
ll Inv(ll x){return fast(x,Mod-2);}
const int N=111;
int n,tot;
ll R,a1,a2,a3,a4,Ans,ans[N],b[N][N];
bool book[N*N],Ed[N*N]; 

struct vec{int x,y;friend bool operator < (vec x,vec y){return x.x>y.x;}};
struct node{
	ll a[N];
	friend node operator * (ll x,node y){FOR(i,0,2*R+1)y.a[i]=y.a[i]*x%Mod;return y;}	
	friend node operator + (node y,ll x){y.a[2*R+1]=(y.a[2*R+1]+x)%Mod;return y;}
	friend node operator + (node x,node y){FOR(i,0,2*R+1)x.a[i]=(x.a[i]+y.a[i])%Mod;return x;}	
};
node f[N*N];
priority_queue<vec>q;

void Calc(){
	FOR(i,0,2*R){
		if(!b[i][i]){
			int ok=0;
			FOR(j,i+1,2*R)if(b[j][i]){FOR(k,i,2*R+1)swap(b[i][k],b[j][k]);ok=1;break;}
			if(!ok)return ;
		}
		ll INV=Inv(b[i][i]);
		FOR(j,i+1,2*R){
			ll p=(Mod-b[j][i])*INV%Mod;
			FOR(k,i,2*R+1)b[j][k]=(b[j][k]+p*b[i][k]%Mod+Mod)%Mod;
		}
	}
	ROF(i,2*R,0){
		ans[i]=b[i][2*R+1]*Inv(b[i][i])%Mod;	
		FOR(j,0,i-1)b[j][2*R+1]=(b[j][2*R+1]-ans[i]*b[j][i]%Mod+Mod)%Mod;
	}
}

int mark(int x,int y){return (y+R+1)*n+(x+R+2);}
bool cmp(vec x,vec y){return x.x<y.x;}
int main(){
	R=read(),a1=read(),a2=read(),a3=read(),a4=read();
	n=2*R+3;
	ll p=Inv(a1+a2+a3+a4);
	a1=a1*p%Mod,a2=a2*p%Mod,a3=a3*p%Mod,a4=a4*p%Mod;	
	FOR(i,-R,R)FOR(j,-R,R)if(i*i+j*j<=R*R)book[mark(i,j)]=1;
	FOR(j,-R,R)FOR(i,-R,0)if(book[mark(i,j)]){f[mark(i,j)].a[j+R]=1,q.push(vec{i,j});break;}		
	FOR(j,-R,R)ROF(i,R,-R)if(book[mark(i,j)]){Ed[mark(i+1,j)]=1;break;}
	while(!q.empty()){
		int X=q.top().x,Y=q.top().y;q.pop();	
		if(!book[mark(X+1,Y)]&&!Ed[mark(X+1,Y)])continue;
		f[mark(X+1,Y)]=Inv(a3)*((f[mark(X,Y)]+(Mod-1))+((Mod-a1)*f[mark(X-1,Y)])+((Mod-a2)*f[mark(X,Y-1)])+((Mod-a4)*f[mark(X,Y+1)]));		                   
		if(Ed[mark(X+1,Y)]){
			FOR(i,0,2*R+1)b[Y+R][i]=f[mark(X+1,Y)].a[i];
			b[Y+R][2*R+1]=Mod-b[Y+R][2*R+1];	
		} 
		else q.push(vec{X+1,Y});
	}
	Calc();
	ans[2*R+1]=1;
	FOR(i,0,2*R+1)Ans=(Ans+f[mark(0,0)].a[i]*ans[i]%Mod)%Mod;
	cout<<Ans;
	return 0;
}

/*
0 1 1 1 1

1 1 1 1 1

1 1 2 1 2

20 98 234 546 123

2 235 543 123 432

3 235 543 123 432
*/