1.16 递归（中等)

目录

1.预测赢家（动态规划）

2.第K个语法符号

3.第n个字符串的第k位

4.统计好数字的数目

5.从链表中移除节点

！！链表删减

1.预测赢家（动态规划）

给你一个整数数组?nums?。玩家 1 和玩家 2 基于这个数组设计了一个游戏。

玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手。开始时，两个玩家的初始分值都是?0?。每一回合，玩家从数组的任意一端取一个数字（即，nums[0]?或?nums[nums.length - 1]），取到的数字将会从数组中移除（数组长度减?1?）。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时，游戏结束。

如果玩家 1 能成为赢家，返回?true?。如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回?true?。你可以假设每个玩家的玩法都会使他的分数最大化。

示例 1：

输入：nums = [1,5,2]
输出：false
解释：一开始，玩家 1 可以从 1 和 2 中进行选择。
如果他选择 2（或者 1 ），那么玩家 2 可以从 1（或者 2 ）和 5 中进行选择。如果玩家 2 选择了 5 ，那么玩家 1 则只剩下 1（或者 2 ）可选。 
所以，玩家 1 的最终分数为 1 + 2 = 3，而玩家 2 为 5 。
因此，玩家 1 永远不会成为赢家，返回 false 。

示例 2：

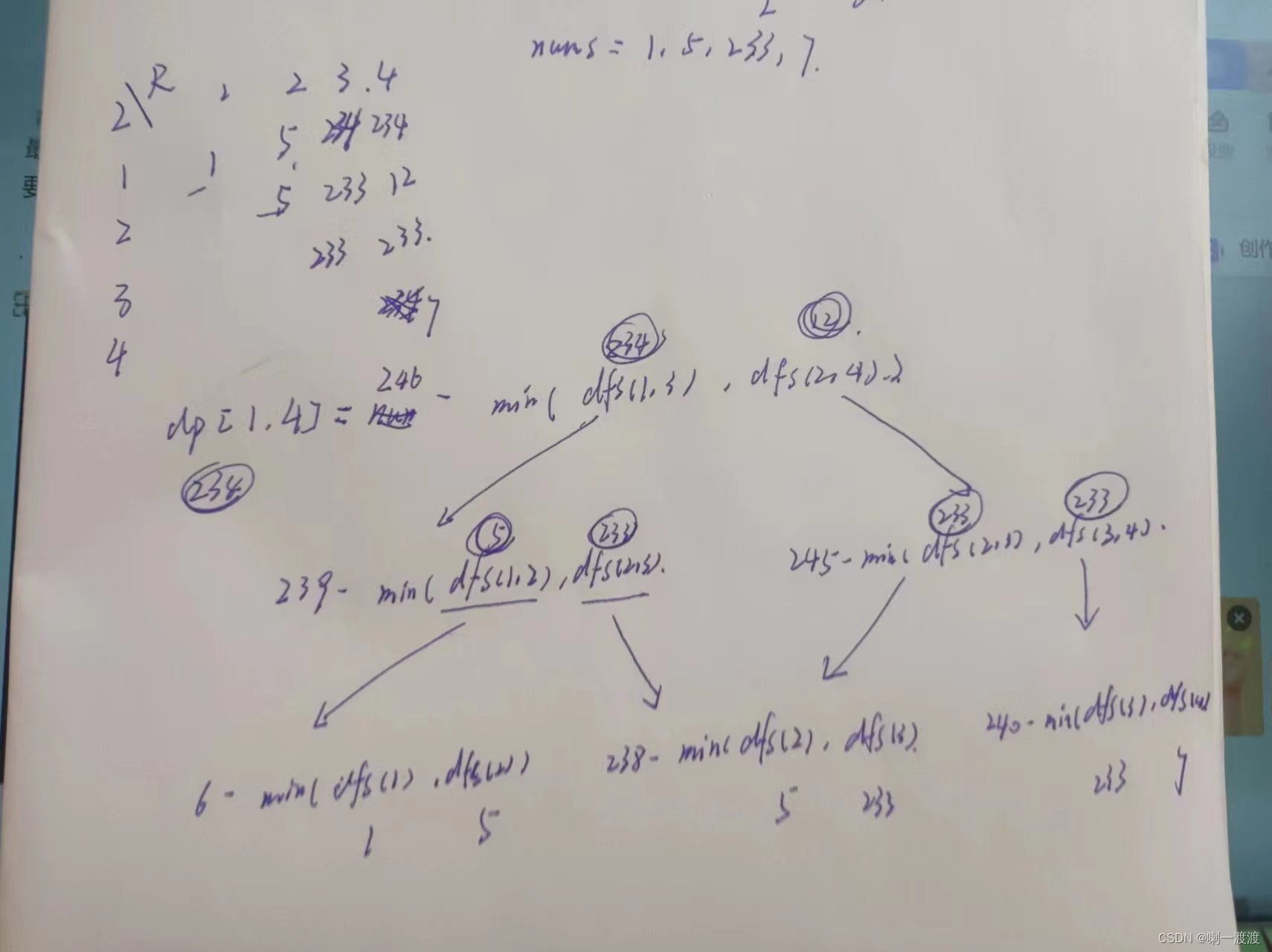
输入：nums = [1,5,233,7]
输出：true
解释：玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个，玩家 1 都可以选择 233 。
最终，玩家 1（234 分）比玩家 2（12 分）获得更多的分数，所以返回 true，表示玩家 1 可以成为赢家。

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 107

分析：在搜到的题解中，管这个问题叫零和博弈，即为无论怎么变化，两者的得分总和不变，所以想让自己的得分最高，就要想办法让对方的得分最小。无论怎样的情况，都会有一个这种情况下的最高得分，所以可以让每一轮的先手控制下一轮的得分最小即可，那当前的得分就是总和减去当前要看的l到r总和最小

. - 力扣（LeetCode）

#include <bits/stdc++.h>

using namespace std;

int dp[21][21];

int sum(const vector<int> &nums,int l,int r)
{
    int sum=0;
    for(int i=l;i<=r;i++)
    {
        sum+=nums[i-1];
    }
    return sum;
}

int dfs(int l,int r,const vector<int> &nums)
{
    if(dp[l][r]!=-1) return dp[l][r];
    if(l==r) return dp[l][r]=nums[l-1];
    return dp[l][r]=sum(nums,l,r)-min(dfs(l+1,r,nums),dfs(l,r-1,nums));
}


bool s(vector<int> &nums)
{
    memset(dp,-1,sizeof(dp));
    return dfs(1,nums.size(),nums)*2>=sum(nums,1,nums.size());
}

main()
{
    vector<int> nums;
    int i=0,x;
    while(cin>>x)
    {
//        cout<<x;
        nums.push_back(x);
 //       cout<<nums[i++]<<" ";
    }
    cout<<endl;
    if(s(nums)) cout<<"true";
    else cout<<"false";


}

2.第K个语法符号

我们构建了一个包含?n?行(?索引从 1? 开始?)的表。首先在第一行我们写上一个?0。接下来的每一行，将前一行中的0替换为01，1替换为10。

• 例如，对于?n = 3?，第?1?行是?0?，第?2?行是?01?，第3行是?0110?。

给定行数?n?和序数?k，返回第?n?行中第?k?个字符。（?k?从索引 1 开始）

示例 1:

输入: n = 1, k = 1
输出: 0
解释: 第一行：0

示例 2:

输入: n = 2, k = 1
输出: 0
解释: 
第一行: 0 
第二行: 01

示例 3:

输入: n = 2, k = 2
输出: 1
解释:
第一行: 0
第二行: 01

提示:

• 1 <= n <= 30
• 1 <= k <= 2n - 1

分析：看到这个题我想到的是队列加双层循环去做，后来看了别人的题解才发现是我草率了，根本用不着这么麻烦，它本身就是有规律的

. - 力扣（LeetCode）

#include <bits/stdc++.h>

using namespace std;


int s(int n,int k)
{
   if(n==1) return 0;
   if(k<= (1<<(n-2))) return s(n-1,k);
   return s(n-1,k-(1<<(n-2)))^1;
}

main()
{
   int n,k;
   cin>>n>>k;
   s(n,k);

}

3.第n个字符串的第k位

给你两个正整数?n?和?k，二进制字符串??Sn?的形成规则如下：

• S1?= "0"
• 当?i > 1?时，Si?=?Si-1?+ "1" + reverse(invert(Si-1))

其中?+?表示串联操作，reverse(x)?返回反转?x?后得到的字符串，而?invert(x)?则会翻转 x 中的每一位（0 变为 1，而 1 变为 0）。

例如，符合上述描述的序列的前 4 个字符串依次是：

• S1?= "0"
• S2?= "011"
• S3?= "0111001"
• S4?= "011100110110001"

请你返回??Sn?的?第?k?位字符?，题目数据保证?k?一定在?Sn?长度范围以内。

示例 1：

输入：n = 3, k = 1
输出："0"
解释：S3 为 "0111001"，其第 1 位为 "0" 。

示例 2：

输入：n = 4, k = 11
输出："1"
解释：S4 为 "011100110110001"，其第 11 位为 "1" 。

示例 3：

输入：n = 1, k = 1
输出："0"

示例 4：

输入：n = 2, k = 3
输出："1"

提示：

• 1 <= n <= 20
• 1 <= k <= 2n - 1

分析：这个和第二题很像，只是处理起来要多处理一下中间的1和后面的reverse

#include <bits/stdc++.h>

using namespace std;


int s(int n,int k)
{
    if(n==1) return 0;
    if(k==(1<<(n-1))) return 1;
    else if(k<(1<<(n-1))) s(n-1,k);
    else return s(n-1,2*(1<<(n-1))-k)^1;
}

main()
{
   int n,k;
   cin>>n>>k;
   cout<<s(n,k);

}

4.统计好数字的数目

我们称一个数字字符串是?好数字?当它满足（下标从?0?开始）偶数?下标处的数字为?偶数?且?奇数?下标处的数字为?质数?（2，3，5?或?7）。

• 比方说，"2582"?是好数字，因为偶数下标处的数字（2?和?8）是偶数且奇数下标处的数字（5?和?2）为质数。但?"3245"?不是?好数字，因为?3?在偶数下标处但不是偶数。

给你一个整数?n?，请你返回长度为?n?且为好数字的数字字符串?总数?。由于答案可能会很大，请你将它对?10^9 + 7?取余后返回?。

一个?数字字符串?是每一位都由?0?到?9?组成的字符串，且可能包含前导 0 。

示例 1：

输入：n = 1
输出：5
解释：长度为 1 的好数字包括 "0"，"2"，"4"，"6"，"8" 。

示例 2：

输入：n = 4
输出：400

示例 3：

输入：n = 50
输出：564908303

提示：

• 1 <= n <= 1015

分析：n个数字的偶数下标有五种取值可能，奇数下标有四种取值可能，我们只要用快速取幂发把他们分别做出来即可

#include <bits/stdc++.h>

using namespace std;

long long mod=1000000007;
long long s(long long a,long long b)
{
    long long res=1;
    while(b)
    {
        if(b%2==1)
        {
            b--;
            res=res*a%mod;
        }
        a=a*a%mod;
        b=b/2;
        cout<<a<<" "<<b<<" "<<endl;

    }
    return res;
}


main()
{
    long long n,a,b;
    cin>>n;
    if(n%2==0) a=n/2;
    else a=n/2+1;
    b=n/2;
//    cout<<a<<" "<<b<<" "<<endl;
  cout<<(s(5,a)%mod)*(s(4,b)%mod)%mod;
    //cout<<(s(5,a)%mod);
}

5.从链表中移除节点

！！链表删减

给你一个链表的头节点?head?。

移除每个右侧有一个更大数值的节点。

返回修改后链表的头节点?head?。

示例 1：

输入：head = [5,2,13,3,8]
输出：[13,8]
解释：需要移除的节点是 5 ，2 和 3 。
- 节点 13 在节点 5 右侧。
- 节点 13 在节点 2 右侧。
- 节点 8 在节点 3 右侧。

示例 2：

输入：head = [1,1,1,1]
输出：[1,1,1,1]
解释：每个节点的值都是 1 ，所以没有需要移除的节点。
提示：

• 给定列表中的节点数目在范围?[1, 105]?内
• 1 <= Node.val <= 105

分析：运用递归，找到最大的，接到后面就好了

但是链表果然是最难写的，重点就是要传入head的首地址，这样head的变化会影响到head1的变化，因为这个知识点写了好久

#include <bits/stdc++.h>

using namespace std;

typedef struct node
{
    int data;
    struct node *next;
};

node* s(node *phead,node * &head)
{
    node *t=new node;
    node *p=new node;
    p=phead->next;
    t->data=-1;
 //   cout<<"1################"<<endl;
    while(p)
    {
 //       cout<<"2################"<<endl;
        if(p->data > t->data)
        {

            phead->next=p;
            t->data=p->data;
            t->next=p->next;
 //           cout<<"3################"<<" "<<p->data<<" "<<t->data<<endl;
        }
        p=p->next;
    }
    phead=t;
    head->next=phead;
    head=head->next;
    node *q=new node;
    if(phead->next!=NULL) return s(phead,head);


}
main()
{
    node *head=new node;
    node *head1=new node;
    node *q=new node;
    int x;
    q=head;
    while(cin>>x)
    {
        node *p=new node;
        p->data=x;
        p->next=NULL;
        q->next=p;
        q=q->next;

    }
    head1=head;
    s(head,head);

    q=head1->next;
    while(q)
    {
        cout<< q->data <<" ";
        q=q->next;
    }

}