每日一题 2866. 美丽塔 II(中等,单调栈)
发布时间:2023年12月21日

- 理解题目意思,希望构建一个数组,该数组的最大值的两边依次单调递减,形成一个峰值,且该数组每个下标对应的值的大小是有上限的
- 显然可以分为两部分求解,因为最大值的左半部分和右半部分是不相干的,因此我们只要找到所有下标的左右两半的最大值,再求和找总的最大值即可,而左右两半的求解方式显然是类似的,下面解释左半最大值的解法
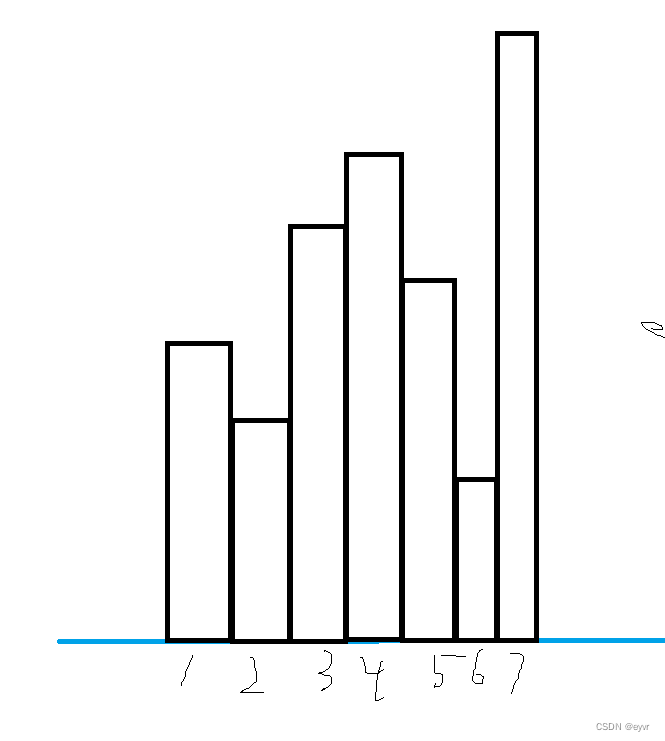
- 抽象法,如下图所示,构建一个以下标所能形成的最大值为值的数组,我们可以清楚地看到如果以下标 7 为峰值,那么不管 6 之前的值有多大,所有的值都只能取到 6 对应的值。或者说在 6 之前的值就只与 6 的峰值有关了,根 7 没有关系了;如果以下标 5 为峰值,那么它的左边一开始是比它大的,这些都能够取到 5 的峰值,然后直到下标 2 比 5 的峰值小,接下来与 5 也无关了总结;总之,当以下标 i 为峰值时,先寻找它左边的最长比它大序列,这些都是取 i 的峰值的,在这之后的取值就与 i 无关了,应当是当以下标 t 为峰值时(下标 t 则是第一个比 i 的峰值小的下标),左半部分的取值和的最大值
- 右半部分同理可求,代码实现需要对每一个 i 寻找它两边的最长比它大序列,然后把两边加起来求最大值,如果最长比它大序列采用遍历的方式,其时间复杂度为O(n2),现在我们需要找到一个更好的来最长比它大序列的方法
- 由步骤 3 我们可以知道,例如下标 6,不管1,2,3,4,5对应的峰值有多大,都无法影响到之后的下标的取值,因此采用单调栈的思想,当下标 6 入栈时,弹出所有比 6 的峰值更大的下标,这些下标都被 6 的峰值限制了;再看到对于下标 5 而言,弹出 3,4之后,遇到栈中第一个比它小的下标 2,此时就和步骤3的结论一样,下标 5 对应的左半部分的最大值就是弹出栈的元素的数量乘以 5 的峰值,再加上此时栈顶元素对应左半部分最大值
- 由步骤 5 我们可以以总体 O(n) 的时间复杂度来求解找到一个更好的来最长比它大序列,因为每个下标智慧出栈入栈一次
- 最后右半部分同样的处理,然后求和取最大值求解
class Solution:
def maximumSumOfHeights(self, maxHeights: List[int]) -> int:
n = len(maxHeights)
leftm, rightm = [0] * n, [0] * n
leftm[0] = maxHeights[0]
rightm[n - 1] = maxHeights[n - 1]
st = [0]
for i in range(1, n):
while len(st) > 0 and maxHeights[i] < maxHeights[st[-1]]:
st.pop()
leftm[i] = (leftm[st[-1]] + maxHeights[i] * (i - st[-1])) if len(st) > 0 else maxHeights[i] * (i + 1)
st.append(i)
st = [n - 1]
for i in range(n - 2, -1, -1):
while len(st) > 0 and maxHeights[i] <= maxHeights[st[-1]]:
st.pop()
rightm[i] = (rightm[st[-1]] + maxHeights[i] * (st[-1] - i)) if len(st) > 0 else maxHeights[i] * (n - i)
st.append(i)
return max([rightm[i] + leftm[i] - maxHeights[i] for i in range(n)])
文章来源:https://blog.csdn.net/qq_46636391/article/details/135134002
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 基于ssm校园体育赛事管理系统的设计与实现论文
- 算法34:贴纸拼词(力扣691题)
- 05. 深入理解 GPT 架构
- C语言入门到精通之练习十一:古典问题(兔子生崽)
- 设计模式之建造者模式
- Vue中插槽的简单使用
- YOLOv8优化策略:轻量化改进 | 华为GhostNet再升级,全系列硬件上最优极简AI网络G_ghost | IJCV22
- 『C++成长记』模板
- 「Qt Widget中文示例指南」如何实现一个日历?(三)
- 【从3D点云生成平面图:一种空间划分方法】