初级数据结构（六）——堆
| ?????文中代码源文件已上传：数据结构源码 <-上一篇 初级数据结构（五）——树和二叉树的概念? ? ? ? |????????NULL 下一篇-> |
1、堆的特性
1.1、定义
? ? ? ? 堆结构属于完全二叉树的范畴，除了满足完全二叉树的限制之外，还满足所有父节点数据的值均大于（或小于）子节点。
? ? ? ? 父节点大于子节点的堆称为大堆或大根堆，反之则称为小堆或小根堆。
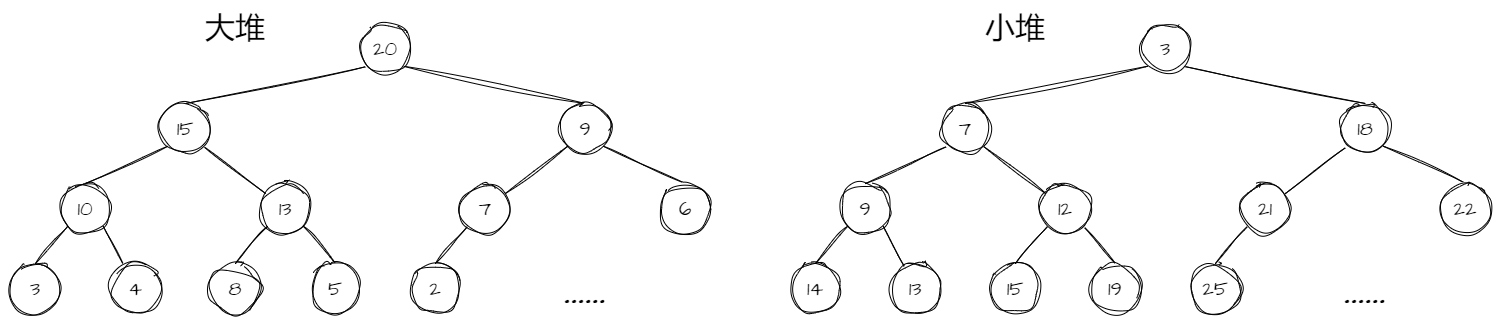
? ? ? ? 下面例子由于红色节点不符合堆的定义，所以不是堆。
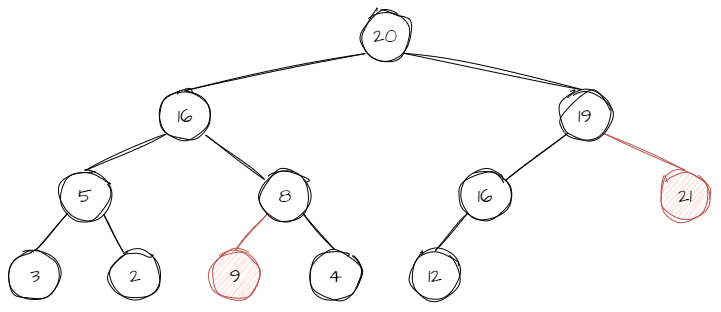
1.2、实现方式
? ? ? ? 由于堆每插入一个数据，它的位置是确定的，所以一般都是以顺序表构建堆，插入新节点只相当于顺序表的尾插。这个顺序表与本系列第一篇里定义的顺序表可以说完全一样，区别只在于对表的操作上。当然你也可以用二叉节点或者三叉节点来创建堆，但这样一来后续对堆的操作会特别繁琐。
? ? ? ? 在这里，需要重点理解，以顺序表来创建堆其实际结构是线性的，但我们通过对下标序号附以一定意义，把它抽象成树结构。
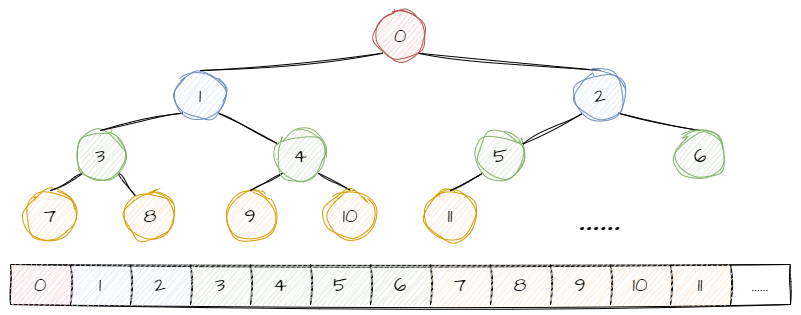
????????访问顺序我们可以先回顾上一篇里的两张图：
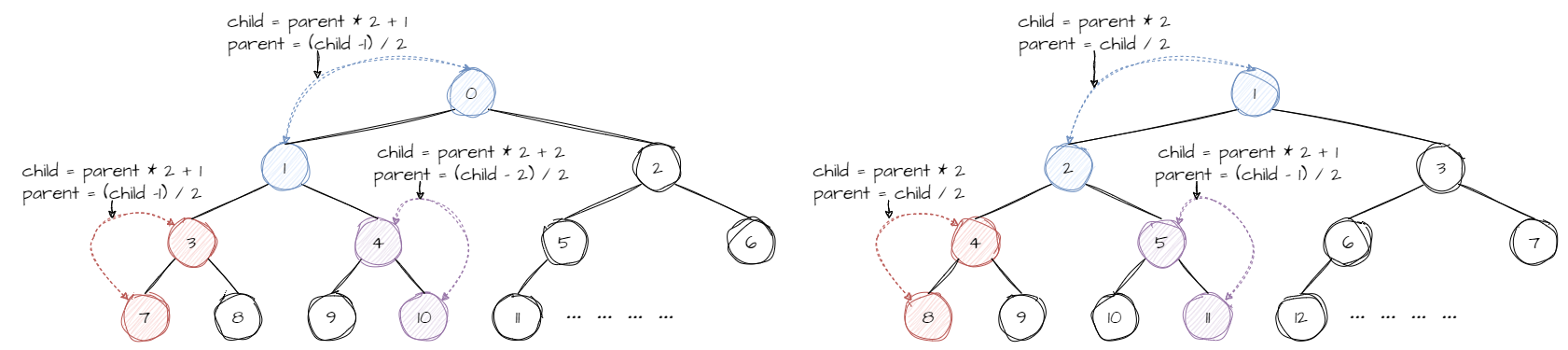
????????顺序表第一个元素下标为 0 ，我们以它作为根节点，子节点在顺序表中的下标分别是父节点下标的二倍 +1 和二倍 +2 。
size_t child_1 = parent * 2 + 1;
size_t child_2 = parent * 2 + 2;
size_t parent = (child_1 - 1) / 2;
size_t parent = (child_2 - 1) / 2;? ? ? ? 若取下标为 1 的位置作为根节点的情况下（ 0 的位置空置即可），子节点在顺序表中的下标分别是父节点下标的二倍和二倍 +1 。
size_t child_1 = parent * 2;
size_t child_2 = parent * 2 + 1;
size_t parent = child_1 / 2;
size_t parent = child_2 / 2;2、堆构建
2.1、文件结构
? ? ? ? 以顺序表的方式构建堆，这次选用柔性数组的结构体形式。与之前相同的三个文件：
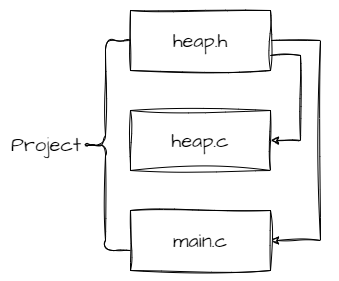
?? ? ? ?heap.h ：用于创建项目的结构体类型以及声明函数；
? ? ? ? heap.c ：用于创建堆各种操作功能的函数；
? ? ? ? main.c ：仅创建?main 函数，用作测试。
2.2、前期工作
? ? ? ? heap.h 中内容如下。这里需要注意的是，由于堆是以 malloc 形式创建的空间，以指针记录，销毁堆的函数最终需要把该指针变量置空，所以需要传指针的地址。而插入数据和删除数据由于涉及 realloc ，有异地扩容的可能，同样需要改变堆指针记录的地址，所以这三个函数参数都必须定义为二级指针：
#include <stdio.h>
#include <stdlib.h>
//大堆大于号 小堆小于号
#define COMPARE <
//存储数据类型的定义及打印占位符预定义
#define DATAPRT "%d"
typedef int DATATYPE;
//堆结构体类型
typedef struct Heap
{
size_t size; //记录堆内数据个数
size_t capacity; //记录已开辟空间大小
DATATYPE data[0]; //数据段
}Heap;
//函数声明-----------------------------------
//创建堆
extern Heap* HeapCreate();
//销毁堆
extern void HeapDestroy(Heap**);
//插入数据
extern void HeapPush(Heap**, DATATYPE);
//删除数据
extern void HeapPop(Heap**);? ? ? ? 然后是 heap.c ：
#include "heap.h"
//创建堆
Heap* HeapCreate()
{
//创建堆空间
Heap* heap = (Heap*)malloc(sizeof(Heap) + sizeof(DATATYPE) * 4);
//创建结果检查
if (!heap)
{
fprintf(stderr, "Malloc Fail\n");
return NULL;
}
//初始化储存记录
heap->size = 0;
heap->capacity = 4;
return heap;
}
//销毁堆
void HeapDestroy(Heap** heap)
{
//堆地址有效性检查
if (!heap || !*heap)
{
fprintf(stderr, "Heap Address NULL\n");
return;
}
//销毁堆空间
free(*heap);
*heap = NULL;
}? ? ? ? 这次就不每一步都测试了，构建过程中可以自行测试。所以只需要在 main.c 中写入 include 头文件和 main 函数的壳即可：
#include "heap.h"
int main()
{
return 0;
}3、堆的数据操作
? ? ? ? 由于堆的特性，主要只涉及增加数据及删除数据两个功能查找和修改在堆的操作上没有意义。此外，本节的全部代码均写在 heap.c 之中。
3.1、插入数据
? ? ? ? 插入数据实际上是对顺序表的尾插，但是尾插之后的堆很可能不符合堆的定义，因此，尾插之后还需对堆进行调整。调整步骤是不断地将插入的数据与父节点进行比较，如果不符合大堆或者小堆的规律，则互换。
? ? ? ? 这种操作称作向上调整，也叫做上滤。以下是上滤操作的代码，由于只在 heap.c 中调用，用 static 修饰比较好。
//上滤
static void HeapFilterUp(Heap* heap)
{
//堆地址有效性检查
if (!heap)
{
fprintf(stderr, "Heap Address NULL\n");
return NULL;
}
//获取初始父节点子节点下标
size_t child = heap->size - 1;
size_t parent = (child - 1) / 2;
while (child != 0)
{
//如果不满足堆的条件
if (heap->data[child] COMPARE heap->data[parent])
{
//向上交换数据
DATATYPE tempData = heap->data[child];
heap->data[child] = heap->data[parent];
heap->data[parent] = tempData;
//计算新的父子节点下标
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}? ? ? ? 上滤函数中有两个比较容易坑的点，首先是循环条件应该是子节的位置作为判断依据，当子节点下标为 0 时说明已经到根节点了，至此中断循环。此外，当交换到某个位置时已经满足堆的特性，记得中断循环。
????????完成上滤函数之后就可以开始写插入数据的函数主体了：
//插入数据
void HeapPush(Heap** ptr_heap, DATATYPE data)
{
//堆地址有效性检查
if (!ptr_heap || !*ptr_heap)
{
fprintf(stderr, "Heap Address NULL\n");
return;
}
//空间不足则扩容
if ((*ptr_heap)->size >= (*ptr_heap)->capacity)
{
Heap* tempHeap = NULL;
while (!tempHeap)
{
tempHeap = (Heap*)realloc(*ptr_heap, sizeof(Heap) + sizeof(DATATYPE) * (*ptr_heap)->capacity * 2);
}
*ptr_heap = tempHeap;
(*ptr_heap)->capacity *= 2;
}
//数据插入堆尾
(*ptr_heap)->data[(*ptr_heap)->size] = data;
(*ptr_heap)->size++;
//上滤
HeapFilterUp(*ptr_heap);
}3.2、删除数据
? ? ? ? 这部分有点像由顺序表构建的队列（ FIFO 属性）。堆删除数据总是删除根节点。但是删除根节点后，并不能如队列般将后面的元素往前挪，原因如下图：
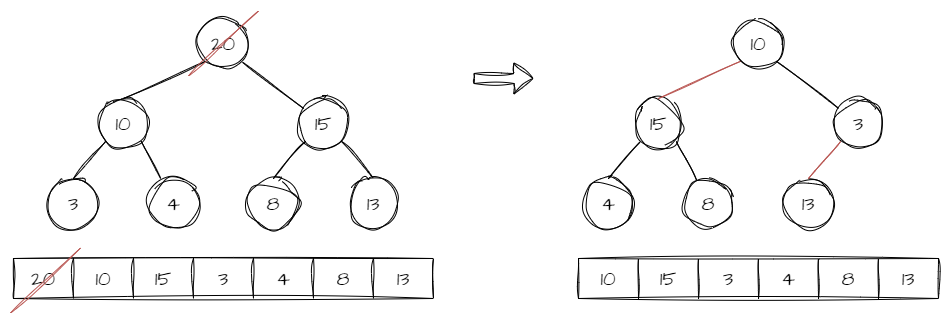
? ? ? ? 因为堆的顺序与队列的顺序不一样，既然是堆，则不能以队列的方式挪动数据。
????????堆删除数据的常规的方式是将最后一个节点覆盖到根节点，然后将 size - 1 。之后与上滤类似，堆挪动数据的方式称为下滤或向下调整。过程是：先比较两个子节点的大小，如果是大堆，则取较大的子节点，再以较大的子节点与父节点比较，如果不符合堆的特性，则两者互换，一直到叶节点。具体看下图例子。
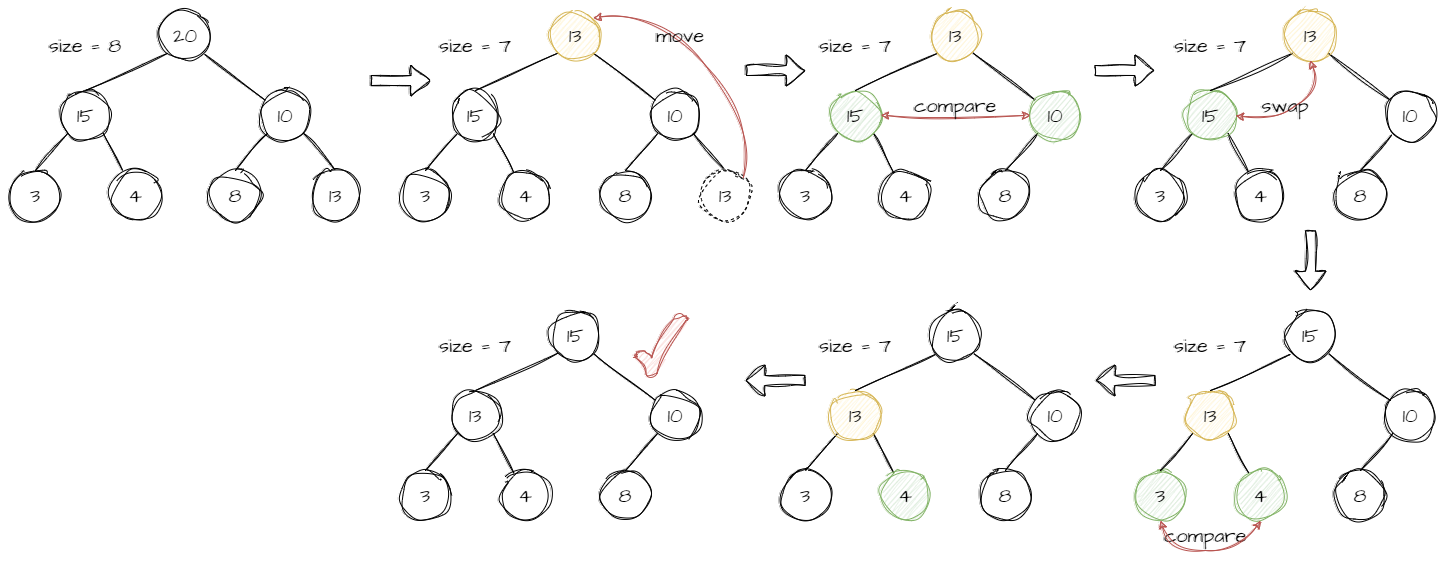
? ? ? ? ?根据这个思路，先凹一个下滤函数：
//下滤
static void HeapFilterDown(Heap* heap)
{
//堆地址有效性检查
if (!heap)
{
fprintf(stderr, "Heap Address NULL\n");
return NULL;
}
//获取初始父节点子节点下标
size_t parent = 0;
size_t child = 1;
while (child < heap->size)
{
//将左右两个子节点中数据较大值的节点下标赋予child
if (child + 1 < heap->size && heap->data[child + 1] COMPARE heap->data[child])
{
child++;
}
//如果不满足堆的条件
if (heap->data[child] COMPARE heap->data[parent])
{
//向下交换数据
DATATYPE tempData = heap->data[child];
heap->data[child] = heap->data[parent];
heap->data[parent] = tempData;
//计算新的父子节点下标
parent = child;
child = child * 2 + 1;
}
else
{
break;
}
}
}? ? ? ? 刚才写完上滤函数之后，写下滤函数最容易入一个坑就是循环条件以父节点下标是否超过数据个数作判定，但当父节点为叶节点时，子节点下标便已经超过数据个数了。当然也可以以父节点是否有子节点判定，但本质上，这还是判定子节点。
? ? ? ? 此外还有一个坑，时刻需要注意如果父元素存在左子节点，不一定存在右子节点，因此还需要对右子节点的下标是否超过数据个数作判定。
? ? ? ? 下滤函数完成后，删除数据自然信手拈来：
//删除数据
void HeapPop(Heap** ptr_heap)
{
//堆地址有效性检查
if (!ptr_heap || !*ptr_heap)
{
fprintf(stderr, "Heap Address NULL\n");
return;
}
//空堆直接返回
if ((*ptr_heap)->size == 0)
{
fprintf(stderr, "Empty Heap\n");
return;
}
(*ptr_heap)->data[0] = (*ptr_heap)->data[(*ptr_heap)->size - 1];
(*ptr_heap)->size--;
//空间过剩则回收
if ((*ptr_heap)->size < (*ptr_heap)->capacity / 2 && (*ptr_heap)->capacity > 4)
{
Heap* tempHeap = NULL;
while (!tempHeap)
{
tempHeap = (Heap*)realloc(*ptr_heap, sizeof(Heap) + sizeof(DATATYPE) * (*ptr_heap)->capacity / 2);
}
*ptr_heap = tempHeap;
(*ptr_heap)->capacity /= 2;
}
//下滤
HeapFilterDown(*ptr_heap);
}? ? ? ? 这里还多加了回收多余空间的语句，这步可以省略。因为堆的使用往往是一次性的，它不是用来长久保存数据的，更像是辅助其他算法的一种临时结构，所以用过之后即销毁，就没必要中途回收空间了。
3.3、其他功能
? ? ? ? 这部分功能可有可无这里仅展示代码，当然也可以根据自己需要另外添加其他功能。
//获取堆顶数据
DATATYPE HeapGetData(Heap* heap)
{
//堆地址有效性检查
if (!heap)
{
fprintf(stderr, "Heap Address NULL\n");
return -1;
}
//空堆直接返回
if (heap->size == 0)
{
fprintf(stderr, "Empty Heap\n");
return -2;
}
return heap->data[0];
}
//打印堆顶数据
void HeapPrint(Heap* heap)
{
//堆地址有效性检查
if (!heap)
{
fprintf(stderr, "Heap Address NULL\n");
return;
}
//空堆直接返回
if (heap->size == 0)
{
fprintf(stderr, "Empty Heap\n");
return;
}
printf(DATAPRT" ", heap->data[0]);
}
//打印堆
void HeapPrintAll(Heap* heap)
{
//堆地址有效性检查
if (!heap)
{
fprintf(stderr, "Heap Address NULL\n");
return;
}
//空堆直接返回
if (heap->size == 0)
{
fprintf(stderr, "Empty Heap\n");
return;
}
int enterSite = 0;
for (int i = 0; i < heap->size; i++)
{
printf(DATAPRT" ", heap->data[i]);
if (enterSite == i)
{
printf("\n");
enterSite = enterSite * 2 + 2;
}
}
}? ? ? ? 最后别忘了在 heap.h 中加入声明：
//获取堆顶数据
extern DATATYPE HeapGetData(Heap*);
//打印堆顶数据
extern void HeapPrint(Heap*);
//打印堆
extern void HeapPrintAll(Heap*);4、堆排序
4.1、测试
? ? ? ? 堆最常见的作用便是堆排序了。因为堆的特性是根节点的数据是整个堆的最大值或者最小值，而且下滤的效率比很多排序方法都高。刚好上面完成的堆结构还没进行测试，所以这里以堆排序作测试。
? ? ? ? main.c 中 main 函数补充如下：
int main()
{
//堆排序测试
DATATYPE src[30] = { 25,73,60,108,104,336,457,90,668,732,102,1,752,262,776,538,410,442,962,228,873,656,260,18,24,733,520,1414,339,439 };
DATATYPE dest[30] = { 0 };
//建堆
Heap* heap = HeapCreate();
//将src中的元素入堆
for (int i = 0; i < 30; i++)
{
HeapPush(&heap, src[i]);
}
//堆排序
for (int i = 0; i < 30; i++)
{
dest[i] = HeapGetData(heap);
HeapPop(&heap);
}
//输出排序前后结果
printf("\n排序前： ");
for (int i = 0; i < 30; i++)
{
printf("%d ", src[i]);
}
printf("\n排序后： ");
for (int i = 0; i < 30; i++)
{
printf("%d ", dest[i]);
}
//销毁堆
HeapDestroy(&heap);
return 0;
}? ? ? ? 调试得到结果：
? ? ? ? 就此测试完成。
4.2、优化思路
? ? ? ? 实际上堆排序上述方式有点拖沓了。由于堆往往用后即毁，所以在进入排序步骤时，不再另外创建数组，二十直接在堆中操作。此时堆的结构虽然被破坏了，但都到这一步了，基本面临销毁，在销毁前加以利用还能节省空间。
? ? ? ? 上述思路的堆排序与删除数据仅有一点点区别，在于，排序时，是将根节点与最末尾节点进行互换，而非覆盖。流程如下图：
? ? ? ? ?因此，只需要把删除数据的函数改改：
//堆排序
void HeapSort(Heap* heap)
{
//堆地址有效性检查
if (!heap)
{
fprintf(stderr, "Heap Address NULL\n");
return;
}
//空堆直接返回
if (heap->size == 0)
{
fprintf(stderr, "Empty Heap\n");
return;
}
//排序
while (heap->size)
{
//交换头尾数据
DATATYPE temp = heap->data[0];
heap->data[0] = heap->data[heap->size - 1];
heap->data[heap->size - 1] = temp;
heap->size--;
//下滤
HeapFilterDown(heap);
}
}? ? ? ? 别忘了在 heap.h 中声明：
//堆排序
extern void HeapSort(Heap*);? ? ? ? 之后重写?main 函数：
int main()
{
//堆排序测试
DATATYPE src[30] = { 25,73,60,108,104,336,457,90,668,732,102,1,752,262,776,538,410,442,962,228,873,656,260,18,24,733,520,1414,339,439 };
//建堆
Heap* heap = HeapCreate();
//将src中的元素入堆
for (int i = 0; i < 30; i++)
{
HeapPush(&heap, src[i]);
}
//堆排序
HeapSort(heap);
//重新指定下size，不然打印不出来
heap->size = 30;
//打印
HeapPrintAll(heap);
//销毁堆
HeapDestroy(&heap);
return 0;
}? ? ? ? F5 走起：
? ? ? ? 结果正确。完事！
4.3、衍生 TopK 算法
? ? ? ? 堆除了排序之外，还可用于解决 TopK 问题。首先，什么是 TopK ？
? ? ? ? 一句话解释， TopK 就是取数据列表中最大或者最小的前 K 个数据。回想堆排序的过程，HeapSort 函数中的 while 循环 n 次是排序 n+1 个数据列表中的最值，那么，是否可以理解成堆排序实际上就是 K 等于数据个数 -1 的?TopK 算法？
? ? ? ? 换个方式说，堆排序是对所有节点进行排序，而 TopK 只需排序前 K 个节点即可，也就是说，假设数据个数是 n ，堆排序是对堆进行 n-1 次首尾互换后下滤操作，而 TopK 则是执行 K-1 次首位互换后下滤的操作。其中，K ≤ n 。
? ? ? ? 改改 HeapSort 函数就行了，所以这里补贴代码了，各位可以自行尝试。本篇至此结束。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 单链表（C/C++）
- 2023 你会不会一直在，就像我从未离开
- 见鬼了，百度接口查询行政区划查出3个澳门了！！！
- 机器学习没那么难，Azure AutoML帮你简单3步实现自动化模型训练
- 哪个云服务器便宜又好？腾讯云新人特价云服务器，可选优惠多年
- 3.三极管和MOS管
- 算法设计与分析 | 一般背包问题
- 【已解决】RAR压缩文件可以转换为ZIP格式吗？
- android中.9图如何制作
- 【深蓝学院】移动机器人运动规划--第1章 运动规划介绍与地图构建--笔记