LeetCode 42 接雨水

题目描述

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

提示：

• n == height.length
• 1 <= n <= 2 * 104
• 0 <= height[i] <= 105

解法

解法1：动态规划

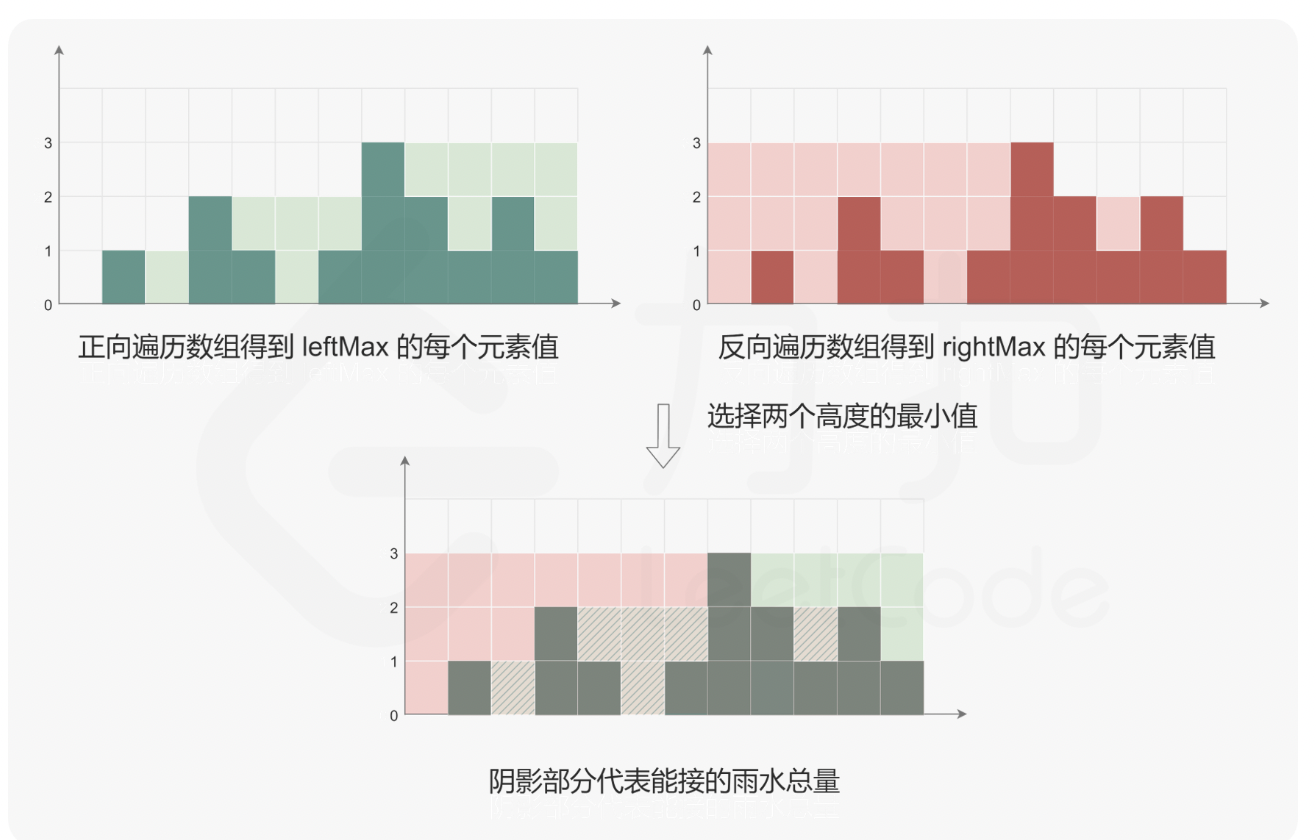
对于下标 i，下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值。

下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。

使用动态规划找到下标 i 两边的最大高度。

java代码：

class Solution {
    public int trap(int[] height) {
    int n = height.length;
        if (n <= 2) {
            return 0;
        }

        // 先找左边的最大值
        int[] leftMax = new int[n];
        leftMax[0] = height[0];
        for (int i = 1; i < n; ++i) {
            leftMax[i] = Math.max(leftMax[i-1], height[i]);
        }

        // 再找右边的最大值
        int[] rightMax = new int[n];
        rightMax[n-1] = height[n-1];
        for (int i = n -2; i >= 0; --i) {
            rightMax[i] = Math.max(height[i], rightMax[i + 1]);
        }

        // 计算每个单元能存储的水量
        int res = 0;
        for (int i = 0; i < n; ++i) {
            res += Math.min(leftMax[i], rightMax[i]) - height[i];
        }
        return res;
    }
}

复杂度

• 时间复杂度：O(n)，其中 n 为数组的长度
• 空间复杂度：O(n)。

解法2：双指针

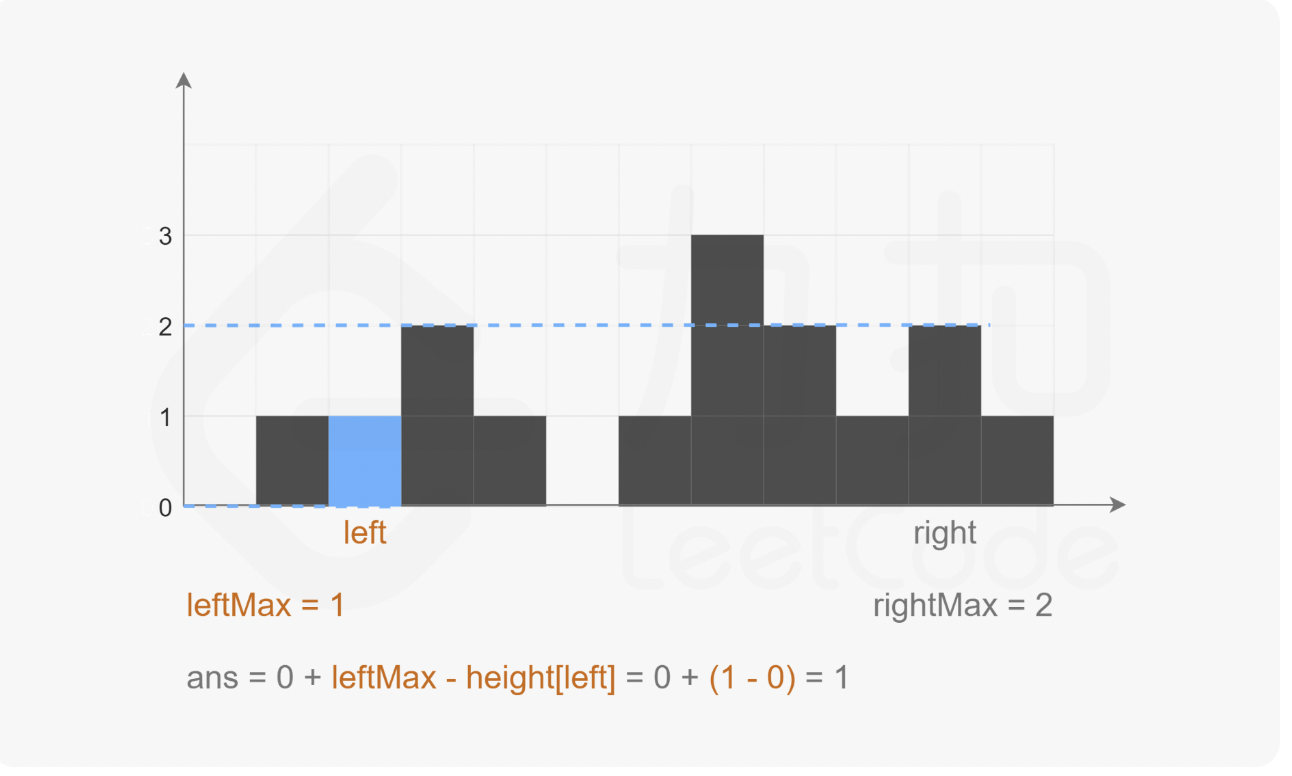
分别使用leftMax左指针表示从左边遍历，目前为止的最大值，rightMax右指针表示从右边遍历，目前为止的最大值。

如果 leftMax < rightMax，那么左边遍历到的当前柱子，左边的最大值可以确认了，但是它的右边最大值还没有遍历完，无法确认。但是我们再想想，右边虽然还不知道最大值，但是我们知道了右边当前的最大值，所以可以说，左边遍历到的当前柱子，右边的最大值最小也是rightMax。又由于leftMax < rightMax，当前柱子盛的水是由左右两边最大值的最小值决定的，所以我们已经可以计算出当前柱子的盛水量了，即：

当前柱子的盛水量 = min(leftMax , rightMax) - 当前柱子高度

同理leftMax > rightMax。

java代码：

class Solution {
    public int trap(int[] height) {
        int left = 0;
        int right = height.length -1;
        int leftMax = 0;
        int rightMax = 0;
        int res = 0;

        while (left < right) {
            leftMax = Math.max(leftMax, height[left]);
            rightMax = Math.max(rightMax, height[right]);
            if (leftMax < rightMax) {
                res += leftMax - height[left];
                left ++;
            } else {
                res += rightMax - height[right];
                right --;
            }
        }
        return res;
    }
}

复杂度

• 时间复杂度：O(n)，两个指针的移动总次数不超过 n。
• 空间复杂度：O(1)。

解法3：单调栈

什么是单调栈：栈内的元素是单调的，依次将元素压入栈，如果当前元素小于等于栈顶元素则入栈，如果大于栈顶元素则先将栈顶不断出栈，直到当前元素小于或等于栈顶元素为止，然后再将当前元素入栈。

思路：

依次从左到右遍历柱子高度

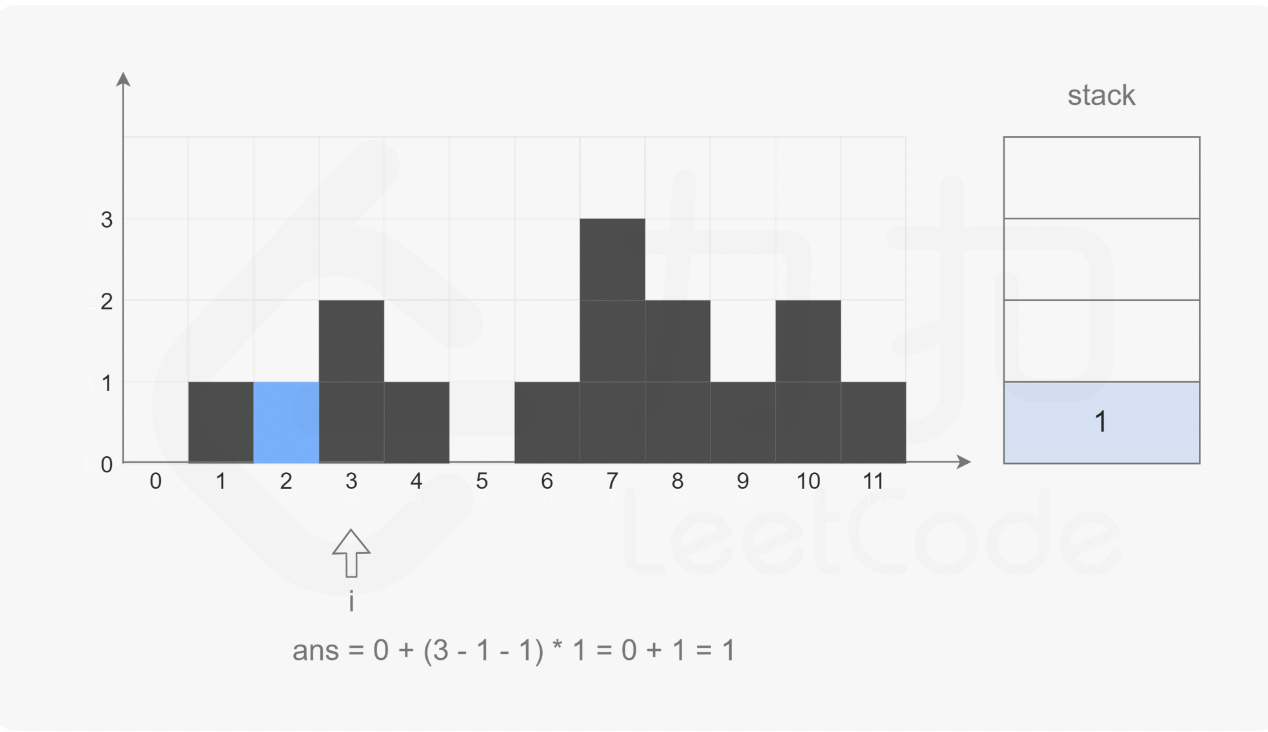
• 如果当前柱子高度比前一个小，或栈是空的，则当前数字的下标入栈
• 如果当前柱子高度比前一个大，说明前一个柱子的两边都比它高，形成了"洼地"，可以接到雨水了。此时，计算栈顶元素水的高度，弹出栈，继续向前找是否还有比当前柱子小的，依次计算，知道栈为空或者在栈里找到比当前柱子大伙相等的

java代码：

class Solution {
    public int trap(int[] height) {
        int left = 0;
        int right = height.length -1;
        int leftMax = 0;
        int rightMax = 0;
        int res = 0;

        while (left < right) {
            leftMax = Math.max(leftMax, height[left]);
            rightMax = Math.max(rightMax, height[right]);
            if (leftMax < rightMax) {
                res += leftMax - height[left];
                left ++;
            } else {
                res += rightMax - height[right];
                right --;
            }
        }
        return res;
    }
}

复杂度

• 时间复杂度：O(n)，两个指针的移动总次数不超过 n。
• 空间复杂度：O(n)。