线性回归应用梯度下降法

应用梯度下降法解决线性回归问题

梯度下降法的原理

梯度下降法原理小结-CSDN博客

由于时间原因没有仔细的讲解代码的每一步,但只要明白梯度下降法的原理和熟悉python语法应该可以看懂.

前言

一、建立数据

二、使用梯度下降法

1.定义获取损失函数

2.计算梯度信息并更替

3.运行函数

总结

---

前言

实例需要一定的理论基础,不懂梯度下降法的可以看我上面给的链接,这部分实例会让你更加理解梯度下降法在深度学习中的作用.

---

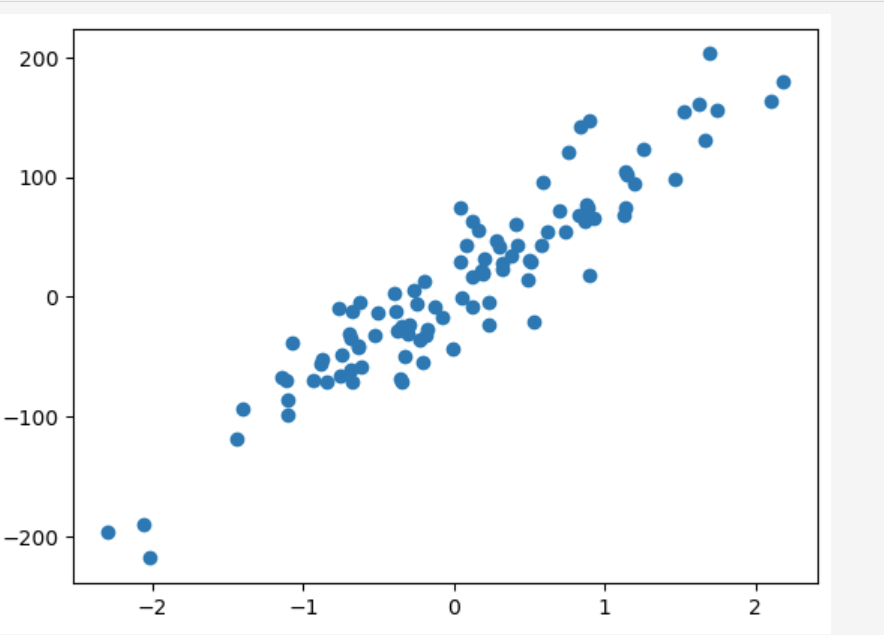
一、建立数据

应用sklearn中的make_regression创建带噪声的回归数据样本

from sklearn.datasets import make_regression
X,Y=make_regression(n_samples=100, n_features=1,n_targets=1,noise=30,random_state=1)
Y = Y.reshape(len(X),-1)

将数据组合成点

画出散点图

plt.scatter(points[:,0],points[:,1])
plt.show()

二、使用梯度下降法

1.定义获取损失函数

def compute_error_line_given_points(b , w, points):
    total_Error = 0
    for i in range(0,len(points)):
        x = points[i,0]
        y = points[i,1]
        total_Error += (y-(w * x + b))**2
    return total_Error

2.计算梯度信息并更替

这部分就是梯度下降法参数的更新算法

def step_gradient(b_current, w_current,points,learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0,len(points)):
        x = points[i,0]
        y = points[i,1]
        b_gradient += -(2/N) * (y - (w_current * x + b_current))
        w_gradient += -(2/N) * (y - (w_current * x + b_current)) * x
    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b,new_w]

3.运行函数

主要的目的是显示出所求的参数最优解,和每次损失函数的学习曲线

def run(points):
    learningRate = 0.01
    initial_b = 0
    initial_w = 0
    num_iteration = 1000
    list1 = []
    print("开始梯度下降:b的初值为{0},w的初值为{1},学习率为{2},迭代次数:{3}次".format(initial_b,initial_w,learningRate,num_iteration))
    print("Running")
    obj = gradient_descent_runner(points,initial_b,initial_w,learningRate,num_iteration)
    b = obj[0][0]
    w = obj[0][1]
    list1 = obj[1]
    print("结束梯度下降:b = {0},w = {1},error = {2}".format(b,w,compute_error_line_given_points(b,w,points)))
    plt.scatter(points[:,0],points[:,1])
    x = np.linspace(-3, 3, 50)
    y = w*x + b
    plt.plot(x, y)
    plt.show()
    return list1

函数返回的list1就是损失函数的变化值

调用run函数,将数据传进去

list1 = run(points)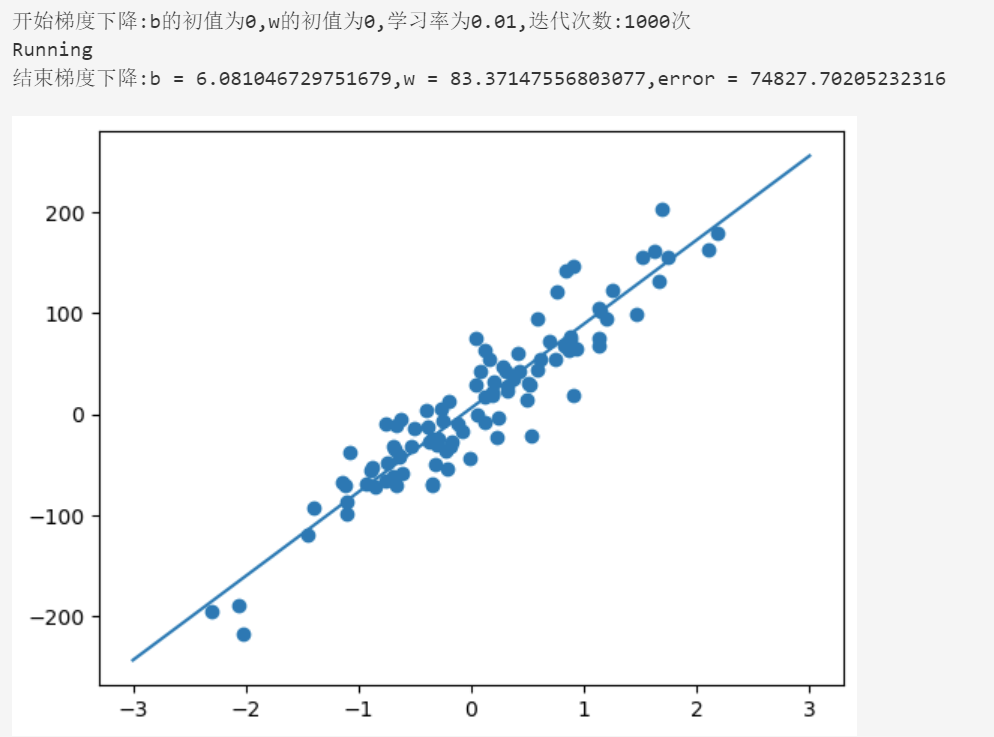

损失函数的学习曲线

plt.plot(range(1,len(list1)+1),list1)
plt.show()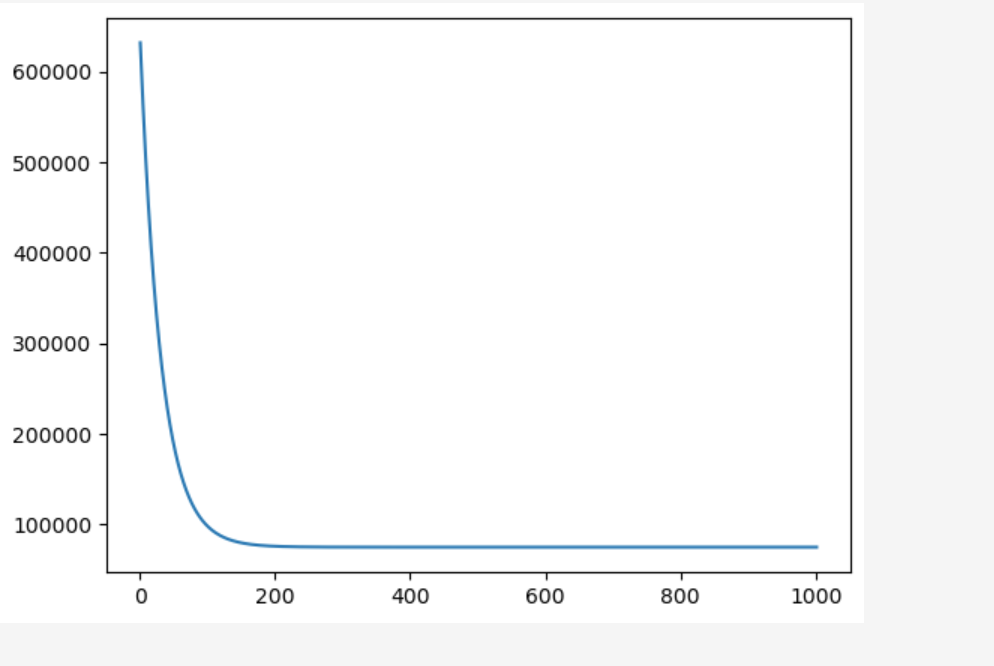

---

总结

本文章使用梯度下降算法对线性回归问题进行求解,主要部分就是梯度下降法的算法实现思想,其实还是蛮简单的,但要注意学习率learningRate和迭代次数本人刚开始将迭代次数设小了,导致没有效果,一定要注意这两个超参数.