应用回归分析(6):多重共线性
6.1 违背的原则

注意:完全多重共线性;复共线性
6.2 出现的情形
完全不想关的变量很少见,当他们之间的相关性较弱时就可以看作是复合多元线性回归矩阵的设计要求。
1、经济问题涉及时间序列
2、截面数据建立的回归方程(截面数据(cross-section data)是指在同一时间(时期或时点)截面上反映一个总体的一批(或全部)个体的同一特征变量的观测值 [1] ,是样本数据中的常见类型之一。例如,工业普查数据,人口普查数据,家庭收入调查数据。)
3、采集的样本量小于自变量的个数也会导致多重共线性(罕见病的研究)
4、模型中引入滞后变量也是可能造成多重共线性
6.3 多重共线性对回归模型的影响
一般是存在近似多重共线性!完全多重共线性比较少见!、
总结在这里,下方有证明!

6.3.1 回归系数的方差变大
(1)理论部分


这样,虽然可以得到的 无偏估计,但是估计值
的方差很大,不能正确判断解释变量对被解释变量的影响程度,甚至导致估计量的经济意义无法解释。
(2)举例部分
以二元回归方程为例子:
2.4_二元线性回归模型及参数估计 - 百度文库 (baidu.com)



6.3.2 回归系数置信区间变宽
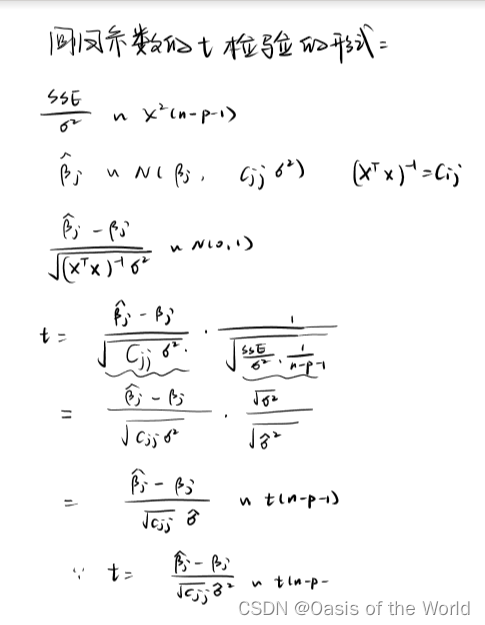

因为变大,所以置信区间也变大了。
6.3.3 T检验值较小,回归系数不显著

下边的那个统计量写错了。

6.3.4 出现决定系数较大,但是t值都不显著的情况,得出错误结论
原因:多重共线性相当于多了自变量,自变量增多会导致残差平方和变小,进而导致决定系数变大。因此可能会出现决定系数较大的情况
6.3.5 OLS估计值及其标准差对数据的微小变动很敏感,结果不稳定
OLS最小二乘法!
多重共线性导致参数的方差变得很大,数据稍微变动可能会对系数造成较大的影响
6.3.6 回归系数的符号有误,使回归方程无法得到合理的经济解释,直接影响应用效果,降低应用价值
符号可能产生逆转!
6.4 多重共线性的诊断
6.4.1 相关系数法

6.4.2 方差扩大因子法
问一下老师吧??????为什么除的那一步呢!????
(1)理论构建
【1】方差扩大因子



可以参考上方6.3.1 (2)的二元回归的形式!
【2】容忍度
小于容忍度时直接拒绝该变量加入方程哦!!!

(2)案例分析
当分析的是二元回归的情况时:

6.4.3 特征根判别法
对矩阵求特征根,如果存在多重共线性,一定会有0特征根,有多少个零特征根就有多少个多重线性关系。
【1】特征根近似为0的判断标准
用条件数


最大的特征根,比待测特征根大很多倍时说明待测特征值太小了!!!
6.4.4 直观判定法

回归方程不正常!@!
6.5 消除多重共线性的方法
6.5.1 剔除一些不重要的变量
通过逐步回归法,在上一节中有介绍到!
6.5.2 增大样本量

6.5.3 用有偏估计的一些方法
比如岭回归!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 关于Windows 10的操作中心 ,看这篇文章就可以了
- 广州大彩串口屏新品发布:大彩医用级4.3寸串口屏带U盘接口版发布
- 软件测试/测试开发/测试管理丨Page Object模式:为什么它是Web自动化测试的必备工具
- Redis的key过期策略是怎么实现的
- el-table右固定最后一列显示不全或者是倒数第二列无边框线
- Git 基本命令与操作流
- 开源数据可视化分析工具DataEase本地部署并实现远程访问
- nginx配置 请求静态文件时带上额外的响应头信息
- C++ 实现十大排序算法
- Fastboot指令大全