玩具蛇（dfs深搜）

题目

小蓝有一条玩具蛇，一共有?16?节，上面标着数字?1至?16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成?90?度角。

小蓝还有一个?4×4的方格盒子，用于存放玩具蛇，盒子的方格上依次标着字母?A?到?P?共?16个字母。

小蓝可以折叠自己的玩具蛇放到盒子里面。他发现，有很多种方案可以将玩具蛇放进去。

下图给出了两种方案：

请帮小蓝计算一下，总共有多少种不同的方案。如果两个方案中，存在玩具蛇的某一节放在了盒子的不同格子里，则认为是不同的方案。

运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

题目思路

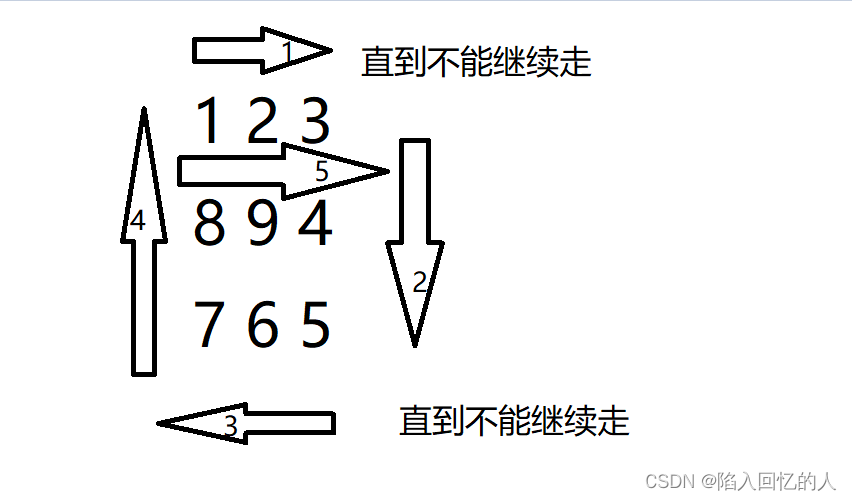
? ? ? ? 根据题目思路，我们可以看出这道题目其实就是在数组中数字，不过它要满足一种规律（只能旋转90°）；将每一种方案加起来便可以得到最终答案，利用dfs的特性（找到一种方案），不断枚举第一个节点（即从哪里开始），将这些方案加在一起，便可以得到最终答案。

源代码

java代码

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
    //定义方向：向右->向下->向左->向上
    private static final int[] dx={0,1,0,-1};
    private static final int[] dy={1,0,-1,0};
    private static int[][] g=new int[4][4];
    private static int ans=0;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...

        //遍历每个开始的位置
        for(int i=0;i<4;i++)
          for(int j=0;j<4;j++)
            {
              ans+=dfs(i,j,1);
              //记得要还原现场
              g[i][j]=0;
            }

        System.out.println(ans);
        scan.close();
    }

    private static int dfs(int x,int y,int k){
      g[x][y]=k;
      if(k==16) return 1;

      int res=0;
      for(int i=0;i<4;i++){
        int tx=x+dx[i],ty=y+dy[i];

        if(tx>=0 && tx<4 && ty>=0 && ty<4 && g[tx][ty]==0){
          res+=dfs(tx,ty,k+1);
          g[tx][ty]=0;
        }
      }

      return res;

    }
}

c++代码

#include <bits/stdc++.h>

using namespace std;

int dx[]={-1,0,1,0},dy[]={0,-1,0,1}; 
int g[4][4];
int n=4;

int dfs(int x,int y,int k)
{
    g[x][y]=k;
    
    if(k==16) return 1;
    
    int res=0;
    for(int i=0;i<4;i++)
    {
        int x1,y1;
        x1=x+dx[i],y1=y+dy[i];
        if(x1>=0 && x1<n && y1>=0 && y1<n && g[x1][y1]==0)
        {
            res+=dfs(x1,y1,k+1);
            g[x1][y1]=0;
        }
    }
    
    return res;
}

int main()
{
    int res=0;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        {
            res+=dfs(i,j,1);
            g[i][j]=0;
        }
    cout << res << endl;
    return 0;
}

?