L1-071 前世档案(Java)

网络世界中时常会遇到这类滑稽的算命小程序，实现原理很简单，随便设计几个问题，根据玩家对每个问题的回答选择一条判断树中的路径（如下图所示），结论就是路径终点对应的那个结点。

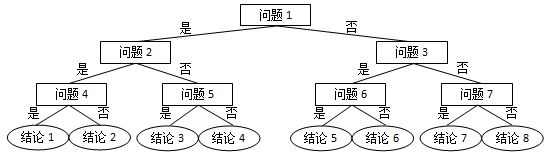
现在我们把结论从左到右顺序编号，编号从 1 开始。这里假设回答都是简单的“是”或“否”，又假设回答“是”对应向左的路径，回答“否”对应向右的路径。给定玩家的一系列回答，请你返回其得到的结论的编号。

输入格式：

输入第一行给出两个正整数：N（≤30）为玩家做一次测试要回答的问题数量；M（≤100）为玩家人数。

随后 M 行，每行顺次给出玩家的 N 个回答。这里用 y 代表“是”，用 n 代表“否”。

输出格式：

对每个玩家，在一行中输出其对应的结论的编号。

输入样例：

3 4
yny
nyy
nyn
yyn

输出样例：

3
5
6
2

解题思路

这个方法的核心思想是将玩家的答案序列直接转换为二进制数，然后将其转换为对应的十进制数。利用了二叉树的性质和二进制数的表示方式。

每个“是”（'y'）被替换为二进制的 0，每个“否”（'n'）被替换为二进制的 1。然后，这个二进制字符串被转换为十进制数。由于二进制数从 0 开始计数，而结论编号从 1 开始，所以需要在最后的结果上加 1。

解题过程中遇到的问题

原本我的思路是

1. 初始化一个变量 index 为 1，代表当前节点的编号（根节点）。
2. 对于每个玩家的答案序列，从左到右遍历。

• • 如果答案是 'y'（代表“是”），则 index 变为 index * 2（移动到左子节点）。
  • 如果答案是 'n'（代表“否”），则 index 变为 index * 2 + 1（移动到右子节点）。

1. 在遍历结束后，index 将指向叶子节点，其编号%8对应结论的索引即为玩家的结论编号。

int[] indexClusion = new int[]{1,2,3,4,5,6,7,8};

后来想了想，我的N不一定是3，也就是说所对应的结论索引可能会大于8，这也就是为什么我只过了第一个测试点，真的是愚蠢至极了......

错误代码:

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt(); // 问题数量
        int M = scanner.nextInt(); // 玩家人数
        scanner.nextLine(); // 跳过行尾

        int[] indexClusion = new int[]{1,2,3,4,5,6,7,8};

        for (int i = 0; i < M; i++) {
            String answers = scanner.nextLine();
            System.out.println(calculateConclusionIndex(answers,indexClusion));
        }
    }

    private static int calculateConclusionIndex(String answers,int[] indexClusion) {
        int index = 1;
        for (char answer : answers.toCharArray()) {
            if (answer == 'y') {
                index *= 2;
            } else {
                index = index * 2 + 1;
            }
        }
        return indexClusion[index%8] ;
    }
}

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt(); // 问题数量
        int M = scanner.nextInt(); // 玩家人数
        scanner.nextLine(); // 跳过行尾

        for (int i = 0; i < M; i++) {
            String answers = scanner.nextLine();
            System.out.println(calculateConclusionIndex(answers));
        }
    }

    private static int calculateConclusionIndex(String answers) {
        // 将答案中的'y'和'n'分别替换为二进制的'0'和'1'
        String binaryString = answers.replace("y", "0").replace("n", "1");
        // 将二进制字符串转换为十进制数，并加1以匹配结论编号的开始值
        return Integer.parseInt(binaryString, 2) + 1;
    }
}