硅像素传感器文献调研（二）

写在前面：从上篇文章的参考文献中看到一篇文献，现在也精读一下，今天还有一个任务是把上篇文献整体脉络用流程图的形式完整梳理一下。

哈哈哈哈哈哈：代表没太搞明白的部分

如何写论文：

引言部分：基础理论，点出前人的一些不足，引出自己研究内容的重要性。然后简要介绍全文的研究内容。

1991-金属场板+保护环结构

?带场板和保护环的高压平面结的二维分析和设计考虑

0.摘要

配备有场板和保护环的平面结（非穿通和穿通情况）的击穿电压是通过使用有限差分法求解二维泊松方程计算的电势分布来评估电离积分来确定的。各种参数，如衬底掺杂浓度，n层厚度，场氧化层厚度，圆柱结曲率，场板宽度，场板和保护环之间的间距，对于击穿电压的影响进行了广泛的研究。结果表明，场氧化层厚度存在一个最佳值，以实现最大的击穿电压。研究还表明，最佳的氧化层厚度取决于圆柱结曲率，衬底掺杂浓度，和n层厚度。进一步表明，当击穿发生在场板边缘时，场板结构上钝化介质层的介电常数影响击穿电压。数值计算结果与实验数据进行了比较，两者之间有很好的一致性。基于这个二维的研究，提供了设计准则，通过保存的器件面积和减少在场板边缘的电离以实现击穿电压接近最大可实现的值。本文中提出的结果清楚地表明，在实现给定的击穿电压的场板设计采用穿通结构比非穿通结构的优越性。

1.引言

场板平面结终端技术通常用于分立器件、功率MOS器件、MOS双极器件、高压IC和功率IC 的高压结的设计。该技术具有面积小、制作工艺简单等优点，是其他端接技术中的上级技术。因此，这种结构的相关的击穿电压的各种参数的完整分析对于优化目的是非常重要的。

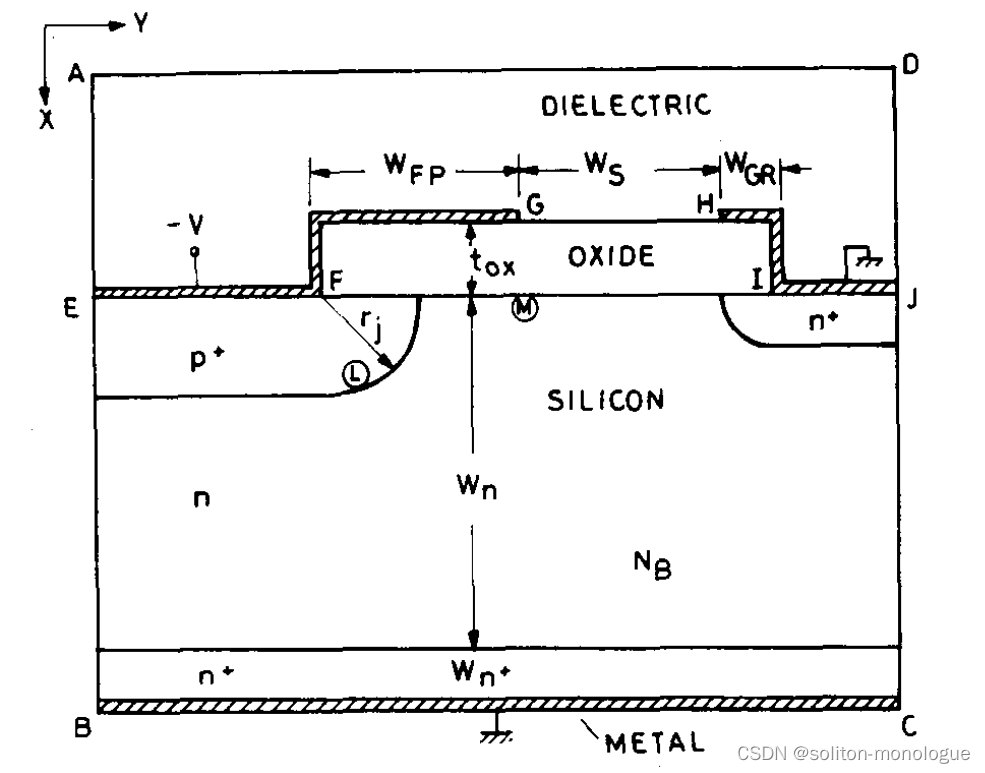
?图1 配有场板和保护环的平面结的结构。L和M表示峰值电场的位置。

?在本文中，符号BVFP，用于表示平面结的击穿电压，包括非穿通（NPT）和穿通（PT）类型，配有图1所示的场板和保护环。参考附图，确定BVFP的参数为：1）NB-衬底掺杂浓度，2）tox，场板下面的氧化物的厚度，3）rj，-圆柱形结的半径，4）WFP，场板的宽度，5）Ws，-场板和保护环之间的电极间间距的宽度，以及6）Wn，场氧化物下方的n层的厚度，其是穿通结构的附加参数。这些参数可以分为两类：衬底参数和工艺参数。衬底参数NB和Wn取决于所选择的硅衬底;这些参数的仔细和明智的选择是必要的，同时牢记所需的最大BVFP要求。可在制造期间调整工艺参数tox、rj、WFP、Ws以获得所要结果。

文献调查显示，在迄今为止报告的研究中[8]-[16]，尚未考虑所有上述参数对BVFP的影响;特别是，忽略了rj的影响。由于这一缺点，虽然已有关于tox与BVFP的一些结果[8]，[11]，[ 15]，但它们的应用受到限制。此外，Clark和Zoroglu [9]，[10]已经通过实验显示了BVFp对WFp和Ws的强烈依赖性。然而，这些参数的理论研究没有在文献中。因此，为了实现设计优化，对于给定的NB和Wn，必须很好地理解tox，rj，WFP和Ws对BVFP的影响。此外，可以注意到，迄今为止在文献中还没有研究沉积在场板结构上的钝化电介质层的相对介电常数Edie对BVFP的影响。

鉴于上述情况，本文的目的是：（1）建立具有场板和保护环的平面结的击穿电压模型，并考虑到tox，rj，WFP，和Ws，对给定的NB和Wn的影响;（2）研究Edie对BVFP的影响。开发了一个用于器件建模的二维模拟程序“雪崩击穿分析模拟工具（STAAB）”。模型化的接头包括NPT和PT类型。从一个二维的模拟研究表明，在这两种结构中，对于一个给定的衬底参数，BVFP可以通过优化tox最大化，并且最大的BVFP和最佳的tox是rj的函数。本分析进一步表明，只有当宽度WFp和氧化物厚度tox大于其相应的最小限度时，才能实现场板的有益效果。钝化介质的Edie在确定BVFP值中扮演着重要的角色。通过与足够的实验结果的比较支持理论分析。还提供了实现击穿电压接近最大可实现值的设计准则。

2.器件几何形状和数值方法

本工作中分析的器件结构如图1所示。p+区和n+接触扩散的掺杂分布被假定为高斯分布，表面掺杂浓度No = 1019 cm-3。假设p+-n结在其终端处是圆柱形的，曲率半径r等于结深度。假设P+窗口宽度和N+保护环接触开口很大，使得不存在我们先前的论文[17]中讨论的横向曲率效应。氧化物-硅和氧化物电介质界面被假定为理想的和无电荷的。

在NPT型的平面结的分析中，n层厚度Wn被取为足够大以防止击穿时耗尽层宽度到达n +接触。对于PT情况，Wn主要决定p+-n-n+平面平行结的击穿电压BVpt。如果耗尽层到达n+接触的电压Vp与BVpt相比较小，则NB对击穿电压结果的影响可以忽略不计[18].

为了便于分析，本研究分为三组基于器件的几何形状的考虑。在第一组中，主要关注的是研究tox和rj对BVFP的影响。为了方便，场板和保护环距离Ws被认为是大的，使得BVFP不受Ws的影响。此外，场板宽度WFP也被取为大的，使得结曲率与场板边缘之间的相互作用可以忽略。

第二组研究集中于对于不同的tox值，WFp对BVFp的影响。在这里，Ws被认为是大的。

第三组的目的是研究当WFp较大时，场板和保护环间距Ws对BVFp的影响。在所有三组中，对NPT和PT情况都进行了分析。

在所研究的上述器件结构中，通过求解二维泊松方程来计算电压和电场分布。

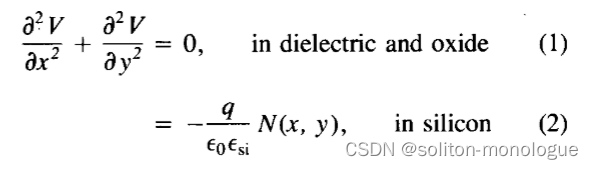
其中V（x，y）、N（x，y）分别是在点（x，y）处的电压和掺杂浓度; q是电荷，E0是自由空间的介电常数，并且Esi是硅的相对介电常数。电压的边界条件为

?方程（1）和（2），以及与文献[ 191]中描述的界面处的适当边界条件，通过有限差分法[19]-[21]求解。耗尽层逻辑[22]用于找出硅中的中性区域。

对于所研究的器件结构，上述数值场计算揭示了电场峰值出现在两个区域，即，1)在p+区内的结的弯曲部分附近，以及2）在Si-SiO2界面上的场板边缘附近（图1中的L和M）。如[22]中所述，追踪通过电场中这两个峰中的每一个的临界电离路径。接下来，对于所施加的电压VA，使用下式数值计算沿着临界路径的电离积分I的值：

基于我们最近的研究[23]，在本工作中选择由Overstraeten和DeMan [24]给出的电离系数an和ap。在计算中改变VA，使得沿着两个临界路径中的至少一个沿着计算的积分I的最大值接近1。在这种条件下施加的电压是击穿电压BVFp，对于给定的NB、Wn、rj、tox、WFP和WS，其由场板边缘和/或结边缘处的雪崩倍增控制。

3.计算结果

基于图1所示的几何模型和第2节中的讨论和方法，进行了计算，以研究各种参数对BVFP的影响。由于我们想要针对给定的一组衬底参数设计最佳可能的场板终端，因此对于NPT情况，通常在NB = 1014 cm-3处进行计算;对于PT情况，通常在NB = 1013?cm-3，Wn=100um处进行计算。击穿电压结果的归一化表示被证明是非常紧凑的，适用于广泛的参数值，最重要的是，独立于击穿电压计算中使用的电离系数[23]。在目前的工作中，耗尽层宽度Wpp在一个突然的平面平行p+-n结的击穿，和n层厚度W，被分别用作距离归一化参数NPT和PT的情况下。对于NPT的情况，对于1013 s NB 5 101 5 cmP 3，突变平面平行p+-n结的击穿电压（伏特）和相应的耗尽层宽度（cm）经验地与衬底掺杂浓度NB相关，

这些公式是在使用[24]的电离系数生成的数据的帮助下获得的，并且也适用于根据归一化击穿电压[ 171，[23]的知识来估计平面p+-n结的击穿电压，只要p+区域上的电压降可以忽略不计。

A?结曲率rj、氧化层厚度tox对击穿电压BVFP的影响

计算了带有场板和保护环的NPT和PT结的击穿电压，得到了BVFP与NB、Wn、tox和rj的关系曲线。在这组研究中，WFp和Ws被认为是大的。计算结果见图2和图3。在所有这些情况下，可以看出，BVFP经过对应于某个最佳氧化物厚度tox(opt)的最大值。根据衬底参数NB或Wn以及结深rj，tox（opt）取不同的值。对于NPT和PT情况，对于不同的运行参数值NB和Wn，BVFP相对于tox的变化趋势是相似的（图2）。然而，BVFP与tox的特性曲线（以rj为运行参数）在NPT和PT情况下是不同的（图3）。例如，对于NPT情况，对于给定rj可以实现的最大BVFP，BVFP通常随着rj的增加而增加。然而，对于PT情况，这种增加限于rj的某个最佳值，并且对于给定的n层厚度Wn，对于rJj> rj（opt），最大BVFP下降

图2?计算出的击穿电压与氧化物厚度的关系，其中背景掺杂浓度作为非穿通（NPT）情况下的运行参数，并且n层厚度作为穿通（PT）情况下的运行参数（Wpp= 135 um）。

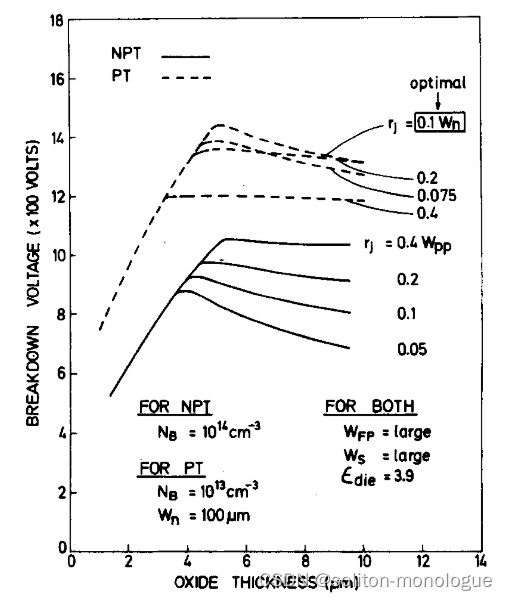
图3?计算的击穿电压与氧化层厚度的关系（圆柱形结曲率半径作为运行参数，PT和NPT的情况下（W/，/，= 135 pm）。

对击穿时沿电离临界路径的电离积分值沿着的检验表明，对于tox< tox（opt），由于M区的倍增而发生击穿（图1）。该边缘击穿电压的大小取决于衬底参数（对于NPT情况为NB，对于PT情况为Wn）和tox，但独立于rj(见图3)。对于tox>tox(opt)，倍增发生在L区(图1)，继续增加tox，BVFP逐渐下降。在这种情况下，rj在决定BVFP方面起着重要作用。在tox=tox(opt)沿两条临界路径的积分i的值是相等的；然而，L和M(见图1)处的峰值电场的大小不同。观察到M处的峰值电场远大于L处的峰值电场，且M区的电场变化幅度大于L区。

对于NPT情况，当rj较高时，BVFP的下降速率随着tox增加到而减小。此外，可以从图2和3中看出，为实现最大BVFP所需的tox(opt)除NB外还取决于rj。在PT的情况下，参考图3，对于给定的n层厚度Wn，可以看出，tox和rj都应该优化以实现最高的BVFP。此外，对于rj< rj（opt），由于结曲率效应，最大BVFP随着rj的增加而增加，并且与NPT情况下观察到的情况相似;对于rJj> rj（opt），由于结下方的n层厚度减小，BVFP减小。与NPT情况不同，PT情况下的tox（opt）不随rj的增加而增加。相反，它遵循最大BVFP的变化，在rj（opt）处达到最高值，并且在rj> rj（opt）之后下降。

图2示出了对于PT情况实现给定击穿电压所需的场氧化物厚度小于对于NPT情况。因此，在薄氧化物高压结的制造中，使用PT结构的场板设计在技术上非常有吸引力。

B 场板宽度WFp对击穿电压BVFp的影响

从有效利用硅面积的角度和从宽度WFP改善BVFP的有效性的角度来看，适当的场板宽度WFP是至关重要的。因此，一些研究人员[9]、[10]、[12]对BVFP对于WFP的依赖进行了实验研究，这些研究表明，BVFP随着WFP的增加而增加。在本二维(2D)模拟中，研究了WFP和tox对BVFP的组合效应，并且对于PT和NPT两种情况的结果如图4和图5所示。这些数字显示了文献中没有报道的几个附加特征。例如，对图4和图5的检查清楚地展示了以下内容：

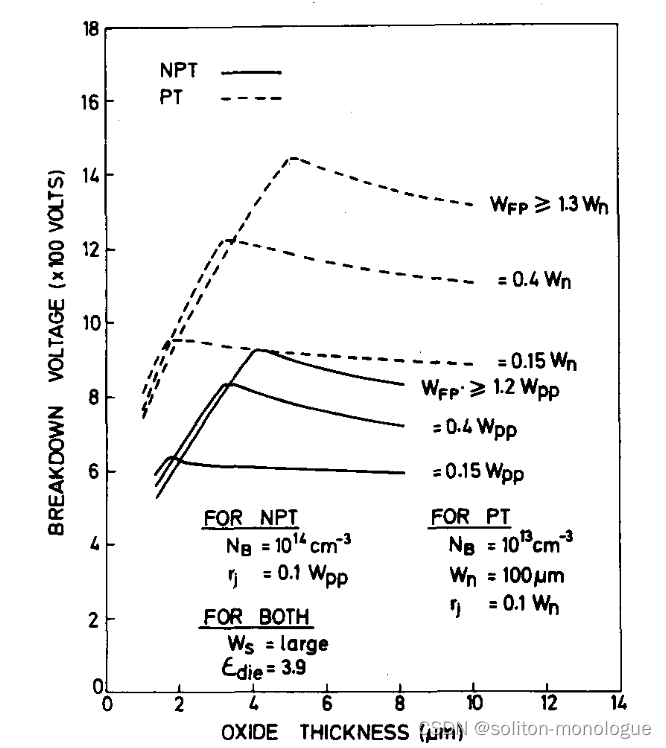
图4?计算的击穿电压与氧化层厚度的关系（场板宽度作为运行参数，PT和NPT的情况下（Wpp= 135 um）。

图5?计算的击穿电压与归一化场板宽度的关系（氧化物厚度作为运行参数），PT和NPT的情况下。对于NPT情况，WFP相对于Wpp归一化，对于PT情况，Wn相对于Wpp归一化（Wpp?= 135 pm）。

1)对于任何氧化物厚度tox≥tox(opt)，NPT情况下，随着WFP从0增加到等于1.2Wpp情况下，BVFP从BVcy增加；对于PT是到1.3Wn; 之后WFp的进一步增加不会改善BVFP。如前所述，对于tox≥?tox(opt)的这种情况，BVFP由结边缘附近的电离控制。因此，随着WFp增加，BVFp的改善是由于结边缘附近的等势线变平。一旦等势线被展开到最大可能的程度，就接近BVFP的极限值。

2）BVFP到达最大值时氧化物厚度的大小也取决于WFP的值（图4）

3）如果tox相当小，则WFp的增加不利地影响BVFP。另一方面，对于中等厚度的氧化物，BVFP经历最大值，然后随WFP进一步增加下降（图5）。对于这些情况，BVFP主要由硅中场板边缘处的倍增决定。当tox相当小时，BVFP随WFP的改善从大值减小是由于结接近而在场板边缘处的场拥挤减小的结果;当WFp趋于零时，B VFp接近B Vcy。

上述观察结果强调，在场板结终端的设计中，需要采用氧化层厚度为tox≥tox(opt)。

对图5中的曲线的斜率（在WFp小的部分中）的检查揭示，当tox小时，BVFP相对于WFp的上升速率较大。对于相当的氧化物厚度，PT情况下的ΔBVFp/ΔWFp高于NPT情况下的ΔBVFp/ΔWFp。例如，对于NPT和PT情况，针对WFp < 30 μm在tox(opt）处具体计算的ΔBVFp/ΔWFp分别为7.6和14.2V/um，这表明PT结构导致硅面积的更好利用。

C?场板和保护环间距Ws对击穿电压BVFP的影响

较大的Ws值导致硅面积的浪费。另一方面，当Ws较小时，其可通过限制等势轮廓的扩展而不利地影响BVFP，且由此增加给定电压的峰值电场。为了找到不降低BVFP的最小值Ws，对Ws的各种值进行计算，并在图6中以tox作为运行参数进行绘制。在这项研究中，WFp被认为是大的。对于给定的一组参数，增加间距Ws将BVFP增加到由衬底和其他参数确定的特定值。

图6?计算的击穿电压与场板和保护环之间的归一化间距的关系，对于PT和NPT情况。对于NPT情况，Ws相对于Wpp归一化，对于PT情况，Wn相对于Wpp归一化（Wpp= 135 μ m）。

从图6中可以看出，在PT二极管的情况下，Ws对BVFP的作用更为重要。对于氧化物厚度高于tox（opt）（对于NPT情况=4.05 μ m，对于PT情况= 5.0 μ m）的情况，击穿路径位于结附近，因此BVFp受场板边缘处发生的事件的影响相对较小。因此，可以使用更小的Ws值。因此，氧化物厚度高于tox（opt）的场板结构具有以BVFP中增加的tox和相关联的牺牲为代价来节省硅面积的能力。参考图6，对于PT情况，由于增加到tox(opt)以上而导致的BVFp的6.3%牺牲可以提供W1宽度的58%节省。

D 介电常数Edie对击穿电压BVFP的影响

在文献[25]中报道的涉及场板结构的高压器件的2D计算机模拟研究中，[26]电介质总是被认为是空气。然而，在实践中，配备有场板保护环的高压设备应该由合适的钝化剂保护，以防止表面电弧[8]，[12]。为了研究介质相对介电常数ε die对B VFP的影响，我们模拟了两种相同结构只有ε die不同的VFP，结果表明，当ε die = 3.9时，对应的B VFP明显高于ε die = 1.0时的VFP，从而说明ε die在决定B VFP中起着重要作用。仔细观察两种不同Edle情况下的电势和电场分布，发现当Edle较大时，等势线在靠近场板边缘的介质中展开。因此，对于给定的电压，硅中的电场减小，导致更高的B VFP。

为了证明Edie对击穿电压的影响，将通过2D模拟获得的BVFp与tox（见图7）绘制成图，Edle = 1.0、3.9和11.7分别对应于空气、SiO和硅。对于这种情况，WFp和Ws被认为是大的。可以看出，对于tox<tox（opt）发生的边缘击穿对Edle的变化非常敏感，而对于tox>tox(opt)的击穿电压实际上不受Edle的变化的影响。此外，清楚的是，如果使用较大的Edle，则可以以较小的tox实现给定的B VFP。还可以看出，如果钝化剂电介质的Edle较大，则实现最大B VFP所需的最佳氧化物厚度tox（opt）较低。

据观察，在目前的工作中，应用较大Edle的钝化层给予较高的BVFp（在给定的场板宽度WFP下）。因此，如果采用更大的Edle，则对于给定的B VFp，可以减小WFp长度，从而有效地利用可用的硅面积。

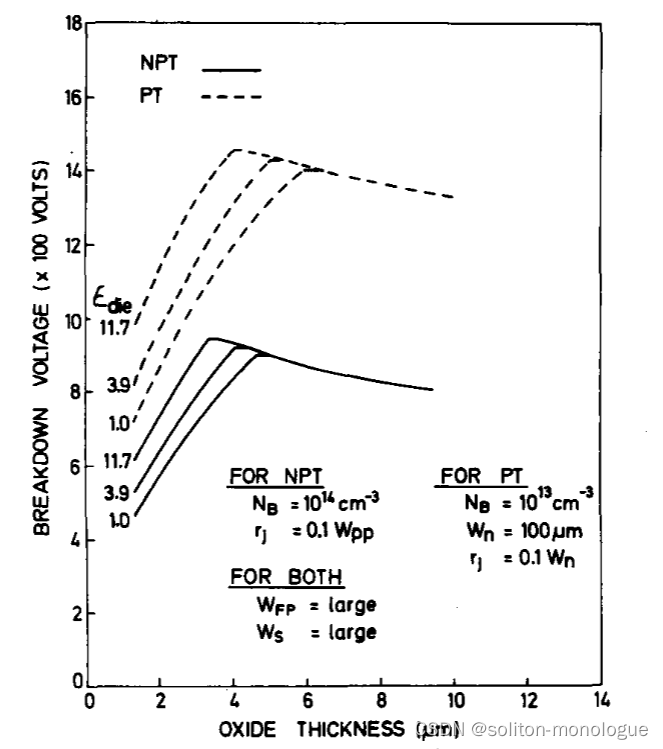
图7?计算了钝化介质的不同相对介电常数下的击穿电压与氧化层厚度的关系。对于PT和NPT两种情况（Wpp= 135 um）。

4.与实验的比较

为了验证在前一节中讨论的计算结果，并验证在这项工作中开发的计算机程序的数值精度，在我们的实验室进行实验。本模拟的结果也比较了几套文献[8]、[ 111]中关于场板二极管击穿电压的实验数据。这些结果在表1中，有关于器件结构的显著参数的信息，该器件结构的实验测量的击穿电压数据与本工作估计的值进行比较。可以看出，本模拟和实验之间有很好的一致性，从而验证了本2D建模的努力。

表1：本工作的击穿电压与之前工作8和11实验结果的比较。

还将本模拟估算的击穿电压与文献[9]中关于BVFP随WFP变化的实验数据进行了比较。对于WFP在20和50 um范围内，通过将曲线拟合到[9]的实验点和通过本模拟计算的ΔB VFp/ΔWFp分别为11.3和10.9 V/pm，从而进一步为本模拟提供实验支持。

5. 设计考虑

基于第3节中给出的分析，我们在此讨论对于给定的衬底参数NB（对于NPT情况）或Wn（对于PT情况），通过适当地调整工艺参数rj、tox、WFP、和Ws来获得接近最大可实现值的BVFP的场板设计考虑。设计标准为：1）将最大电离路径限制在结的弯曲部分;以及2）保存器件所占据的硅面积。

对于NPT的情况，沿着rj的NB确定最大BVFP，其可以在tox被优化为tox(opt)实现。在图3中，可以看出，对于r j<0.1Wpp，B VFP随tox>tox(opt)增长从其最大值大幅下降。另一方面，当rj≥?0.1 Wpp时，B VFP的下降相对较小。然而，更大的rj值需要相应更高的tox(opt)值。另外，最大BVFP的增加与rj的增加不相称，因为我们通常可以在没有场板的圆柱形结中得到。因此，选择rj?= 0.1 Wpp对于NPT结构来说是非常合适的，以获得具有较小rj的最佳结果。目前的研究表明，最佳的氧化层厚度tox(opt)可以通过经验拟合表示为

略略略。重点在看懂绘制的几幅图。

6.结论：

在本文中，平面结（NPT和PT的情况下）配备场板和保护环进行了分析，首次考虑到所有的显着参数，使用为此目的而开发的二维计算机模拟程序STAAB。系统地研究了衬底参数NB、Wn和工艺参数rj、tox、WFP和Ws对这种结击穿电压的影响。它证明了NPT和PT的情况下，最大的击穿电压发生在一组给定的衬底参数和结深度时，氧化物厚度进行优化到tox(opt)处。也证明了最佳结深度的存在（PT的情况下），这给出了对于一个给定的n层厚度最好的击穿电压。此外，对WFp和tox的组合效应的研究已经表明，只有当tox≥tox(opt)，WFP的增加才导致击穿电压的增强，并且超过WFp = 1.2Wx，（对于NPT）或1.3Wn（对于PT）时，该改进是可以忽略的。然而，tox<tox(opt)，但高于某个最小tox时，示出了BVFP相对于WFP的变化经历最大值，并且当tox低于某个临界值时，WFP的增加不利地影响BVFP。它还表明，BVFP随着Ws的增加而增加，并接近一个常数。钝化介质层的介电常数的影响进行了研究，它表明，较高的值的Edle所需的一个给定的击穿电压允许减少在tox和WFp。

计算结果与几组实验数据的比较表明，有很好的一致性，验证了目前的分析和验证的计算机程序的准确性，在这项工作中开发的计算击穿电压。基于限制的最大电离路径的结的弯曲部分，并保存设备所占用的硅面积的设计考虑，建议。

对基于PT结构和NPT结构的场板设计进行了比较性能评价，证明了PT结构优于NPT结构。结果表明，PT结构需要更少的氧化层厚度来实现给定的B VFP，并且在相当的氧化层厚度下，随着场板宽度W的增加，提供了更大的B VFP增加。它还表明，可以实现使用PT结构的BVFP是更接近相应的理想平面平行击穿电压比可以实现使用NPT结构。