E : DS查找—二叉树平衡因子

Description

二叉树用数组存储，将二叉树的结点数据依次自上而下,自左至右存储到数组中，一般二叉树与完全二叉树对比，比完全二叉树缺少的结点在数组中用0来表示。

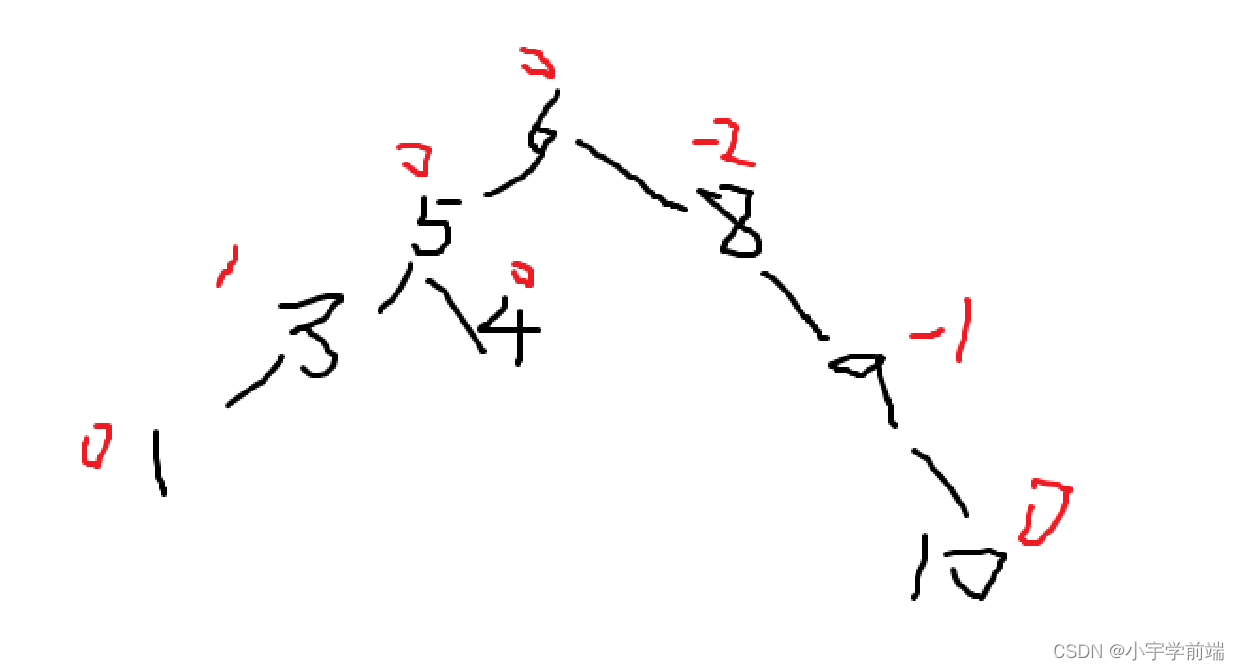
计算二叉树每个结点的平衡因子，并按后序遍历的顺序输出结点的平衡因子。

–程序要求–

若使用C++只能include一个头文件iostream；若使用C语言只能include一个头文件stdio.h
程序中若include多过一个头文件，不看代码，作0分处理
不允许使用第三方对象或函数实现本题的要求

Input

测试次数t

每组测试数据一行，数组元素个数n，后跟n个字符，二叉树的数组存储。

Output

对每组测试数据，按后序遍历的顺序输出树中结点的平衡因子（测试数据没有空树）

Sample

#0

Input

2
6 ABC00D
24 ABCD0EF0000H00000000000I

Output

B 0
D 0
C 1
A -1
D 0
B 1
I 0
H 1
E 2
F 0
C 2
A -2

#include <iostream>

using namespace std;

// 二叉树结点的定义
struct TreeNode {
    char data;
    int Height;//结点所处的高度
    int balanceFactor;//结点的平衡因子
    TreeNode* left;
    TreeNode* right;
    TreeNode():balanceFactor(0), Height(0), left(nullptr), right(nullptr) {}
    TreeNode(char value) : data(value), Height(0), balanceFactor(0), left(nullptr), right(nullptr) {}
};

// 计算平衡因子
int calculateBalanceFactor(TreeNode* node) {
    //后序遍历的原因，第一个访问的结点高度是0

    //计算左子树高度：若左子树为空，则左树高为0，否则为左树高度+1
    int leftHeight = (node->left == nullptr) ? 0 : node->left->Height + 1;
    //右树相同
    int rightHeight = (node->right == nullptr) ? 0 : node->right->Height + 1;

    //给结点的高度赋值，取左右子树中更大的那个
    if (leftHeight > rightHeight)node->Height = leftHeight;
    else node->Height = rightHeight;

    //最后返回平衡因子的大小
    return leftHeight - rightHeight;
}

// 后序遍历并计算平衡因子
void postOrderTraversal(TreeNode* node) {
    //直接先走到底层
    if (!node ) {
        return;
    }

    // 遍历左子树
    postOrderTraversal(node->left);

    // 遍历右子树
    postOrderTraversal(node->right);

    // 计算当前结点的平衡因子，并输出
    node->balanceFactor = calculateBalanceFactor(node);//平衡因子=左子树高度-右子树高度
    cout << node->data << " " << node->balanceFactor << endl;
}



int main() {
    int t;
    cin >> t;

    for (int i = 0; i < t; ++i) {
        int n;
        cin >> n;

        char* treeArray = new char[n];
        for (int j = 0; j < n; ++j) {
            cin >> treeArray[j];//这里不再用插入的做法进行建树
        }

        // 构建二叉树
        TreeNode* root = nullptr;
        TreeNode* nodes = new TreeNode[n];
        for (int j = 0; j < n; ++j) {
            if (treeArray[j] == '0')continue;//遇到0则过
            nodes[j] = TreeNode(treeArray[j]);//给结点初始化

            //从第二个结点开始分左右建
            if (j > 0) {
                //parent指针记录结点的爹，由于是数组的形式，所以可以用（j-1）/2表示
                int parent = (j - 1) / 2;
                //左孩子是2*k+1，右孩子是2*k+2
                if (j % 2 == 1) {//若余数为1说明是他爹的左孩子
                    nodes[parent].left = &nodes[j];
                }
                else {//否则就是他爹的右儿子
                    nodes[parent].right = &nodes[j];
                }
            }
            else {
                //第一个结点直接扔进去
                root = &nodes[j];
            }
        }
        // 后序遍历并输出平衡因子
        postOrderTraversal(root);

        delete[] treeArray;
        delete[] nodes;
    }

    return 0;
}